Частина 2
КИЇВ КНУТД 2013
Моделювання електромеханічних систем: методичні вказівки до виконання лабораторних занять та самостійної роботи для студентів усіх форм навчання напряму 6.050702 «Електромеханіка». Частина 2 / упор.: Т.Я. Біла – К.: КНУТД, 2013. – 71 с.
Упорядник: Біла Тетяна Яківна, к. т. н., доцент.
Відповідальний за випуск: Злотенко Б. М., д. т. н., професор.
Затверджено на засіданні кафедри електромеханічних систем.
Протокол № 9 від 26.02.2013 р.
ЛАБОРАТОРНЕ ЗАНЯТТЯ № 3
Тема «Моделювання електромеханічних пристроїв
у режимі статики»
Мета заняття: одержати практичні навички складання і аналізу математичних
моделей на макрорівні засобами MatLab за усталених режимах
роботи.
Завдання 1. Визначити реакції в опорах балки, навантаженої різними силовими факторами, при плоскому поперечному вигині.
Послідовність виконання
1. Накреслити згідно з варіантом схему навантаження балки в зошиті для лабораторних занять.
2. Показати на схемі реакції в опорах і позначити їх RA та RB.
3. Скласти систему лінійних алгебраїчних рівнянь для визначення реакцій в опорах у канонічній формі.
4. Створити у командному вікні програми MatLab заголовок лабораторного заняття, указавши варіант завдання.
5. Ввести задані значення параметрів схеми.
6. Знайти рішення засобами MatLab. Занести в протокол лабораторного заняття отриманні значення.
7. Виконати перевірку отриманих значень реакцій в опорах.
8. Файл зберегти як документ Word.
Варіанти завдань
1)
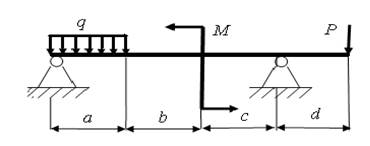
а = 2,2 м; b = 3,4 м; с = 1,9 м; d = 2,5 м; Р = 19 кН; q = 21 кН/м; M = 7 кН.
2)
а = 2,4 м; b = 3,6 м; с = 2 м; d = 3 м; Р = 18 кН; q = 20 кН/м; M = 8 кН.
3)
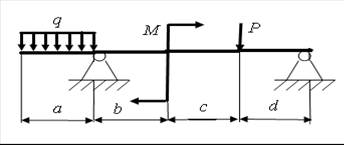
а = 2,6 м; b = 3,8 м; с = 2,1 м; d = 2,5 м; Р = 16 кН; q = 19 кН/м; M = 8 кН.
4)
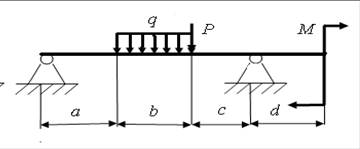
а = 2,8 м; b = 4 м; с = 2 м; d = 3,2 м; Р = 15 кН; q = 18 кН/м; M = 9 кН.
5)
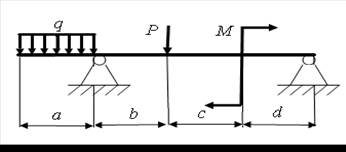
а = 3 м; b = 4,2 м; с = 2,3 м; d = 2,5 м; Р = 14 кН; q = 17 кН/м; M = 9 кН.
6)
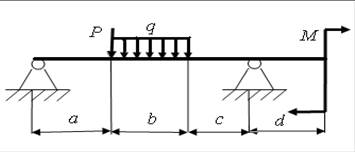
а = 3,2 м; b = 4,4 м; с = 2,4 м; d = 3 м; Р = 13 кН; q = 16 кН/м; M = 10 кН.
7)
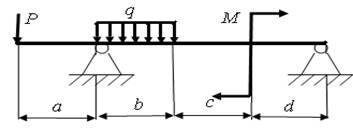
а = 3,4 м; b = 4,6 м; с = 2,5 м; d = 2,5 м; Р = 12 кН; q = 15 кН/м; M = 10 кН.
8)
а = 3,6 м; b = 4,8 м; с = 2,6 м; d = 2 м; Р = 11 кН; q = 14 кН/м; M = 11 кН.
9)
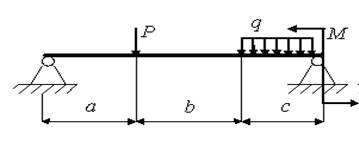
а = 1 м; b = 1,5 м; с = 1,5 м; Р = 4,0 кН; q = 1,2 кН/м; M = 2,5 кН.
10)
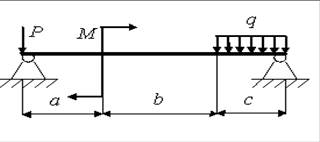
а = 1,5 м; b = 1 м; с = 2 м; Р = 3,0 кН; q = 1,5 кН/м; M = 2,0 кН.
11)
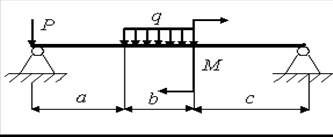
а = 2,0 м; b = 1,0 м; с = 2,0 м; Р = 2,5 кН; q = 1,6 кН/м; M = 1,5 кН.
12)
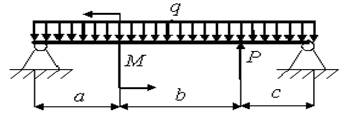
а = 1,0 м; b = 1,6 м; с = 2,0 м; Р = 2,0 кН; q = 1,4 кН/м; M = 3,0 кН.
13)
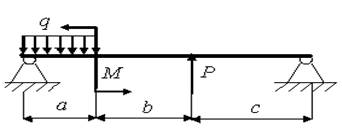
а = 1,2 м; b = 1,4 м; с = 1,6 м; Р = 4,0 кН; q = 1,0 кН/м; M = 2,5 кН.
14)
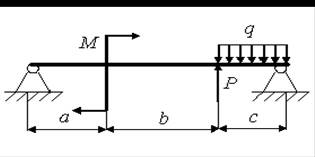
а = 1,0 м; b = 2,5 м; с = 1,5 м; Р = 3,5 кН; q = 2,0 кН/м; M = 2,0 кН.
15)
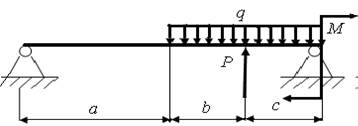
а = 2,0 м; b = 1,0 м; с = 2,0 м; Р = 2,0 кН; q = 2,0 кН/м; M = 3,0 кН.
16)
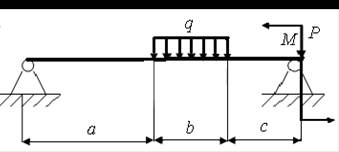
а = 1,6 м; b = 2,0 м; с = 1,2 м; Р = 1,0 кН; q = 1,8 кН/м; M = 2,0 кН.
17)
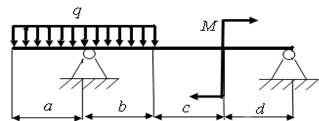
а = 4,6 м; b = 4,4 м; с = 2,0 м; d = 4 м; q = 10 кН/м; M = 10 кН.
18)
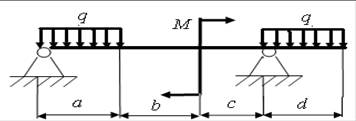
а = 4,2 м; b = 2,2 м; с = 3,8 м; d = 6,8 м; q = 20 кН/м; M = 20 кН.
19)
а = 4 м; b = 2,4 м; с = 4,0 м; d = 3,6 м; Р = 3 кН; q = 3,5 кН/м; M = 4 кН.
20)
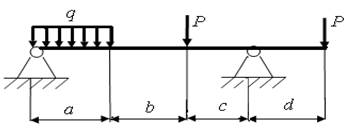
а = 3,8 м; b = 2,8 м; с = 4,4 м; d = 5 м; Р = 5 кН; q = 5 кН/м.
21)
а = 3,6 м; b = 3 м; с = 4 м; d = 2,4 м; Р = 7 кН; q = 22 кН/м.
22)
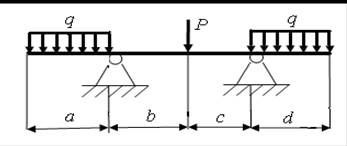
а = 3,4 м; b = 3,6 м; с = 3,6 м; d = 4,4 м; Р = 9 кН; q = 4 кН/м.
23)
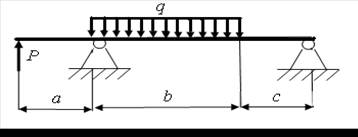
а = 3,2 м; b = 3,4 м; с = 3,4 м; Р = 8 кН; q = 8 кН/м.
24)
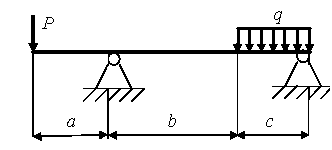
а = 3 м; b = 3,0 м; с = 2 м; Р = 12 кН; q = 2 кН/м.
25)
а = 0,6 м; b = 1,1 м; с = 0,7 м; Р = 2,2 кН; q = 1,5 кН/м; M = 1,3 кН.
26)
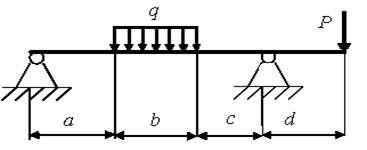
а = 2,4 м; b = 1,6 м; с = 2,6 м; d = 1,4 м; Р = 5 кН; q = 4,7 кН/м.
27)
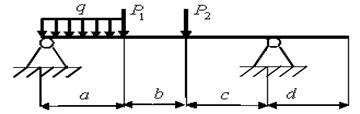
а = 0,7 м; b = 0,6 м; с = 0,8 м; d = 0,4 м; Р1 = 7 кН; P2 = 10 кН; q = 1,7 кН/м.
28)
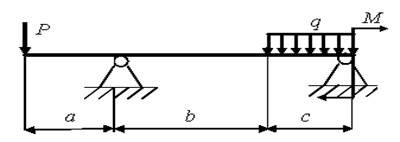
а = 1,3 м; b = 2,1 м; с = 1,4 м; Р = 1,2 кН; q = 2,5 кН/м; M = 2,7 кН.
29)
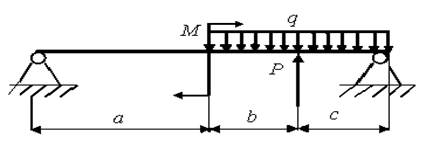
а = 2,5 м; b = 1,1 м; с = 2,1 м; Р = 2,4 кН; q = 1,5 кН/м; M = 0,9 кН.
30)
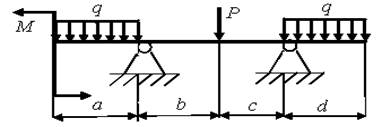
а = 4 м; b = 2,4 м; с = 3,2 м; d = 2,6 м; Р = 5 кН; q = 5,5 кН/м; M = 2 кН.
Завдання 2. Розрахувати задане багатоконтурне коло на постійному струмі методом контурних струмів.
Послідовність виконання
1. Накреслити згідно з варіантом електричну схему в зошиті для лабораторних занять.
2. Показати на схемі обраний напрямок струмів в кожному контурі, позначити їх І1k, І2k … Іnk (n – кількість контурів).
3. Скласти систему лінійних алгебраїчних рівнянь у канонічній формі для визначення значень контурних струмів.
4. Створити у командному вікні програми MatLab заголовок лабораторного заняття, указавши варіант завдання.
5. Ввести задані значення параметрів схеми (таблиця).
6. Знайти рішення засобами MatLab. Занести в протокол лабораторного заняття отриманні значення.
7. Визначити значення струмів на кожному елементі (гілці) електричного кола.
8. Виконати перевірку отриманих значень за першим законом Кірхгофа.
9. Файл зберегти як документ Word.
Варіанти завдань електричної схеми
1)
2)
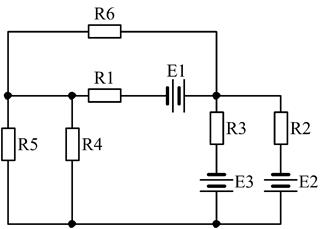
3)
4)
5)
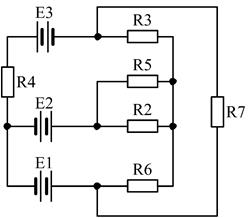
6)
7)
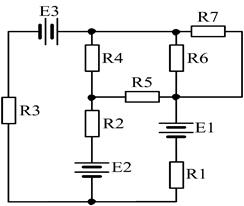
8)
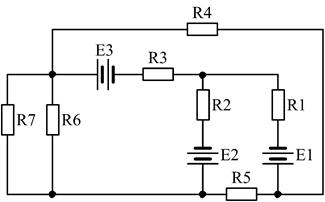
9)
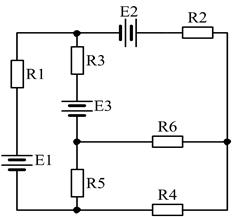
10)
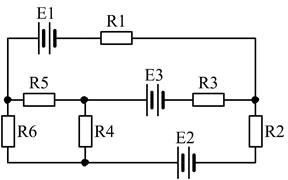
11)
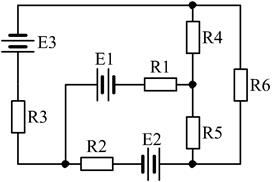
12)
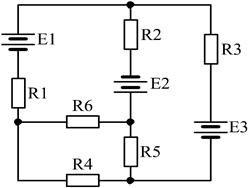
13)
14)
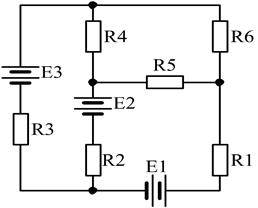
15)
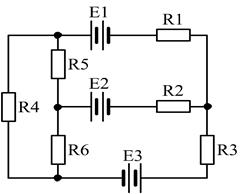
16)
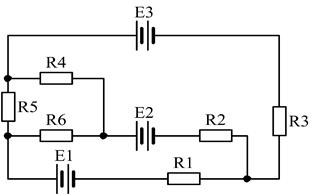
17)
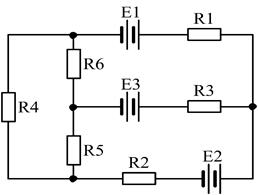
18)
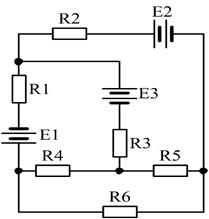
19)
20)
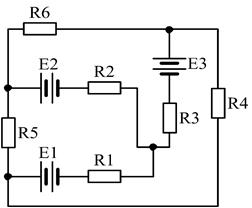
21)
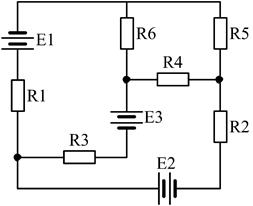
22)
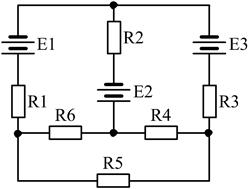
23)
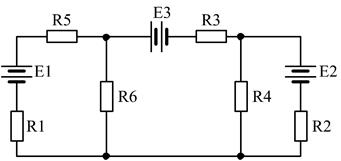
24)
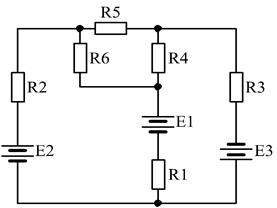
25)
26)
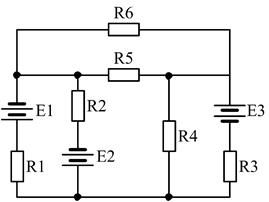
27)
28)
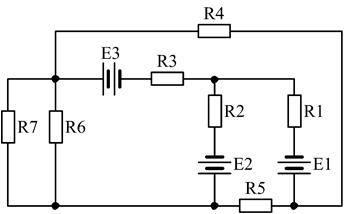
29)
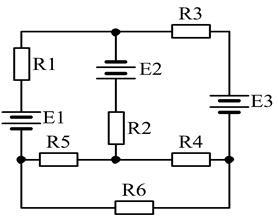
30)
Таблиця
Значення параметрів електричних схем
| Вар | Е1,.,Е3, В | R1,.,R7, Ом | Вар | Е1,.,Е3, В | R1,.,R7, Ом |
| 36, 10, 25 | 4, 8, 3, 1, 2, 7 | 5, 16, 30 | 6, 4, 3, 2, 5, 3 | ||
| 6, 20, 4 | 4, 6, 4, 4, 3, 3, 1.2 | 21, 4, 10 | 5, 7, 2, 8, 1, 1 | ||
| 4, 24, 6 | 0, 8, 1, 6, 10, 4, 1.2 | 72, 12, 4 | 6, 1, 10, 4, 12, 4, 6 | ||
| 12, 48, 6 | 2.5, 1, 4, 15, 2, 2, 4 | 12, 30, 25 | 1, 5, 1, 1, 6, 4, 6 | ||
| 22, 24, 10 | 2, 1, 8, 4, 10, 6 | 55, 18, 4 | 8, 4, 3, 2, 4, 4 | ||
| 5, 16, 30 | 6, 4, 3, 2, 5, 3 | 10, 6, 24 | 3.5, 5, 6, 6, 3, 1 | ||
| 21, 4, 10 | 5, 7, 2, 8, 1, 1 | 4, 9, 18 | 2.7, 10, 4, 8, 10, 2 | ||
| 4, 24, 6 | 9, 8, 1, 6, 10, 4 | 16, 8, 9 | 2.5, 6, 6, 5, 10, 5 | ||
| 12, 6, 40 | 2, 3, 8, 5, 7, 8 | 12, 48, 6 | 2.5, 1, 4, 15, 2, 2 | ||
| 12, 30, 9 | 3.5, 2, 3, 3, 1, 3 | 9, 6, 27 | 4.5, 2, 8, 13, 4, 3 | ||
| 15, 63, 6 | 5, 3, 1, 2, 12, 3 | 36, 9, 24 | 3, 4, 2, 1, 5, 1 | ||
| 10, 32, 10 | 1.5, 6, 1, 7, 1, 5 | 5, 10, 36 | 1.2, 6, 3, 2, 2, 2 | ||
| 20, 30, 40 | 7, 3, 5, 10, 4, 3.7 | 35, 25, 15 | 5.4, 8, 4.1, 6, 1, 7 | ||
| 10,25, 45 | 9, 2, 8, 4, 7, 3, 5 | 22, 17, 12 | 5, 3, 9, 6, 7, 1, 4 | ||
| 5,17, 9 | 8, 3, 4, 9, 5.7, 6 | 34, 14, 21 | 10, 5, 7, 2, 6.7, 8 |
Контрольні питання
1. Які Ви знаєте способи побудови моделей за усталених режимах роботи?
2. Які Ви знаєте способи рішення системи лінійних алгебраїчних рівнянь за допомогою програми MatLab?
3. Приведіть послідовність виконання завдання 1.
4. Як визначаються реакції в опорах?
5. Як перевірити правильність їхнього розрахунку?
6. Наведіть умови рівноваги механічної системи.
7. Приведіть послідовність виконання завдання 2.
8. Опишіть алгоритм формування математичного опису електричного кола за методом контурних струмів.
9. У яких випадках значення струмів на елементах відрізняються від значень контурних струмів?
10. Яким чином розраховуються струми на елементах?
11. Сформулюйте сутність метода контурних струмів.
12. Як перевірити правильність розрахунків струмів на елементах?
13. Наведіть умови рівноваги електричної системи.
14. Чому чисельні методи рішення систем лінійних рівнянь являються ітераційними?
15. Яким чином оголошуються змінні мовою MatLAB?
16. Як зробити, щоб результат дій, які записані у черговий рядок виводився до командного вікна або не виводився на екран?
17. Як ввести кілька операторів одним рядком?
18. Яку роль виконує системна змінна ans?
19. Як вводяться вектори у мові MatLAB?
20. Як ввести у командне вікно пояснювальний текст?
21. Яким чином можна звернутись до окремого елемента вектора?
22. Який розмір має матриця А коефіцієнтів системи лінійних рівнянь?
23. Який розмір повинен бути у вектора В правої частини системи лінійних рівнянь?
24. Які знаки мають елементи головної діагоналі матриці А коефіцієнтів системи лінійних рівнянь?
25. Наведіть узагальнений алгоритм рішення систем лінійних рівнянь за допомогою комп’ютерних програм.
Теоретичні відомості до лабораторного заняття № 3
Загальні поняття процесу аналізу математичних моделей в режимі статики
Постановка задач аналізу статичних режимів. Існує два підходи до аналізу статичних станів технічних об’єктів.
Перший підхід використовує в якості математичної моделі об’єкта систему звичайних диференційних рівнянь (ЗДР)
;
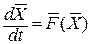де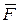 
- k –мірний вектор-функція (сукупність функцій f1, f2,…,fk); 
- k - мірний вектор аргументів; t – час.
Рішення цієї системи виконується з врахуванням того, що статичний режим є граничним, до якого прямують перехідні процеси під час затухання, тобто при t→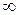 
. Точка, в якій 
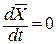, і буде точкою рішення 
системи в статичному режимі.
Якщо об’єкт багатостабільний (має більш одного стійкого стану), рішення задачі аналізу статики неоднозначно. Тоді чисельне інтегрування системи диференційних рівнянь дає одне з можливих рішень. Отримання інших стаціонарних точок можливе повторенням рішення за інших векторах початкових умов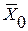 
.
Другий підхід до аналізу статики більш економічний. В цьому випадку в якості математичної моделі об’єкта приймається система лінійних алгебраїчних або нелінійних трансцендентних рівнянь
.
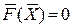Такі рівняння можна одержати з системи диференційних рівнянь, які описують перехідні процеси в електричній або механічній системах, якщо врахувати, що в статичному режимі диференціали (похідні) дорівнюють нулю.
Методи рішення задач статики. Розглянуті підходи розрізняються за своєю постановкою, але методи рішення систем рівнянь, які використовуються в них, об’єднує те, що всі вони ітераційні та ґрунтуються на використання формули
;
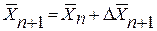де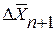 
- поправка вектора на (n +1) – й ітерації.
Ітераційний процес слід припиняти після того, як поточна точка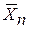 
виявиться в заданому ε – просторі стаціонарної точки , тобто
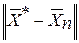< ε;
де 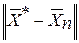- норма вектора нев’язок 
.
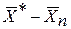Системи нелінійних рівнянь вирішуються чисельними методами простих ітерацій, Ньютона, порозрядного або подекадного наближень, системи лінійних рівнянь – методом Гауса, обертання. Для рішення складаються програми, що реалізують обраний чисельний метод, мовами QBasic, Pascal та іншими.
Узагальнений алгоритм рішення систем лінійних алгебраїчних рівнянь за допомогою комп’ютерних прикладних програм. Для знаходження рішення моделі об’єкта за усталеним режимом роботи на персональному комп’ютері система лінійних рівнянь (яка і є моделлю) повинна бути представлена в канонічній форми і має загальний вигляд
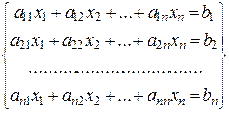
або в матричній формі
А · Х = В;
де n – кількість рівнянь (дорівнює кількості невідомих); А – матриця розміром [ n x n ] коефіцієнтів при невідомих лівої частини рівнянь; Х – вектор невідомих довжиною [ n x 1]; В – вектор правої (відомої) частини системи рівнянь довжиною [ n x 1]; тобто в розгорнутому вигляді
; 
; 
.
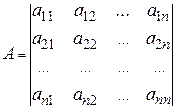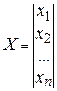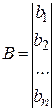Для рішення засобами комп’ютерних програм необхідно: по-перше, ввести значення параметрів моделі, які визначають коефіцієнти матриці А; по-друге, ввести матрицю А, вектор В; по-третє, знайти рішення (тобто вектор Х) за допомогою спеціальних операторів чи вбудованих функцій, які використовуються в обраній програмі для рішення системи лінійних алгебраїчних рівнянь.
Приклад виконання завдання 1
Необхідно визначити реакції в опорах балки, схема навантаження якої наведена на рис. 1, якщо а = 0,8 м; b = 0,6 м; Р = 10 кН.
Позначимо реакції в опорах через RA та RB. Невідомі реакції опор визначають за правилами механіки з умов рівноваги пласкої системи сил.
Рисунок 1 – Розрахункова схема до приклада 1
Складаємо математичний опис за рівняннями рівноваги балки:
1) Σ Y = 0 – алгебраїчна сума проекцій всіх сил на вісь координат У дорівнює нулю;
2) Σ MA = 0 – сума моментів відносно точки А дорівнює нулю.
RA + RB – P = 0; - P · a + RB · (a + b) = 0.
Представимо рівняння в канонічній формі
.
Для перевірки отриманих значень можна використати рівняння Σ MВ = 0 – сума моментів відносно точки В дорівнює нулю:
RA · (a + b) - P · b = 0.
Підготуємо до рішення в командному вікні програми MatLab:
; 
; 
.
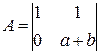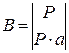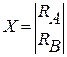Наведемо текст програми рішення в командному вікні з врахуванням узагальненого алгоритму.
>> %Лабораторне заняття № 3
>> %Визначення реакцій в опорах балки
>> %Введення параметрів балки
>> a=0.8;b=0.6;P=10;
>> %Введення матриці коефіцієнтів при невідомих А
>> A=[1 1;0 a+b]
A =
1.0000 1.0000
0 1.4000
>> %Введення вектора правої частини системи рівнянь В
>> B=[P;P*a]
B =
>> %Пошук рішення системи лінійних рівнянь Х
>> X=A\B
X =
4.2857
5.7143
>> %Присвоєння отриманим значенням вектора Х позначень Ra та Rb
>> Ra=X(1)
Ra =
4.2857
>> Rb=X(2)
Rb =
5.7143
>> %Виконання перевірки отриманих значень
>> Ra*(a+b)-P*b
ans =
-8.8818e-016
>> %Висновок: реакції знайдено правильно.
