Система плоскостей линейной перспективы

При рассмотрении метода линейной перспективы следует различать следующие основные точки, линии, плоскости и части пространства (рис.73):

S – точка зрения (центр проецирования);

S₁ – основание точки зрения (точка стояния);

P – главная точка стояния;

P₀ – основание главной точки картины;

П₁ – предметная плоскость;

П^/ - картинная плоскость;

Г – плоскость горизонта;

N – плоскость, параллельная П^/ и проходящая через точку S, - нейтральная

Плоскость;

O₁ – O₂ – основание картины;

h – h – линия горизонта;

S – P – главный луч картины ;

d – главное расстояние;

H – высота горизонта.

Пространство до плоскости N называется мнимым, между плоскостями N и П^/ – промежуточным, а за плоскостью П^/ – предметным.

Для построения перспективы необходимо знать положение точки S относительно плоскостей П^/ и П₁.

ПЕРСПЕКТИВЫ ТОЧЕК, РАСПОЛОЖЕННЫХ В РАЗЛИЧНЫХ

ЧАСТЯХ ПРОСТРАНСТВА.

Рассмотрим точку А в предметном пространстве и проследим за тем, как будут изменяться положения ее перспективы А^/ и вторичной проекции А₁^/ при движении точки А вдоль проецирующего луча SA (рис.74).

Из рис. 74 видно, что положение точки в той или иной части пространства относительно плоскости картины П^/ определяется положением ее вторичной проекции в плоскости картины П^/ относительно линии горизонта h – h и линии основания картины O₁ – O₂.

Вторичная проекция бесконечно удаленной точки предметного пространства (точка F) должна находиться на линии горизонта (линии h – h).

Если точки равноудалены от плоскости картины, то их вторичные проекции находятся на одинаковом расстоянии от основания картины (линии O₁ – О₂).

		Рис. 74. Перспективы и вторичные проекции точек, расположенных в разных частях пространства: F – бесконечно удаленная точка предметного пространства; А и В – точки, находящиеся в предметном пространстве; R – точка, лежащая в предметной плоскости; М – точка, лежащая в плоскости картины; L – точка, лежащая в промежуточном пространстве; К - точка, лежащая в мнимом пространстве.

При удалении точки, находящейся в предметном пространстве, от плоскости картины П^/ расстояние от ее вторичной проекции А₁^/ до основания картины

(линии O₁ – O₂) увеличивается, а вторичные проекции точек находятся между основанием картины (линией O₁ – O₂) и линией горизонта картины h – h (точки А и В).

Вторичные проекции точек, расположенных в промежуточном пространстве (точка L), находятся ниже основания картины (линии O₁ – O₂), а расположенных в мнимом пространстве (точка К) – выше линии горизонта.

Вторичная проекция точки, лежащей в плоскости картины П^/ (точка М), находится на основании картины (линии O₁ – O₂).

На основе изложенного материала могут решаться прямые и обратные задачи по построению наглядного изображения (изображение в косоугольной фронтальной диметрической аксонометрической проекции) положения точки в пространстве или ее перспективы и вторичной проекции.

Пример 7. Построить положение точек A, B, C и D в пространстве по заданным их перспективам и вторичным проекциям (прямая задача) и построение перспектив и вторичных проекций по заданному положению точек (обратная задача) (рис. 75).

		Рис. 75. Построение положения точек по заданным их перспективам и вторичным проекциям.

Алгоритм решения задач следующий. Сначала задается положение предметной плоскости П₁ и плоскости картины П^∕, строится линия начала картины(О₁ – О₂). По заданным параметрам высоты горизонта H и главного расстояния d строится положение точки зрения S относительно плоскости картины П^∕ и предметной плоскости П₁. Строятся основание точки зрения S₁, линия горизонта (h - h), главная точка картины P и основание главной точки картины P₀.

- прямая задача (на примере построения точки А) (см. рис. 75).

1. Линия проекционной связи проекций А^∕ и А^∕₁ продлевается в плоскости картины П^∕ до пересечения с линией начала картины (О₁ – О₂) и через полученную точку А₀ и точку стояния S₁ проводимслед лучевой проецирующей плоскости;

2. Через точку зрения S и вторичную проекцию точки А^∕₁ проводится луч до пересечения с продолжением линии (А₀ - S₁): полученная точка пересечения А₁ – это проекция точки А на предметной плоскости;

3. Точка А найдется на пересечении луча (S - А^∕) с вертикальной линией проекционной связи из точки А₁;

- обратная задача (на примере построения точки В) (см. рис. 75).

1. Из точки В опускается вертикальная линия проекционной связи на предметную плоскость П₁ – получаем проекцию точки на предметной плоскости В₁. Проводим след лучевой проецирующей плоскости через точки В₁ и S₁;

2. В точке пересечения линии (В₁ - S₁) с линией начала картины (О₁ – О₂) получаем точку В₀ – проекцию перспективы и вторичной проекции точки В на линии начала картины (О₁ – О₂). Из точки В₀ в плоскости картины П^∕ восстанавливаем вертикальную линию проекционной связи;

3. Перспектива точки В^∕ найдется в точке пересечения вышеуказанной линии проекционной связи с лучом (S - В), а вторичная проекция В^∕₁ - с лучом (S – В₁).

ПЕРСПЕКТИВА ПРЯМОЙ ЛИНИИ.

 

Перспективное изображение прямой обратимо, если оно дополнено вторичной проекцией. На рис.76 перспектива прямой АВ и ее вторичная проекция определены перспективами и вторичными проекциями двух ее точек А и В.

 

 

Имея А^/В^/ и А₁^/ В₁^/, можно определить две характерные точки прямой:

F^/ - перспектива бесконечно удаленной точки F, принадлежащей прямой АВ; F^/ находится на пересечении линии проекционной с из F^/ с продолжением прямой А^/В^/ (вторичная проекция F₁^/ точки F находится как точка пересечения А₁^/ В₁^/ с линией горизонта h – h);

N^/ - перспектива начала прямой (началом прямой принято называть точку пересечения прямой с плоскостью картины); N^/ находится на пересечении линии проекционной с из N^/ с продолжением прямой А^/В^/ (вторичная проекция N₁^/ точки N находится как точка пересечения А₁^/ В₁^/ с линией начала картины O₁ –O₂).

Точками F^/ и N^/ обычно пользуются при построении перспективы различных предметов.

Рис. 69. Положения прямой в пространстве: а – нисходящая прямая; б – восходящая прямая; в – горизонтальная прямая; г – прямая, перпендикулярная плоскости картины; д – прямая, перпендикулярная предметной плоскости; е – прямая, параллельная плоскости картины; ж – прямая, параллельная плоскости картины и предметной плоскости

Положение перспективы несобственной точки прямой на картине (F^/) позволяет судить о положении прямой в пространстве (рис.77):

если точка F^/ оказалась над линией горизонта, то прямая – восходящая

(рис.77, а);

- если точка F^/ оказалась под линией горизонта, то прямая – нисходящая

(рис.77, б);

- - если точка F^/ находится на линии горизонта, то прямая расположена горизонтально, параллельно предметной плоскости П₁ (рис.77, в);

- если точка F^/ совпадает с главной точкой картины (Р), то прямая перпендикулярна плоскости картины П^/ (рис.77, г);

- в том случае, когда прямая перпендикулярна предметной плоскости (П₁) ее вторичная проекция становится точкой (рис.77, д);

- когда прямая параллельна плоскости картины (П^/), ее вторичная проекция параллельна основанию картины(O₁ –O₂) (рис.77, е).

Пример 8. По положению перспектив и вторичных проекций конечных точек А и В отрезка построить положение прямой АВ в пространстве. Построить характерные точки прямой: начало прямой N и точку схода прямой F (рис.78).

	Рис. 78. Построение положения прямой AB и ее характерных точек: N – начала прямой и F – бесконечно удаленной точки прямой по заданным перспективам и вторичным проекциям конечных точек отрезка.

Алгоритм решения задачи. Задается положение предметной плоскости П₁ и плоскости картины П^∕, строится линия начала картины (О₁ – О₂). По заданным параметрам высоты горизонта H и главного расстояния d строится положение точки зрения S относительно плоскости картины П^∕ и предметной плоскости П₁. Строятся основание точки зрения S₁, линия горизонта (h - h), главная точка картины P и основание главной точки картины P₀.

1. По алгоритму решения задачи, приведенному в предыдущем примере (см. рис.77), строятся точки А и В и прямая АВ;

2. Соединив перспективы точек А^∕ и В^∕ получаем перспективу прямой А^∕В^∕, а соединяя вторичные проекции точек А^∕₁ и В^∕₁ получаем вторичную проекцию прямой А^∕₁В^∕₁;

3. Продолжив вторичную проекцию прямой А^∕₁В^∕₁ до пересечения с линией начала картины

(О₁ – О₂), получаем вторичную проекцию начала прямой N^∕₁. Перспектива начала прямой N^∕ найдется как точка пересечения вертикальной линии проекционной связи из точки N^∕₁ с продолжением перспективы прямой А^∕В^∕. Точка начала прямой N как точка, лежащая в плоскости картины, совпадает с ее перспективой N ≡ N^∕;

4. Продолжив вторичную проекцию прямой А^∕₁В^∕₁ до пересечения с линией горизонта

(h – h), получаем вторичную проекцию бесконечно удаленной точки прямой F^∕₁. Перспектива бесконечно удаленной точки прямой F^∕ найдется как точка пересечения вертикальной линии проекционной связи из точки F^∕₁ с продолжением перспективы прямой А^∕В^∕. Бесконечно удаленная точка прямой F как точка, лежащая в плоскости картины, совпадает с ее перспективой F ≡ F^∕;

5. Правильность и корректность выполненных построений проверяется следующим образом:

- прямая АВ в своем продолжении обязательно должна пройти через точку N;

- прямая, проведенная через точки S и F, должна быть параллельна построенной прямой АВ;

6. Если конечные точки прямой лежат в предметной части пространства или в промежуточном пространстве, то перспектива и вторичная проекция прямой выполняются сплошными основными линиями, проводимыми соответственно между перспективами и вторичными проекциями конечных точек прямой (см. рис. 78);

7. Если одна из точек прямой расположена в мнимом пространстве, то перспектива и вторичная проекция прямой выполняются сплошными основными линиями, которые начинаются соответственно вперспективах и вторичных проекциях конечных точек прямой и выполняются как расходящиеся в противоположные стороны отрезки, лежащими соответственно на линиях А^∕В^∕ и А^∕₁В^∕₁ (см. рис. 79). Правомочность данного утверждения доказывается построением перспектив и вторичных проекций точек K и L, лежащих на прямой АВ (обратная задача). При этом соответственно точки А^∕ и В^∕, и А^∕₁ и В^∕₁ между собой соединяются сплошной тонкой линией вспомогательных построений.

 

 

 

 

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ

Параллельные прямые

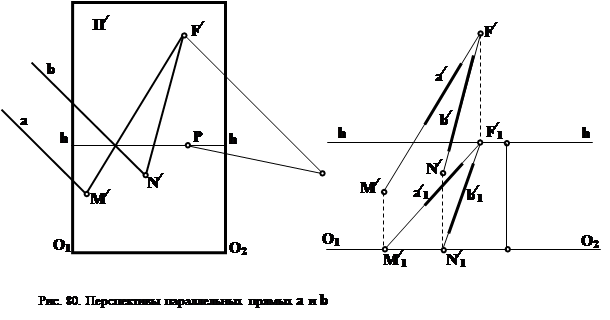
Перспективы параллельных прямых пересекаются. Точка пересечения связки параллельных прямых называется точкой схода (см. точку F^/ на

рис. 80).

Точка схода горизонтальных параллельных прямых лежит на линии горизонта (рис.81, а).

Если горизонтальные параллельные прямые перпендикулярны к плоскости картины (П ^/), то точкой схода их служит главная точка картины (Р) (рис.81, б).

Точка схода параллельных прямых, лежащих в предметной плоскости П₁,

находится на линии горизонта (рис.81, в).

Перспективы и вторичные проекции параллельных прямых параллельны, если прямые параллельны плоскости картины (П ^/) (рис.82).