Взаимно перпендикулярные плоскости, изображенные на рис. 6, дают нам пространственный чертеж. Для получения всех трех проекций точки в одной плоскости чертежа все три плоскости проекций p1, p2 и p3 условно совмещают с плоскостью чертежа. Это совмещение выполняется следующим образом.
Фронтальная плоскость проекций p2 принимается за плоскость чертежа, горизонтальная плоскость проекций p1 совмещается с плоскостью чертежа вращением вокруг оси x, а профильная плоскость проекций p3 - вращением вокруг оси z. Направление вращения на рис. 6, а показано стрелками.
При совмещении плоскости p1 с плоскостью чертежа положительное направление оси y совмещается с отрицательным направлением оси z, а отрицательное направление – с положительным направлением оси z. На чертеже изображение этой оси y принято обозначать y p1(рис. 6, б).
При совмещении плоскости p3 с плоскостью чертежа положительное направление оси y совмещается с отрицательным направлением оси x, а отрицательное направление – с положительным направлением оси x. На чертеже изображение этой оси y принято обозначать y p3.
В результате образуется ортогональный чертеж или эпюр (от франц. epure - чертеж, проект).На эпюре изображаются только проекции геометрических объектов, а не сами объекты.
Любые две проекции точки, изображенные на эпюре, связаны между собой линией проекционной связи, перпендикулярной оси проекций (на чертеже она обозначается штриховой линией):
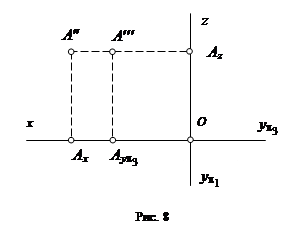
- горизонтальная и фронтальная проекции (точки А ¢ и А ²) расположены на линии проекционной связи, перпендикулярной оси x;
- фронтальная и профильная проекции (точки А ² и А ¢¢¢) - на линии проекционной связи, перпендикулярной оси z;
- горизонтальная и профильная проекции (точки А ¢ и А ¢¢¢) - на линии проекционной связи, перпендикулярной оси y.
Вследствие того, что отрезки ОАy p1и OАy p3являются изображением одной и той же координаты yA, точки Аy p1и Аy p3связывают дугой окружности с центром в начале координат.
Каждая проекция точки А определяется двумя координатами:
- горизонтальная проекция А ¢(xA; yA);
- фронтальная проекция А ² (xA; zA);
- профильная проекция А ¢¢¢ (yA; zA).
Положение точки А может быть задано как графически, так и аналитически. Пример графического изображения точки А рассмотрен нами на рис. 6. Аналитическая форма задания точки представляет собой числовое выражение трех координат точки А, измеряемое в выбранных единицах длины (например, запись А (3;2;3) означает, что xA =3, yA =2, zA =3).
От аналитической формы задания точки легко перейти к графическому изображению этой точки на ортогональном чертеже.


 Пример 1. Построить проекции точки
Пример 1. Построить проекции точки
В (-2;-3;1).
1. Выбираем единичный отрезок (рис.7).
2. С учетом знака откладываем на осях проекций координатные отрезки
xВ = | ОВх | = -2;
yВ = | ОВyp1 | = | ОВy p3| = -3;
zВ = | ОВz | = 1.
3. Отмечаем точки Вx, Вy p1, Вy p3, Вz.
4. Из построенных точек Вx, Вyp1, Вyp3, Вz проводим линии проекционной связи, перпендикулярные осям проекций, и на их пересечениях отмечаем проекции точки В:
В ¢ = (ВxВ ¢ ^ x) Ç (Вy p1 В ¢ ^ y p1);
В ¢¢ = (ВxВ ¢¢ ^ x) Ç (ВzВ ¢¢ ^ z);
В ¢¢¢ = (Вy p3 В ¢¢¢ ^ y p3) Ç (ВzВ ¢¢¢ ^ z).
Две проекции точки, построенные на эпюре, однозначно определяют ее положение в пространстве. По двум проекциям заданной точки можно построить третью, и притом только одну.