С квадратной матрицей коэффициентов и ее решение
По правилу Крамера
Рассмотрим систему линейных уравнений из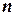 
уравнений с 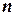неизвестными:
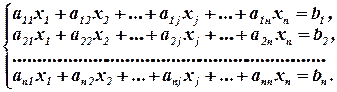
Матрица коэффициентов при неизвестных содержит 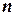строк и 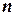столбцов:
Теорема Крамера. Если определитель 
отличен от нуля, то рассматриваемая система линейных уравнений определенная и ее единственное решение находится по формулам:
где
- определитель, полученный из определителя заменой 
- ого столбца, т.е. столбца коэффициентов при неизвестной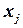 
, на столбец свободных членов.
▼
Пример
Решить систему, заданную расширенной матрицей:
Решение.
Ответ:
▲
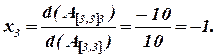
Обратная матрица и ее вычисление
Решить систему линейных уравнений с квадратной матрицей коэффициентов можно и другим способом, используя обратную матрицу. При этом определитель матрицы коэффициентов должен быть также отличен от нуля.
Рассмотрим квадратную матрицу:
Вырожденной (особенной) называется квадратная матрица, если ее определитель равен нулю, и невырожденной (неособенной) – в противном случае.
Обратной для матрицы 
называется матрица 
если выполняется:
где
единичная матрица.
Для вырожденной матрицы обратной матрицы не существует.
Обратную матрицу можно вычислить разными способами.
А) Одно из правил вычисления обратной матрицы:
1) берется невырожденная матрица 
2) обратная матрица 
находится по формуле
где 
присоединенная (или взаимная) матрица, состоящая из алгебраических дополнений 
элементов 
матрицы , где 
- минор порядка 
матрицы , получаемый из определителя матрицы вычеркиванием 
-ой строки и -ого столбца.
Обратим внимание, что в присоединенной матрице строки транспонированы в столбцы.
▼
Пример
Вычислить обратную матрицу для матрицы:
.
Решение.
Вычислим определитель матрицы: 
.
Определитель матрицы 
отличен от нуля, следовательно, для матрицы существует единственная обратная матрица. Вычислим присоединенную матрицу:
, 
, 
, 
,
.
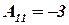Проверкой убеждаемся, что 
.
▲
Б) Обратную матрицу можно вычислить после элементарных преобразований (преобразований Жордана-Гаусса) над строками матрицы:
1) умножение (деление) строки матрицы на любое число, отличное от нуля;
2) прибавление к одной строке матрицы другой строки, умноженной на любое число.
Для того, чтобы вычислить обратную матрицу для матрицы 
, необходимо составить матрицу 
, затем с помощью элементарных преобразований преобразовать матрицу к виду единичной матрицы 
, тогда на месте единичной матрицы получим матрицу :
.
▼
Пример
Вычислить обратную матрицу для матрицы
.
Решение.
Составим матрицу вида:
.
Элемент 
и первую строку, содержащую данный элемент, назовем направляющими. Осуществим элементарные преобразования, в результате которых первый столбец преобразуется в единичный с единицей в первой строке. Для этого к второй и третьей строкам прибавим первую строку, соответственно умноженную на 1 и –2. В результате данных преобразований получим матрицу:
.
В матрице 
преобразуем второй столбец в единичный. В качестве направляющего элемента выберем элемент 
. Так как направляющий элемент 
, то разделим вторую (направляющую) строку на 3:
.
Затем к первой строке прибавим вторую, умноженную на –3, и получим матрицу:
.
Третий столбец матрицы 
преобразуем в единичный. В качестве направляющего элемента выбираем элемент 
. Делим направляющую (третью) строку на 4:
.
Ко второй строке прибавляем третью, умноженную на –4/3, и получим матрицу:
.
Откуда
.
Проверкой убеждаемся, что .
▲
