Обозначим столбец неизвестных:
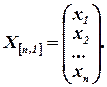
Обозначим столбец свободных членов:
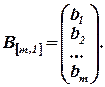
Тогда рассматриваемую систему линейных уравнений можно записать в виде одного матричного уравнения:
▼
Примеры
В рассмотренных ранее примерах системы линейных уравнений представляются в виде матричных уравнений:
1) 
эквивалентна
;
2) 
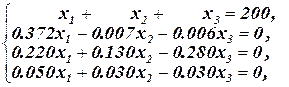
эквивалентна
;
3) 
эквивалентна
;
4) 
эквивалентна
.
▲
Систему линейных уравнений
можно представить расширенной матрицей
.
Определитель квадратной матрицы и его вычисление
Определитель есть число, определяемое для квадратной матрицы.
Системе линейных уравнений
из двух уравнений с двумя неизвестными соответствует квадратная матрица второго порядка
Исключая из системы поочередно каждое неизвестное, получим выражения:
Обозначим определитель второго порядка матрицы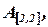 
вычисляемый по правилу:
Аналогично выводится правило для определителя третьего порядка:
Схематично обозначим в определителе произведения элементов, которые берутся со знаком плюс и минус:
Определителем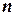 
–ого порядка, соответствующим матрице 
, называется определенная алгебраическая сумма 
всевозможных произведений 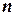элементов этой матрицы, взятых по одному в каждой строке и в каждом столбце.
Вычисление определителя для матрицы требует расчета произведений и определения знака их суммирования. При 
- это 
произведения, при 
- это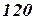 
произведений, а при 
- уже 
. Поэтому определители высоких порядков проще вычислять понижением порядка.
Минором 
-ого порядка элемента 
матрицы 
называется определитель 
матрицы, получающейся после вычеркивания из матрицы 
-ой строки и 
-ого столбца:
Алгебраическим дополнением элемента называется определитель:
.
Определитель 
равен сумме произведений всех элементов его -ой строки на их алгебраические дополнения:
Последнее выражение называется разложением определителя по -ой строке. Аналогичное разложение определителя можно получить и по любому его столбцу:
Вычисление определителя 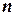-ого порядка понижением порядка сводится к вычислению 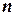определителей -ого порядка.
Специальным приемом можно снизить необходимое число рассчитываемых определителей, как это показано ниже на примере.
▼
Пример
Вычислить определитель матрицы
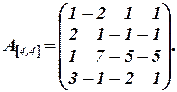
Решение.
А) Вычислим определитель способом понижения порядка, используя разложение по 
-ому столбцу:
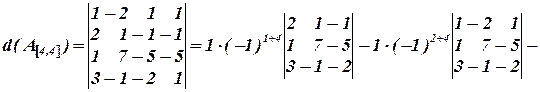
Ответ: 
Б) Вычислим определитель более рациональным способом, используя предварительные эквивалентные преобразования.
Следующее эквивалентное преобразование матрицы не влияет на величину ее определителя: прибавление к одной строке матрицы другой строки, умноженной на любое число.
Будем вычислять определитель путем разложения по 
-ой строке.
Преобразуем эту строку прибавлением к ней 
-ой строки с целью получения в ней больше нулевых элементов:
Продолжаем эквивалентные преобразования с той же целью, прибавляя к -ому столбцу утроенный -ой столбец:
Тогда
Ответ:
▲
