Нам нужно доказать измеримость объединения и пересечения счётного числа измеримых множеств. Пусть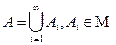 
. Покажем, что А 
M. Для этого представим сначала множество в виде суммы счётного числа попарно не пересекающихся множеств:
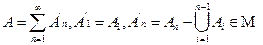
Так как
то
поэтому числовой знакоположительный ряд 
сходится и, следовательно, найдётся номер N такой, что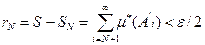 
. Далее, так как множество 
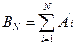измеримо, то найдётся множество B R(S) такое, что
А так как
,
то
,
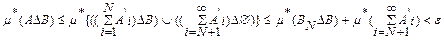что и означает измеримость множества А. Наконец, измеримость пересечения счётного числа измеримых множеств следует из измеримости дополнения измеримого множества и равенства
Теорема полностью доказана.
Замечания.
1) Совокупность M всех измеримых по Лебегу множеств A 
E имеет ту же мощность
гиперконтинуум, что и совокупность E0 всех частей E.
2) Существуют неизмеримые по Лебегу множества.
Мерой Лебега 
(A) называется внешняя мера *(A) на совокупности M всех измеримых по Лебегу множеств A E
Борелевские множества и борелевские функции
Классификация борелевских множеств на числовой прямой.
Борелевским множеством нулевого класса или борелевским множеством класса В0 на числовой прямой называется любое множество, открытое или замкнутое (относительно метрики 
(x, y) = |x – y|). Борелевским множеством первого класса или борелевским множеством класса В1 на числовой прямой называется любое множество, не являющееся ни открытым, ни замкнутым, но представимое в виде пересечения счётного числа открытых множеств или в виде объединения счётного числа замкнутых множеств. Борелевским множеством второго класса или борелевским множеством класса В2 на числовой прямой называется любое множество, не входящее ни в В0 , ни в В1 , но представимое в виде пересечения или объединения счётного множеств из В0 или из В1 . И т. д. с учётом всего набора ординальных чисел мощности 
. Заметим, что с учётом конструкции открытых и замкнутых множеств на числовой прямой с расстоянием
(x, y) = |x – y| вместо класса В0 можно было бы взять более узкий класс всех промежутков на числовой прямой. Заметим также, что совокупность всех борелевских множеств из промежутка [a, b) есть не что иное как минимальная 
- алгебра М(S) над полукольцом 
, то есть совокупность тех и только тех множеств из [a, b), которые получаются из множеств полукольца S с помощью операций не более чем счётных объединений или пересечений, выполняемых не более чем счётное число раз (с учётом всего набора ординальных чисел мощности ).
Классификация Бэра аналитически изобразимых на отрезке [a, b] функций.
Аналитически изобразимой функцией нулевого класса В'0 на отрезке [a, b] называется всякая непрерывная [a, b] на функция. Аналитически изобразимой функцией первого класса В'1 на отрезке [a, b] называется всякая функция, не являющаяся непрерывной на всём [a, b], но представимая на [a, b] как предел всюду на [a, b] сходящейся последовательности функций из класса В'0. Аналитически изобразимой функцией первого класса В'2 на отрезке [a, b] называется всякая функция, не входящая ни в В'0 , ни в В'1 , но представимая как предел всюду на [a, b] сходящейся последовательности функций из классов В'0 или В'1 . И т. д. с учётом всего набора ординальных чисел мощности . Заметим, что с учётом теоремы Вейерштрасса о том, что всякая непрерывная на отрезке [a, b] функция есть предел некоторой равномерно сходящейся на [a, b] последовательности полиномов, вместо класса В'0 можно было бы взять более узкий класс всех полиномов (или даже всех полиномов с рациональными коэфф-тами).
Замечание (о классификации аналитически изобразимых функций по Борелю).
Примеры: 1) функции с конечным числом точек разрыва, 2) функция Дирихле.
Литература: [ 2, гл. ХV; 12 ] из списка литературы 4-го семестра.
Задача 7. Покажите, что следуюшие функции являются аналитически изобразимыми
функциями первого класса:
а) функции со счётным числом точек разрыва,
б) монотонные функции и функции ограниченной вариации,
в) производные дифференцируемых всюду на [a, b] функций
