Совокупность M всех измеримых по Лебегу множеств A 
E является 
- алгеброй с единицей Е, а внешняя мера 
*(A) является - аддитивным продолжением
- аддитивная меры m с полукольца S на - алгебру M.
Доказательство.
Покажем, что M содержит S и * совпадает с на S.
Действительно, для всякого множества A 
S справедливо: * (A 
A) = *(
)= 0,
поэтому А измеримо. Далее, для всякого покрытия множества A S конечной или счётной системой множеств Ai S справедливо:
,
и равенство достигается, например, при А1 = А, А2 = А3 = … = .
Покажем, что * монотонна на M.
Действительно, если A M, В M, A В, то * (A) 
* (В), так как всякое покрытие множества В конечным или счётным набором множеств из полукольца S будет одновременно и покрытием множества А.
(3) Покажем, что * полуаддитивна на M, то есть
Действительно, так как
, где 
,
и при этом A’i Ai, A’i S и A’I 
A’j = при i 
j, то
Покажем, что M - алгебра с единицей Е.
Нам нужно показать, что объединение, пересечение и разность любых двух измеримых множеств А1 и А2 измеримо. Действительно, пусть А1 и А2 произвольные измеримые множества. Это означает, что
А так как
(проверьте это самостоятельно!), то
Но (В1 
В2) R(S), поэтому множество А1 А2 измеримо.
Измеримость дополнения всякого измеримого множества следует из равенства
Измеримость пересечения двух измеримых множеств следует из равенства
(5) Проверим, что для любых двух множеств А и В из Е выполняется:
Действительно, так как А В (А В) и В А (А В), то, в силу (3), имеем
Поэтому
(6) Покажем, что * аддитивна на M, то есть
С учётом индукции достаточно проверить справедливость этого утверждения при n = 2. Пусть множества А1 и А2 измеримы и А1 + А2 = А. Покажем, что
Так как множества А1 и А2 измеримы, то найдутся множества В1 и В2 из кольца R(S) такие, что
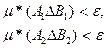
Так как множества А1 и А2 не пересекаются, то
(проверьте это самостоятельно!), и, следовательно,
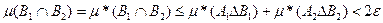
Далее, используя (5), получим
Так как мера аддитивна на R(S), то
Добавив к обеим частям этого равенства m (В1 В2), получим
откуда
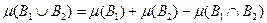
Воспользовавшись выше доказанными неравенствами, получим:
Заметим теперь, что
(проверьте это самостоятельно!). Поэтому
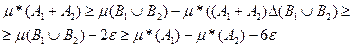
В силу возможности выбрать число 
> 0 произвольно малым заключаем, что
С другой стороны, так как объединение любых не более чем счётных покрытий множеств А1 и А2 является не более чем счётным покрытием множества А = А1 + А2, то
Поэтому
Итого получаем:
(7) Покажем, что * -аддитивна на M, то есть
Действительно, для любом натурального n справедливо:
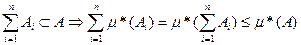
Переходя в этом неравенстве к пределу при n 
, получаем:
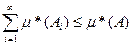
Доказательство противоположного неравенства проводится в полной аналогии с окончанием доказательства пункта (6) (проведите его самостоятельно!).
