Определённый интеграл Римана

 

Определения разбиения s:a = x₀ < x₁ < x₂ < …< x_n = b отрезка [a,b], диаметра разбиения d(s) = max Dx_i, где Dx_i = x_i – x_i-1 (i = 1, 2, …, n), интегральных сумм Римана

интеграла Римана

 

 

и интегрируемости по Риману f(x) Î R_[a,b].

Геометрическая и механическая интерпретации интеграла Римана.

Определение и геометрическая интерпретация нижней и верхней сумм Дарбу

и

где

, a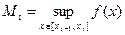

 

Из приведённых выше определений видно, что

 

Свойства сумм Дарбу:

1) При измельчении разбиения s (т. е. при добавлении новых точек разбиения) нижняя сумма Дарбу S (s) не убывает, а верхняя сумма Дарбу `S(s) не возрастает.

 

2) Всякая нижняя сумма Дарбу S (s₁) не превосходит всякой верхней суммы Дарбу ` S(s₂).

3) Существуют

Если функция интегрируема на отрезке, то она и ограничена на нём.

Если функция не ограничена на отрезке, то она и не интегрируема на нём.

 

 

Критерии интегрируемости по Риману

ограниченной на отрезке [a, b] функции f(x)

Критерий Дарбу

Ограниченная на отрезке функция интегрируема на нём по Риману тогда

и только тогда, когда разность её сумм Дарбу стремится к нулю

вместе с диаметром разбиения

Доказательство. “Þ” f(x) Î R_[a,b] , S(s, x) ® I,"e > 0 $d > 0 "s,

d(s) < d: | S(s, x) - I | < e/3. Переходя к точным нижним и верхним граням по всем x, получаем: "e > 0 $d > 0 "s, d(s) < d: | S (s) - I | £ e/3, | `S(s) – I | £ e/3, | `S(s) - S (s) | £ 2e/3 < e.

 

“Ü” ` S(s) - S (s)® 0, S (s) £ I £ `I £ `S(s), S (s) £ S(s, x)£`S(s),

поэтому S(s, x) ® I = I = `I #

 

Примеры: 1) непрерывные функции,

2) монотонные функции,

3) функция Дирихле.

Задача 2. Как связана интегрируемость функции

 

а) с условием sup_s inf_x S(s, x) = inf_s sup_x S(s, x),

 

б) с условием lim S(s_n, x) при n®¥ существует и одинаков для

любой последовательности разбиений s₁ Ì s₂ Ì s₃ Ì...

с d(s_n) ® 0 и при любом выборе x,

 

в) с условием lim S (s_n) = lim`S(s_n) для любой последовательности

разбиений s₁ Ì s₂ Ì s₃ Ì... с d(s_n) ® 0,

 

г) с условием lim [S(s’, x’) - S(s”, x”)] = 0

при max{d(s’), d(s”)} ® 0 и при любом выборе x’ и x”

д) с условием "e > 0 $s’, s”: `S(s”) - S (s’) < e

Задача 3. Проверьте выполнение условия Дарбу для функции Римана.

Критерий Римана

Ограниченная на отрезке функция интегрируема на нём по Риману тогда и только тогда, когда для любого a > 0 сумма длин тех сегментов разбиения, колебания функции на которых ³ a,

стремится к нулю вместе с диаметром разбиения

Доказательство. Проверим равносильность условий Дарбу и Римана.

 

“Þ” Пусть выполнено условие Дарбу. Тогда

“Ü” Пусть выполнено условие Римана. Тогда

 

 

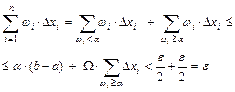
если сначала зафиксировать a < e/2(b-a), а затем взять d такое, что

 

где W = w(f, [a, b]) – колебание функции f(x) на сегменте [a, b].

 

 

Примеры: 1) непрерывные функции,

2) монотонные функции,

3) функция Дирихле.

Задача 4. Проверьте выполнение условия Римана для функции Римана.

Лемма Бэра (о связи между колебаниями функции на сегменте

и в точках этого сегмента относительно сегмента)

 

1) колебание функции в любой точке сегмента (относительно этого сегмента) не больше колебания функции на всём сегменте; колебание функции на сегменте не меньше колебания в любой точке сегмента (относительно этого сегмента),

 

2) если в каждой точке сегмента D колебание функции < a,

то $ d > 0 такое, что на " сегменте D¢Ì D длиной < d

колебание функции будет < a.

 

Доказательство. 1) следует непосредственно из определений колебания функции на множестве и в точке. 2) докажем от противного. Пусть в каждой точке x сегмента [a, b] колебание функции w(f, x) будет < a, но "d > 0 $ сегмент [a¢, b’]Ì [a, b] длиной b' - a' < d, колебание функции на котором w(f, [a’, b’]) будет ³ a. Тогда существует последовательность сегментов [a_n, b_n] из [a, b] таких, что b_n - a_n ® 0, но w(f, [a_n, b_n]) ³ a. Из ограниченной последовательности a_n, a £ a_n £ b можно выбрать подпоследовательность a_Кn , a £ a_Кn £ b,сходящуюся к некоторому числу x, a £ x £ b, при этом b_Кn - a_Кn ® 0. Но любая окрестность этой точки x (в пересечении с сегментом [a, b]) содержит некоторый сегмент [a_Кn , b_Кn], колебание функции на котором w(f, [a_Кn , b_Кn]) будет ³ a. Поэтому и w(f, x) будет ³ a (?!).

Критерий дю Буа-Реймона

Обозначим Е_a = { x Î [a, b] таких, что w(f, x) ³ a }

 

 

Ограниченная на отрезке функция интегрируема на нём по Риману тогда и только тогда, когда для любого a > 0 множество E_a всех тех точек разрыва функции f(x), колебание в которых ³ a, имеет жорданову меру нуль, то есть оно может быть заключено в конечную систему интервалов общей сколь угодно малой длины

Доказательство. Проверим равносильность условий Римана и дю Буа-Реймона.

 

“Þ” Пусть выполнено условие Римана. Тогда

“Ü” Пусть выполнено условие дю Буа-Реймона. Тогда pg(E_a) = 0, то есть

Не умаляя общности, можно считать, что эти интервалы попарно не пересекаются и попарно не соприкасаются (всякие два пересекающихся или соприкасающихся друг с другом интервала (a’, b’) и (a”, b”) можно без увеличения суммарной длины заменить одним интервалом (min{a’,a”}, max{b’, b”})). Обозначим через D₁ , D₂ ,… сегменты-промежутки между соседними интервалами; число таких сегментов будет не больше к+1, и в каждой точке любого их этих сегментов колебание функции w(f, x) будет < a. Выберем теперь, в соответствии с утверждением 2) леммы Бэра, для каждого из сегментов D_j своё d_j и обозначим за d’ наименьшее из всех d_j (j=1, 2, 3, …, k+1). Тогда для любого разбиения s с диаметром d(s) < d’ всякий сегмент [x_i-1, x_i] этого разбиения, колебание w(f, [x_i-1, x_i]) на котором будет ³ a, не лежит целиком ни в одном из сегментов D_j . Поэтому для суммарной длины таких сегментов справедлива оценка:

при d(s) < d, если сначала зафиксировать конечный набор (a_i, b_i) с суммой длин меньше e/2, а затем взять d = min{d’, e/4k}. #

Примеры: 1) непрерывные функции,

2) монотонные функции,

3) функция Дирихле.

Задача 5. Проверьте выполнение условия дю Буа-Реймона для ф-ии Римана.

 

Критерий Лебега

Обозначим Е = { x Î [a, b] таких, что w(f, x) > 0 }

 

Ограниченная на отрезке функция интегрируема на нём по Риману тогда и только тогда, когда множество всех её точек разрыва имеет лебегову меру нуль, то есть оно может быть заключено в конечную или счётную систему интервалов общей сколь угодно малой длины

Доказательство. Проверим равносильность условий дю Буа-Реймона и Лебега.

 

“Þ” Пусть выполнено условие дю Буа-Реймона, то есть для любого a > 0 множество E_a всех тех точек разрыва функции f(x), колебание в которых ³ a, может быть заключено в конечную систему интервалов общей сколь угодно малой длины. Заметим, что

Для каждого n покроем множество E_1/n конечным набором интервалов общей длины меньше e/2ⁿ. Тогда объединение по всем n ÎN таких наборов будет не более чем счётным набором интервалов, вместе (в объединении) покрывающих множество E и имеющих суммарную длину меньше e/2 + e/4 +e/8 +...= e.

 

“Ü” Пусть выполнено условие Лебега. Тогда множество E всех точек разрыва функции f(x), а вместе с ним и множество Е_a Ì Е для любого a > 0 может быть заключено в конечную или счётную систему интервалов общей сколь угодно малой длины. Осталось заметить, что множество Е_a для любого a > 0 компактно, то есть (в соответствии с критерием компактности на числовой прямой с обычным расстоянием) замкнуто и ограничено. Ограниченность множества Е_a очевидна, Е_a Ì [a, b]. Проверим замкнутость Е_a . Согласно критерию замкнутости, нужно показать, что (Е_a)’ Ì Е_a. Пусть x Î (Е_a)’. Тогда во множестве Е_a найдётся последовательность x_n такая, что x_n ® x. Так как в любой окрестности Ux точки x содержатся все x_n, начиная с некоторого номера, то w(f,Ux) будет ³ w(f, x_n) ³ a. Поэтому и w(f, x) = inf w(f,Ux) будет ³ a, то есть x Î Е_a. #

 

Примеры: 1) непрерывные функции,

2) монотонные функции,

3) функция Дирихле.

 

 

Замечания (о множествах меры нуль):

1) всякое конечное множество есть множество жордановой меры нуль, а всякое

конечное или счётное множество есть множество лебеговой меры нуль,

2) всякое множество жордановой меры нуль есть и множество лебеговой меры

нуль. Обратное, вообще говоря, не верно. Например, множество [a, b] Ç Q

есть множество лебеговой меры нуль, но не жордановой меры нуль,

3) всякое компактное множество лебеговой меры нуль есть и множество

жордановой меры нуль,

4) объединение любого конечного числа множеств жордановой меры нуль есть

множество жордановой меры нуль, а объединение любого конечного или

счётного числа множеств лебеговой меры нуль есть множество лебеговой

меры нуль.

 

 

Задача 6. Проверьте выполнение условия Лебега для функции Римана.

Задача 7. Покажите, что интегрируемость по Риману и значение

интеграла Римана не изменятся при изменении значений

функции в любом конечном числе точек, но могут

измениться при изменении значений функции

в счётном числе точек.

14. Функциональные ряды

 

Функциональным рядом называется выражение вида

 

a(x): а₁(x) + а₂(x) + …+ а_n(x) + …,

то есть числовые ряд, зависящий от параметр х. В частности, функциональными рядами будут степенные ряды

 

a(x): а₀ + а₁ (x – x₀) + …+ а_n (x – x₀)ⁿ + …

 

и тригонометрические ряды

a(x): а₀ /2 + (а₁ sin x + b₁ cos x) + …+ (a_n sin nx + b_n cos nx) + …

 

Областью сходимости функционального ряда а(x) называется множество всех тех значений параметра x, при которых слагаемые ряда а_n(x) определены, а сам ряд а(x) сходится.

При построении теории функциональных рядов возникают, в частности, следующие вопросы:

 

1) Что можно сказать о свойствах суммы S(x) функционального ряда а(x),

зная свойства его слагаемых а_n(x) или свойства его частичных сумм S_n(x)?

Переносятся ли, например, свойства конечных сумм S_n(x) на бесконечные

(счётные) суммы S(x)?

 

2) Можно ли данную функцию представить рядом данного вида (то есть как по данной функции определить коэффициенты ряда данного вида, суммой которого в указанной области данная функция является, и как проверить сходимость полученного ряда именно к данной функции во всей указанной области)?

 

3) Можно ли данный ряд дифференцировать или интегрировать почленно? И т. п.

 

Так уже в начале XIX века было установлено, что сумма S(x) степенного ряда с всюду непрерывными слагаемыми a_n(x) = a_n (x - x₀)ⁿ и с всюду непрерывными частичными суммами S_n(x) сама является непрерывной функцией на всём промежутке сходимости степенного ряда. Однако для произвольных рядов это оказалось неверным: в 1826 г. Абель показал, что сумма S(x) тригонометрического ряда Бернулли

 

sin x – (sin 2x)/2 + (sin 3x)/3 + …+ (-1)ⁿ⁺¹(sin nx)/n + …

 

разрывна в точках x = (2k + 1) , где k Z. В связи с этим встал вопрос об условиях непрерывности суммы ряда непрерывных слагаемых. Остановимся на этом вопросе подробнее.

Пусть ряд a(x) со слагаемыми a_n(x), непрерывными на множестве A (относительно A), сходится при каждом фиксированном x A к S(x), то есть

 

 

Условие непрерывности S(x) на множестве A (относительно A) запишется в виде

 

 

Но

| S(x) – S(x₀)| | S(x) – S_n(x)| + | S_n(x) – S_n(x₀)| + | S_n(x₀) – S(x₀)|

 

Так как S_n(x₀) S(x₀), то при достаточно больших n третье слагаемое будет < . Второе слагаемое для любого фиксированного n также можно сделать < за счёт непрерывности S_n(x) в точке x₀:

Всё дело, таким образом, в оценке первого слагаемого | (x)| = |S(x) - S_n(x)|. Но оно с гарантией не превосходит = sup| (x)| (точная верхняя грань берётся по всем x A). Поэтому, если ® 0 при , то и первое слагаемое будет < при достаточно больших n. Условие

 

при (_*)

достаточное для непрерывности суммы ряда непрерывных слагаемых, было названо Вейерштрассом (1841 г.) равномерной сходимостью (глобальной равномерной сходимостью, или ещё А₁ - сходимостью) ряда a(x) на множестве А. Таким образом,

 

A₁ – cходимость:

Условие A₁ – cходимости значительно сильнее условия простой (или поточечной) сходимости ряда a(x) при каждом фиксированном x A (+ графическая интерпретация равномерной и простой сходимостей последовательности S_n(x) к S_n(x) на промежутке).

+ примеры: 1) ,

 

2) ,

 

3)

 

Для равномерной A₁ – cх-ти ряда a(x) на множестве A справедлив критерий Коши:

 

ряд a(x) равномерно A₁ – сходится на множестве A Û

(_**)

 

Действительно, если ряд a(x) равномерно A₁ – сходится на множестве A, то

и

Поэтому

Наоборот, если выполнено условие (_**), то заменяя в нём на и переходя к пределу при фиксированном n и m = n + p , получаем

,

 

что и означает равномерную A₁ – сходимость ряда a(x) на множестве A.

 

Далее, Вейерштрасс показал, что для равномерной сходимости ряда a(x) на множестве A достаточно, чтобы

ряд a(x) сходился правильно, то есть был бы мажорируем на множестве A некоторым сходящимся числовым рядом: существует сходящийся числовой ряд такой, что при каждом x A и при каждом n N

Доказательство этого утверждения следует из неравенства

 

 

с учётом критерия Коши.

 

 

Задача 13. Покажите, что всякий равномерно сходящийся ряд становится

правильно сходящимся при подходящей группировке его слагаемых

(слагаемые ряда предполагаются ограниченными).

 

 

Теорема (критерий Дини непрерывности суммы ряда непрерывных слагаемых).

Пусть ряд a(x) со слагаемыми a_n(x), непрерывными на множестве A (относительно A), сходится просто (поточечно) при каждом фиксированном x A к S(x). Тогда для того, чтобы сумма ряда S(x) была непрерывна на множестве А, необходимо и достаточно, чтобы ряд a(x) В₃ -сходился (обобщённо поточечно равномерно сходился) к S(x) на множестве А, то есть чтобы выполнялось условие B₃ – cходимости:

 

 

Доказательство.

«» Пусть ряд a(x) просто и В₃ –сходится к S(x) на множестве А. Покажем, что сумма ряда S(x) непрерывна на множестве А. Зафиксируем произвольные x₀ A и > 0 и подберём > 0 так, чтобы при |x – x₀| < выполнялось | S(x) – S(x₀)| < . Так как S_n(x₀) S(x₀) при n , то

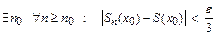
А так как ряд a(x) В₃ -сходится к S(x) на множестве А, то

 

Далее, в силу непрерывности S_n(x) в точке x₀

 

 

Тогда при |x – x₀| < = min{ , } получаем, что

 

| S(x) – S(x₀)| £ | S(x) – S_n(x)| + | S_n(x) – S_n(x₀)| + | S_n(x₀) – S(x₀)| <

«» Пусть сумма ряда S(x) непрерывна на множестве А, а ряд a(x) просто сходится к S(x) на множестве А. Покажем, что тогда ряд a(x) В₃ –сходится к S(x) на множестве А. Заметим, что n разность _n(x) = S(x) - S_n(x) также будет непрерывна на множестве А. Поэтому

 

 

Пусть n₀ - любой фиксированный номер. Так как _n (x₀) 0 при n , то

 

 

При таком номере n и при соответствующем этому номеру > 0 будем иметь:

 

,

 

что и означает, что ряд a(x) В₃ –сходится к S(x) на множестве А. #

 

Замечания.

 

1) Из доказанного выше критерия Дини следует, что если ряд a(x) со слагаемыми a_n(x), непрерывными на множестве A (относительно A), сходится просто (поточечно) при каждом фиксированном x Î A к S(x), то для того, чтобы сумма ряда S(x) была непрерывна в данной точке x₀ множества А (относительно A),

необходимо и достаточно, чтобы выполнялось условие

 

 

2) Подробнее о разных видах равномерной сходимости см., например,

“История математики. Анализ. Часть II.”

//Методические указания, изд-во ИГУ, 1996, стр. 7-12.

+ пример:

Задача 14. Обозначим N(x, ) = { n таких, что | S_n(x) – S(x)| < }. Покажите:

 

1) простая сходимость ряда a(x) к S(x) на множестве А означает,

что множество N(x, ) содержит все номера,

начиная с некоторого номера n₀ ,

 

2) равномерная А₁ -сходимость ряда a(x) к S(x) на множестве А означает,

что пересечение множеств N(x, ) по всем x A

содержит все номера, начиная с некоторого номера n₀ ,

 

3) В₃ - сходимость ряда a(x) к S(x) на компакте А означает, что

существует разбиение множества N всех номеров на «отрезки» [1, n₁],

[n₁ + 1, n₂], … такое, что множество N(x, ) содержит номера из всех отрезков.

 

Теорема Дини. Если ряд a(x) с непрерывными слагаемыми одного знака сходится

на компакте А к непрерывной S(x) просто, то тогда ряд a(x)

сходится к S(x) и равномерно на А.

Доказательство. С учётом критерия Дини, нужно показать, что в случае, когда множество А – компакт, а слагаемые ряда а(x) одного знака (например, а_n(x) 0), В₃ – сходимость становится равносильной А₁ – сходимости. Действительно, так как величины |S_n(x) – S(x)| образуют монотонную при любом фиксированном n последовательность, и выполнено условие В₃ – сходимости, то

 

 

При этом соответствующие – окрестности |x – x₀| < , x₀ A, = (, x₀) образуют открытое покрытие множества А. В силу компактности А, из этого покрытия можно выделить конечное подпокрытие .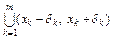

Тогда при n n₀ = max {n₁, n₂, …, n_m} (где n_k соответствует x_k) справедливо: |S_n(x) – S(x)| < e, что и означает равномерную А₁ – сходимость ряда a(x) к S(x).

 

 

Замечания.

1) Равномерную А₁ – сходимость последовательности функций S_n(x) к функции S(x)

часто обозначают так: S_n(x) S(x)

2) Теорема Дини указывает критерий равномерной сходимости ряда а(x)

(последовательности S_n(x)) к S(x) в случае, когда слагаемые ряда а(x)

непрерывны и одного знака (последовательность непрерыных функций S_n(x)

монотонно сходится к S(x)), а множество А – компакт:

 

S_n(x) S(x) на А S(x) непрерывна на А

 

Некоторые обобщённые методы суммирования рядов

 

Рассмотрим следующие ряды

а: 1 – 1 + 1 – 1 + …+ (-1)ⁿ⁺¹ + …

b: sin1 + sin2 + … + sin n + …

c: 1 + 2 + 4 + 8 + 16 + …+ 2^n-1 + …

Все эти ряды расходятся в обычном смысле (так как их слагаемые не стремятся к нулю при n ). Попытаемся так обобщить понятие сходимости ряда и суммы ряда, чтобы:

 

1) некоторые расходящиеся в обычном смысле ряды стали бы сходящимися в том или ином обобщённом смысле (содержательность);

 

2) все ряды, сходящиеся в обычном смысле,

сходились бы и в смысле обобщённой сходимости (регулярность);

 

3) сходящиеся в смысле обобщённой сходимости ряды образовывали бы линейное пространство (линейность).

 

Такие обобщения понятия сходимости и суммы ряда возможны, например:

 

ряд a: а₁ + а₂ + …+ а_n + … называется сходящимся по Фробениусу – Чезаро, если сходится послед-ть S_n^ср. = (S₁ + S₂ + … + S_n)/n средних частичных сумм ряда a; при этом S^ср = lim S_n^ср называется суммой Фробениуса – Чезаро ряда a

числовой ряд a: а₀ + а₁ + а₂ + …+ а_n + … называется сходящимся по Абелю –Пуассону, если радиус сходимости степенного ряда a(х): а₀ + а₁ х + а₂ х² + …+ а_n хⁿ + …

не меньше 1; при этом величина S = lim S_n(х) при х 1 - 0 называется суммой Абеля - Пуассона ряда a

 

степенной ряд a(x): а₀ + а₁ (x – x₀) + а₂ (x – x₀)² + …+ а_n (x – x₀)ⁿ + … называется сходящимся по Эйлеру в данной точке х, если существует функция S(х), для которой данный степенной ряд является её рядом Тейлора в точке х₀, то есть выполнено условие (_**); при этом величина S(х) называется суммой Эйлера ряда a в точке х

 

+ проверка линейности, регулярности и содержательности (на примере ряда а)

всех трёх указанных обобщений понятия сходимости и суммы ряда

 

 

Задача 17. а) Исследуйте ряд b на сходимость по Фробениусу – Чезаро.

б) Исследуйте ряд с на сходимость по Фробениусу – Чезаро,

на сходимость по Абелю – Пуассону и на сходимость по Эйлеру.

Мера и интеграл Лебега

Системы множеств

 

Система множеств S называется полукольцом, если

1) S,

2) если A S и B S, то и A B S,

3) если A S, A₁ S и A₁ A, то множество A представимо в виде

A = A₁ + A₂ + A₃ + … + A_k , где все A_i принадлежат S.

 

Множество Е S называется единицей системы множеств S, если

A S: A E A

Единицей Е системы множеств S может быть только объединение всех множеств, входящих в S. Таким образом, система множеств S будет системой множеств с единицей тогда и только тогда, когда объединение всех множеств, входящих в S, есть множество принадлежащее S.

 

Система множеств R называется кольцом, если вместе с каждыми двумя множествами она содержит и их пересечение, объединение и разность, то есть

если A R и B R, то и A B R, A B R, A - B R.

 

Всякое кольцо является и полукольцом, так как = A - A R, и если A R, A₁ R и A₁ A, то множество A представимо в виде A = A₁ + A₂ , где A₂ = A – A₁ R.

 

Всякое кольцо R вместе с каждыми двумя множествами А и В содержит также и их симметрическую разность A D B = (A - B) + (В - А). Всякое кольцо есть, таким образом, система множеств, замкнутая относительно операций пересечения, объединения, разности и симметрической разности, выполняемых любое конечное число раз.

 

Кольцо R с единицей называется алгеброй множеств и обозначается M.

 

Кольцо R называется кольцом, порождённым системой множеств S и обозначается R(S), если оно является наименьшим из всех колец, содержащих систему множеств S. Кольцо R(S), порождённое системой множеств S, есть пересечение всех колец, содержащих S. Кольцо R(S), порождённое полукольцом S, есть совокупность тех и только тех множеств, которые представимы в виде суммы конечного числа попарно не пересекающихся множеств из полукольца S, то есть если кольцо R порождено полукольцом S, то

 

A R(S) A = A₁ + A₂ + … + A_k, где все A_i S

 

Кольцо R называется - кольцом, если оно замкнуто относительно объединения любого счётного числа множеств, то есть если все A_i (i = 1, 2, 3, …) принадлежат R, то и их объединение также принадлежит R.

 

- кольцо R с единицей называется - алгеброй множеств. Другими словами,

- алгеброй множеств называется алгебра множеств M, замкнутая относительно объединения любого счётного числа множеств. Если M - - алгебра множеств, то она замкнута и относительно пересечения любого счётного числа множеств, так как

 

- кольцо R называется - кольцом, порождённым системой множеств S и обозначается R(S), если оно является наименьшим из всех s - колец, содержащих систему множеств S. - кольцо R(S), порождённое системой множеств S, есть пересечение всех - колец, содержащих S. - кольцо R(S), порождённое полукольцом S, есть совокупность тех и только тех множеств, которые представимы в виде суммы конечного или счётного числа множеств из полукольца S, то есть

если - кольцо R(S) порождено полукольцом S, то

 

A R(S) A = A₁ + A₂ + … + A_k + …, где все A_i S

 

+ примеры:

 

1) - не полукольцо,

2) - полукольцо с единицей,

3) - полукольцо c единицей,

4) - полукольцо с единицей,

5) - полукольцо без единицы,

1') - не полукольцо,

2') - полукольцо с единицей,

3') - полукольцо c единицей,

4') - полукольцо с единицей,

5') - полукольцо без единицы,

 

6) S – совокупность всех конечных подмножеств данного множества,

 

7) S - полная система попарно несовместных элементарных событий,

S = { , A₁, A₂, …, A_n, }

Лебегово продолжение меры

 

Заметим сначала, что попытка продолжения меры Пеано-Жордана pg с кольца R(S) на возможно более широкую - алгебру (или - кольцо) множеств наталкивается на следующие проблемы:

1) мера pg аддитивна на полукольце S и, следовательно, на кольце R(S),

но она не аддитивна даже на минимальной - алгебре M(S)

борелевских множеств, так как, например:

2) минимальная - алгебра борелевских множеств M(S) имеет мощность

континуум, в то время как максимальная - алгебра множеств

M° = {A E} = E° имеет мощность гиперконтинуум,

 

 

Пусть – - аддитивная мера на полукольце с единицей Е. Продолжим её

с полукольца S на кольцо R(S) и для всякого множества A E определим его внешнюю меру *(A) как где точная нижняя грань берётся по всем возможным покрытиям множества A E конечными или счётными системами множеств A_i S.

 

 

Будем говорить, что множество A E измеримо (измеримо по Лебегу), если

 

 

+ пример: