Лабораторная работа №2: «Решение нелинейных уравнений методом хорд и касательных».

Лабораторная работа №1: «Решение нелинейных уравнений методом половинного деления».

Задание:

1) Отделить корни аналитически и уточнить один из них методом половинного деления с точностью до 0,01.

2) Отделить корни графически и уточнить один из них методом половинного деления с точностью до 0,01.

Вар.№1: Вар.№2:

 

 

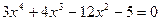
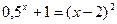
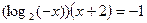
Вар.№3: Вар.№4:

 

 

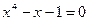
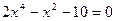
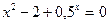
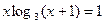
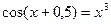
Вар.№5: Вар.№6: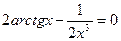

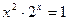
Образец выполнения задания:

1) Отделить корни аналитически.

.Обозначим, Находим корень производной:

Составим таблицу знаков функции f(x), полагая х равным: 1) критическим значениям функции (корням производной) или близким к ним; 2) граничным значениям (исходя из области определения функции):

X	-¥		+¥
Sign f(x)	+	-	+

 

Так как происходят две перемены знака функции, то уравнение имеет два действительных корня. Чтобы завершить операцию отделения корней, следует уменьшить промежутки, содержащие корни, так, чтобы их длина была не больше 1. Для этого составим новую таблицу функции f(x):

x	-1
Sign f(x)	+	-	-	+

Отсюда видно, что корни заключены в следующих промежутках:

х₁Î[-1;0],x₂Î[1;2].

 

2) Отделить корни аналитически и уточнить один из них методом половинного деления с точностью до 0,001.

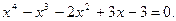
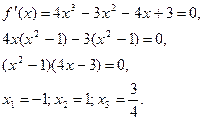
Составим таблицу знаков функции f(x):

X	-¥	-1	3/4		+¥
Sign(x)	+	-	-	-	+

Из таблицы видно, что уравнение имеет два действительных корня:

х₁Î(-¥;-1];x₂Î[1;+¥).

Уменьшим промежутки, в которых находятся корни:

x	-2	-1
Sign f(x)	+	-	-	+

Следовательно, х₁Î[-2;-1]; х₂Î[1;2]. Уточним один из корней, например х₁Î[-2;-1], методом половинного деления до сотых долей. Все вычисления удобно производить, используя следующую таблицу:

n	an(+)	bn(-)	xn=	f(xn)
	-2	-1	-1,5	-3,5625
	-2	-1,5	-1,75	0,3633
	-1,75	-1,5	-1,63	-1,8140
	-1,75	-1,63	-1,69	-0,7981
	-1,75	-1,69	-1,72	-0,2363
	-1,75	-1,72	-1,73	-0,0406
	-1,75	-1,73	-1,74	0,1592
	-1,74	-1,73

Ответ: х1»-1,73.

3) Отделить корни графически и уточнить один из них методом половинного деления с точностью до 0,01.

.

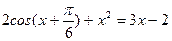Перепишем уравнение в виде: 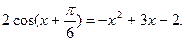Обозначим

построим графики этих функций и увидим, что уравнение имеет два корня: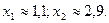

Уточним первый из них методом половинного деления:

 

n	an(+)	bn(-)	xn=	f(xn)
		1,5	1,25	-0,59033
		1,25	1,125	-0,264823
		1,125	1,0625	-0,089197
		1,0625	1,03125	0,00162
	1,03125	1,0625	1,046875	-0,044033
	1,03125	1,046875	1,039063	-0,021267
	1,03125	1,039063	1,035156	-0,009838
	1,03125	1,035156	1,033203	-0,004113
	1,03125	1,033203	1,032227	-0,001247
	1,03125	1,032227	1,031738	0,000186
	1,031738	1,032227	1,031982	-0,00053
	1,031738	1,031982	1,03186	-0,000172
	1,031738	1,03186	1,031799	7,1E-06

Ответ: х1»1,03.

Лабораторная работа №2: «Решение нелинейных уравнений методом хорд и касательных».

1. Метод хорд.

Образец выполнения задания.

1.Отделить корни графически уточнить один из них методом хорд до 0,001.

tg(0,55x+0,1)=x²

Обозначим у₁= tg(0,55x+0,1) у₂=x²

Составим таблицу значений:

X		0,2	0,4	0,6	0,8
Y2=X2		0,04	0,16	0,36	0,64
0,55x+0,1	0,1	0,21	0,32	0,43	0,54	0,65
Y1	0,100335	0,213142	0,331389	0,458621	0,59943	0,760204

Построим график:

Видим, что хÎ[0,6;0,8].

Чтобы уточнить его методом хорд, определим знаки функции на концах отрезка

[0,6;0,8] и знак её второй производной в этом промежутке:

f (0,6)=tg0,43-0,36=0,0986

f (0,8)=tg0,54-0,64=-0,0406

f’ (x)=0,55/(cos²(0,55x+0,1))-2x

f’’ (x)=0,55×2cos^-3(0,55x+0,1)×sin(0,55x+0,1)×0,55-2<0 при хÎ[0,6;0,8].

f’’ (x)× f (0,8)>0, значит х₀=0,6

Для вычислений используем формулу:

, где b=0,8, x₀=0,6.

Вычисления производим в таблице:

n	xn
	0,60000	-0,14168
	0,74168	-0,0081
	0,74978	-0,00039
	0,75017	-1,9E-05
	0,75019	-8,9E-07

Ответ: х»0,750.

 

2. Отделить корни аналитически и уточнить один из них методом хорд до 0,001.

f (x)=x³-0,2x²+0,5x+1,5

f’ (x)=3x²-0,4x+0,5 D=0,16-6<0

Составим таблицу знаков f (x):

x	-	-1		+
Sign f(x)	-	-	+	+

 

Получаем один действительный корень в промежутке [-1; 0].

Чтобы уточнить его, найдём 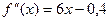, в промежутке [-1; 0] ,

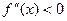f’’ (a)× f (х)>0, значит х₀=b=0.

Вычисления произведём по формуле:

,

где a=-1, х₀=b=0, f (a)= f (-1)-1-0,2-0,5+1,5=-0,2.

Вычисления производим в виде таблицы:

n	xn	xn3	xn2	0,2xn2	0,5xn	f(xn)	f(xn)+0,2	xn-a	h
						1,5	1,7		-0,11765
	-0,88235	-0,68695	0,77855	0,15571	-0,44118	0,21616	0,41616	0,11765	-0,05654
	-0,94346	-0,83979	0,89012	0,17802	-0,47173	0,01045	0,21045	0,05654	-0,05373
	-0,94627	-0,84731	0,89543	0,17909	-0,47313	0,00047	0,20047	0,05373	-0,05361
	-0,94639

Ответ: х»-0,946

 

1. Метод касательных (Ньютона).

, где x₀=a, если f(a)×f’’(x)>0; x0=b, если f(b)×f’’(x)>0 на [a;b].

1-е задание: tg(0,55x+0,1)=x² , где хÎ[0,6;0,8] (см. решение выше).

Так как f(0,6)>0,f(0,8)<0, f’’(x)<0, то за начальное приближение берём х₀=0,8. Вычисления производим по формуле:

f’(0,8)=0,55/(cos²(0,55x+0,1))-2x=-0,8523.

Вычисления производим в виде таблицы:

n	xn		f’ (x)=0,55/(cos2(0,55x+0,1))-2x
	0,8	-0,04057	-0,85238	0,047597
	0,752403	-0,001724	-0,77961	0,002211
	0,750192	0,00000	-0,77619	0,00000

Ответ: х»0,750

 

2-е задание: f (x)=x³-0,2x²+0,5x+1,5 f’(x)=3x²-0,4x+0,5

Так как f(0)>0,f(-1)<0, f’’(x)<0, то за начальное приближение берём х₀=-1.

n	xn	f (x)=x3-0,2x2+0,5x+1,5	f’(x)=3x2-0,4x+0,5
	-1	-0,2	3,9	-0,05128
	-0,94872	-0,008281	3,579684	-0,00231
	-0,9464	-0,00000	3,565608	-0,00000

Ответ: х»-0,946

Самостоятельно: 1) x-sinx=0,25; x³-3x²+9x-8=0

2) tg(0,58x+0,1)=x² ; x³-6x²-8x=0

3) tg(0,4x+0,4)=x²; x³-0,1x²+0,4x-1,5=0

4) lnx-7/(2x+6)=0; x³-3x²+9x+2=0

5) tg(0,5x+0,2)=x² ; x³+0,2x²+0,5x-1,2=0

Лабораторная работа №4: