Падение и потеря напряжения в 3-х фазной ЛЭП или трансформаторе с симметричной нагрузкой

На схеме замещения одной фазы электропередачи, приведенной на рис. 4.1:

r – активное сопротивление провода ЛЭП.

х – реактивное сопротивление провода.

Zнагр – комплексное сопротивление нагрузки (характеризуется углом φ).

Рис. 4.1. Схема замещения одной фазы электропередачи.

Считаем - известно. Построим векторную диаграмму и найдем вектор (рис. 4.2).

Рис. 4.2. Векторная диаграмма электропередачи.

ас – падение напряжения.

аb – потеря напряжения.

На практике отрезок ad считают потерей напряжения, пренебрегая отрезком db.

- продольная слагающая падения напряжения (потеря).

,

.

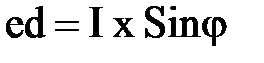- фазная потеря напряжения.

- линейная потеря. Умножим и разделим на Uн: .

Примеры решения задач

3.2.1. Два потребителя получают питание по трехфазной четырехпровод-ной воздушной ЛЭП U_н =380, выполненной алюминиевыми проводами одного сечения (см рис.). Выбрать сечение проводов из условия допусти­мой потери напряжения ΔU_доп = 5% (ΔU_доп = 380 ∙ 0,05=19 В).

Рис.4. Схема электропередачи.

Реактивные мощности потребителей:

Q₁=P₁∙tgφ₁=40∙0,48=19,2 кВАр, Q₂=P₂∙tgφ₂=30∙0,75=22,5 кВАр.

Погонное реактивное сопротивление x₀ зависит от сечения проводов, кото­рое неизвестно. Поэтому принимаем его на уровне максимального значения для воздушных ЛЭП напряжением ниже 1000 В: x₀= 0,35 Ом/км(табл.П.1.2). Тогда реактив­ная слагающая потери напряжения на участке А – В,:

Допустимая активная слагающая потери напряжения: ΔU_Адоп = 19-8=11 В.

Сечение провода:

Где для алюминиевых проводов γ = 0,032 км/Ом∙мм², ρ=31,25 Ом∙мм²/км.

Подходящие стандартные сечения: 95 и 120 мм².

Расчет фактической потери напряжения для F = 95 мм². По табл. П1.1, П1.2: r₀=0,315 Ом/км, x₀=0,29 Ом/км.

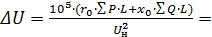
Сечение F = 95 мм² проходит по допустимой потере напряжения.

Расчет фактической потери напряжения для F = 70 мм². По табл. П1.1, П1.2: r₀=0,425 Ом/км, x₀=0,3 Ом/км.

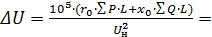
Сечение F = 70 мм² не проходит по допустимой потере напряжения.

Проверка выбранного сечения 95 мм² по нагреву: по табл. П1.1 для голого алюминиевого провода F = 95 мм² - I_дд = 320 А.

Расчетный ток наиболее нагруженного участка участка А-Б:

320 А > 124 А, провод F = 95 мм² проходит по нагреву (j_дд=3,3 А/мм²).

Плотность тока на участке А-Б: j_А-Б=124/95=1,3 А\мм² близка к экономи­ческой (табл. П1.6).

 

3.2.2. Определить размах отклонений напряжения на вторичной стороне трансформатора типа ТМЗ-630/10, если на стороне НН трансформатора мак­симальная нагрузка составляет Рм=520 кВт, cosφ =0,8 а минимальная на­грузка – Р’=130 кВт, cosφ =0,8. Размах отклонений напряжения выразить в процентах от номинального напряжения обмотки ВН трансформатора.

Решение.

По табл. П1.8 параметры трансформатора ТМЗ 630 - 10 / 0,4: Uк = 5,5%, ∆Рк = 7,6 кВт = 7600 Bт, Iхх= 1,8 %, ∆Рхх = 1,68 кВт.

Сопротивления трансформатора, приведенные к стороне ВН

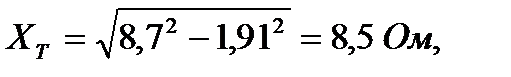
Максимальная реактивная нагрузка Qм = Рм ∙Sinφ =520 ∙ 0,6 = 312 кВАр.

Потеря напряжения в максимальном режиме

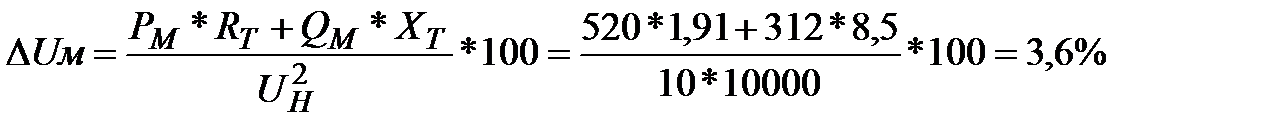
Потеря напряжения в минимальном режиме

Размах отклонений напряжения ΔV = 3,6 – 0,9 = 2.7%.

 

3.2.3 Определить потери напряжения (%) в трансформаторе типа ТМН-4000/35 при двух значениях коэффициента мощности 0,6 и 0,95, если на­грузка трансформатора равна 3,5 МВ·А.

Решение.

По справочнику трансформатор ТМН4000 - 35 / 6,3: Uк = 7,5%, ∆Рк = 33 кВт = 33000 Bт, Iхх= 0,9 %, ∆Рхх = 5 кВт.

Сопротивления трансформатора, приведенные к стороне ВН

Cos φ= 0,6, Sinφ= 0,8, P = 3,5 ∙ 0,6 =2,1 МВт, Q = 3,5 ∙ 0,8 =2,8 МВАр.

 

Cos φ= 0,95, Sinφ= 0,31, P = 3,5 ∙ 0,95 =3,32 МВт,

Q = 3,5 ∙ 0,31 =1,085 МВАр.

 

 

3.2.4. Лампы накаливания мощностью 500 Вт каждая подключены равноме­р­но вдоль четырехпроводной воздушной линии 380/220 В длиной 300 м, выполненной алюминиевыми проводами сечением 25 мм². Нагрузка линии равна 15 кВт при cosφ =1. Определить потерю напряжения в линии (%).

Решение:

На 1 фазу приходится мощность Р=5 кВт, ток I = 5000/220=22,72 A.

Удельное активное сопротивление фазного провода r₀=1,17Ом/км.

Светильники распределены равномерно, расчетная длина l= 300/2=150 м.

Сопротивление провода R = r₀ ∙ l = 1,17 ∙ 0,15 = 0,18 Ом. Sinφ = 0.

Фазная потеря напряжения ΔU = I ∙ (R∙cosφ +X∙Sinφ) = 22,72 * 0,192 = 4,1 В или 4,1 ∙ 100 /220 = 1,9 %.

Линейная потеря напряжения ΔU= 4,1 ∙ √3= 7,1 В или 7,1∙ 100 /380=1,9%.