Реальные газы
Как известно, уравнение состояния устанавливает функциональную связь между давлением Р, объемом V, температурой T и числом молей газа в состоянии равновесия. Эта связь может выражаться не только в форме уравнения, но также графически или в виде таблиц, которые часто используются, особенно для практических целей. Самым простым и известным уравнением состояния является уравнение состояния идеального газа:

| 7.1.1 |
Реальные газы описываются уравнением состояния идеального газа только приближенно, и отклонения от идеального поведения становятся заметными при высоких давлениях и низких температурах, особенно когда газ близок к конденсации. Так, для газов с низкой температурой сжижения (He, H2, Ne и даже N2, O2, Ar, CO, CH4) при давлениях до 50 атм. отклонения не превышают 5 %, а при давлениях до 10 атм. – 2 %. Легко конденсирующиеся газы (CO2, SO2, Cl2, CH3Cl) уже при 1 атм. обнаруживают отклонения до 3 %.
Предпринималось много попыток для учета отклонений свойств реальных газов от свойств идеального газа путем введения различных поправок в уравнение состояния идеального газа.
Первая поправка в уравнении состояния идеального газа рассматривает собственный объем, занимаемый молекулами реального газа. В уравнении Дюпре (1864)
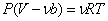 , ,
|
постоянная b учитывает собственный мольный объем молекул,  – число молей газа.
– число молей газа.
При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации (образование жидкости). Межмолекулярное притяжение эквивалентно существованию в газе некоторого внутреннего давления Р' (иногда его называют статическим давлением). Изначально величина Р' была учтена в общей форме в уравнении Гирна (1865):
 . .
|
Наибольшее распространение вследствие простоты и физической наглядности получило уравнение голландский физика Ван-дер-Ваальса. В 1873 г. он дал функциональную интерпретацию внутреннего давления. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван–дер–Ваальса) обратно пропорциональны шестой степени расстояния между ними, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:

|
Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.
Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.
Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, вводящая поправку на конечный диаметр молекулы и на притяжение молекул на больших расстояниях, тогда как в идеальных газах частицы считаются точечными и никак не взаимодействуют на расстоянии.
Термическое уравнение состояния
Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.
Для одного моля газа Ван-дер-Ваальса оно имеет вид:
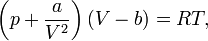
где
p — давление,
V — объём,
T — абсолютная температура,
R — универсальная газовая постоянная.
Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a учитывает притяжение молекул, поправка b — объём занимаемый молекулами.
Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

Внутренняя энергия (калорическое уравнение состояния)
Внутренняя энергия одного моля газа Ван-дер-Ваальса может быть вычислена так:
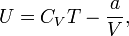
где CV — молярная теплоёмкость при постоянном объёме, которая предполагается не зависит от температуры.
Таким образом, внутренняя энергия газа Ван-дер-Ваальса есть функция и температуры, и объёма, вследствие чего с ростом последнего (а значит, и расстояния между молекулами), при T = const, внутренняя энергия газа растет.






