При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.
Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. 
, резистор сопротивлением R и катушку индуктивностью L. Под действием внешней э. д. с. в цепи течет постоянный ток
(внутренним сопротивлением источника тока пренебрегаем).
В момент времени t =0 отключим источник тока. Ток в катушке индуктивностью L начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции 
препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется закономОма I = s/R, или
(127.1)
Разделив в выражении (127.1) переменные, получим 
Интегрируя это уравнение по I (от I 0 до I) и t (от 0 до t), находим ln (I / I 0) = –Rt/L, или
(127.2)
где t= L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что t есть время, в течение которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше t и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При замыкании цепи помимо внешней э. д. с. возникает э. д. с. самоиндукции 
препятствующая, согласно правилу Ленца, возрастанию тока. По закону Ома, 
или
Введя новую переменную 
преобразуем это уравнение к виду
где t — время релаксации.
В момент замыкания (t =0) сила тока I = 0 и u = – . Следовательно, интегрируя по и (от – до IR– ) и t (от 0 до t), находим ln[(IR– )]/– = —t/t, или
(127.3)
где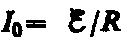 
— установившийся ток (при t ®¥).
Таким образом, в процессе включения источника тока нарастание силы тока в цепи задается функцией (127.3) и определяется кривой 2 на рис. 183. Сила тока возрастает от начального значения I= 0 и асимптотически стремится к установившемуся значению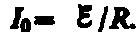 
. Скорость нарастания тока определяется тем же временем релаксации t=L/R, что и убывание тока. Установление тока происходит тем быстрее, чем меньше индуктивность цепи и больше ее сопротивление.
Оценим значение э.д.с. самоиндукции 
, возникающей при мгновенном увеличении сопротивления цепи постоянного тока от R 0 до R. Предположим, что мы размыкаем контур, когда в нем течет установившийся ток 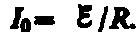. При размыкании цепи ток изменяется по формуле (127.2). Подставив в нее выражение для I 0 и t, получим
Э.д.с. самоиндукции
т. е. при значительном увеличении сопротивления цепи (R/R 0>>1), обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.
Магнитные моменты атомов.
Рассматривая действие магнитного поля на проводники с током и на движущиеся заряды, мы не интересовались процессами, происходящими в веществе. Свойства среды учитывались формально с помощью магнитной проницаемости m. Для того чтобы разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества.
Опыт показывает, что все вещества, помещенные в магнитное поле, намагничиваются. Рассмотрим причину этого явления с точки зрения строения атомов и молекул, положив в основу гипотезу Ампера, согласно которой в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах.
Для качественного объяснения магнитных явлений с достаточным приближением можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом (см. (109.2)) p m= IS n, модуль которого
(131.1)
где I=en — сила тока, n — частота вращения электрона по орбите, S — площадь орбиты. Если электрон движется по часовой стрелке (рис. 187), то ток направлен против часовой стрелки и вектор р m (в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона, как указано на рисунке.
С другой стороны, движущийся по орбите электрон обладает механическим моментом импульса L e, модуль которого,
(131.2)
где v = 2 pn, pr 2 = S. Вектор L e (его направление также определяется по правилу правого винта) называется орбитальным механическим моментом электрона.
Из рис. 187 следует, что направления р m и L e, противоположны, поэтому, учитывая выражения (131.1) и (131.2), получим
(131.3)
где величина
(131.4)
называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком «–», указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения v и r различны. Формула (131.4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит.
Экспериментальное определение гиромагнитного отношения проведено в опытах Эйнштейна и де Гааза* (1915), которые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничении во внешнем магнитном поле (по обмотке соленоида пропускался переменный ток с частотой, равной частоте крутильных колебаний стержня). При исследовании вынужденных крутильных колебаний стержня определялось гиромагнитное отношение, которое оказалось равным – (e/m). Таким образом, знак носителей, обусловливающих молекулярные токи, совпадал со знаком заряда электрона, а гиромагнитное отношение оказалось в два раза большим, чем введенная ранее величина g (см. (131.4)). Для объяснения этого результата, имевшего большое значение для дальнейшего развития физики, было предположено, а впоследствии доказано, что кроме орбитальных моментов электрон обладает собственным механическим моментом импульса L es, называемым спином. Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. В настоящее время установлено, что спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона L es, соответствует собственный (сотовый) магнитный момент р ms, пропорциональный L es и направленный в противоположную сторону:
(131.5)
Величина gs называется гиромагнитным отношением спиновых моментов.
Проекция собственного магнитного момента на направление вектора В может принимать только одно из следующих двух значений:
где ħ=h/ (2p) (h— постоянная Планка), m b— магнетон Бора, являющийся единицей магнитного момента электрона.
В общем случае магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Магнитный момент атома, следовательно, складывается из магнитных моментов входящих в его состав электронов и магнитного момента ядра (обусловлен магнитными моментами входящих в ядро протонов и нейтронов). Однако магнитные моменты ядер в тысячи раз меньше магнитных моментов электронов, поэтому ими пренебрегают. Таким образом, общий магнитный момент атома (молекулы) p a равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов:
(131.6)
