Движение заряженных частиц в магнитном поле.

Выражение для силы Лоренца позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Для вывода общих закономерностей будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол a между векторами v и В равен 0 или p. Тогда по формуле (114.1) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца F = Q [ vB ] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центро­стремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия QvB=mv²/r откуда

(115.1)

Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,

Подставив сюда выражение (115.1), получим

(115.2)

т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v<<c). На этом основано действие циклических ускорителей заряженных частиц.

Если скорость v заряженной частицы направлена под углом a к вектору В (рис. 170), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолиней­ного движения вдоль поля со скоростью v _|| =v cos a; 2) равномерного движения со скоростью v _^= v sin a по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить v на v _^= v sin a). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 170). Шаг винтовой линии

Подставив в последнее выражение (115.2), получим

Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость v заряженной частицы составляет угол a с направлением векто­ра В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то r и h уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.

Эффект Холла.

 

Эффект Холла* (1879) — это возникновение в металле (или полупроводнике) с током плотностью j, помещенном в магнитное поле В, электрического поля в направлении, перпендикулярном В и j.

 

Поместим металлическую пластинку с током плотностью j в магнитное поле В, перпендикулярное j (рис. 172). При данном направлении j скорость носителей тока в металле — электронов — направлена справа налево. Электроны испытывают дейст­вие силы Лоренца, которая в данном случае направлена вверх. Таким образом, у верхнего края пластинки возникнет повышенная концентрация электронов (он зарядится отрицательно), а у нижнего — их недостаток (зарядится положительно). В результате этого между краями пластинки возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность Е_B этого попереч­ного поля достигнет такой величины, что его действие на заряды будет уравновеши­вать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Тогда

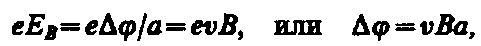
где а — ширина пластинки, Dj — поперечная (холловская) разность потенциалов.

Учитывая, что сила тока I=jS=nevS (S — площадь поперечного сечения пластинки толщиной d, п — концентрация электронов, v — средняя скорость упорядоченного движения электронов), получим

(117.1)

т. е. холловская поперечная разность потенциалов прямо пропорциональна магнитной индукции В, силе тока I и обратно пропорциональна толщине пластинки d. В формуле (117.1) R= 1 / (en) — постоянная Холла, зависящая от вещества. По измеренному значе­нию постоянной Холла можно: 1) определить концентрацию носителей тока в провод­нике (при известных характере проводимости и заряда носителей); 2) судить о природе проводимости полупроводников, так как знак постоянной Холла совпадает со знаком заряда е носителей тока. Эффект Холла поэтому — наиболее эффективный метод изучения энергетического спектра носителей тока в металлах и полупроводниках. Он применяется также для умножения постоянных токов в анало­говых вычислительных машинах, в измерительной технике (датчики Холла) и т. д.