В програмному середовищі MATLAB 5.3 (Release 11) та новіших версіях MATLAB функція fmins замінена функцією fminsearch.
Формати застосування функції fminsearch:
x=fminsearch('fun',x0) – починає з точки нульового наближення х0 та знаходить екстремум х критерію fun(х). х0 може бути число, вектор або матриця.
x=fminsearch('fun',x0,options) – виконує вищевказане із застосуванням опцій, введених у структурі options. Структура options містить такі поля:
Display – можливість виведення експериментів. Значення поля Display:
'off' – не виводити значення експериментів, 'iter' – виводити значення експериментів при кожній ітерації, 'final' – виводити лише значення кінцевого експерименту, 'notify' (за замовчуванням)– виводити результат лише коли функція не збігається.
якщо options(1)=0 – проміжні експерименти не виводяться.
MaxFunEvals – максимальна дозволена кількість експериментів.
MaxIter – максимальна дозволена кількість ітерацій.
TolX – точність вхідних параметрів х, при досягненні якої пошук екстремуму завершується.
[x,fval]=fminsearch('fun',x0,options) – виконує вищевказане та видає fval – значення критерію 'fun' в отриманому розв’язку x.
[x,fval,exitflag]=fminsearch('fun',x0,options) – виконує вищевказане та видає значення exitflag, яке показує умову виходу з ітераційного процесу функції fminsearch().
При exitflag>0 – ітераційний процес для заданого критерію 'fun' збігається до розв’язку x.
exitflag=0 означає, що максимальну кількість поставлених експериментів перевищено.
exitflag<0 означає, що ітераційний процес для заданого критерію 'fun' не збігається до розв’язку.
[x,fval,exitflag,output]=fminsearch('fun',x0,options) – виконує вищевказане та видає структуру output, у якій міститься інформація про оптимізацію:
output.algorithm – застосований алгоритм пошуку екстремуму;
output.funcCount – кількість поставлених експериментів;
output.iterations – кількість виконаних ітерацій.
Приклад застосуванням функції fminsearch для пошуку екстремуму дво-параметричного критерію, заданого функцією myfun(х), з виведенням значень експериментів при кожній ітерації, точністю вхідних параметрів 10-3 та виведенням знайдених координат екстремуму x, значення критерію в точці екстремуму fval, умови виходу з ітераційного процесу exitflag та кількості проведених експериментів:
[x,fval,exitflag,output]=fminsearch('myfun',[-3 0], optimset('Display','iter','TolX',1e-3));
x_min=x(1) % перша координата екстремуму
y_min=x(2) % друга координата екстремуму
f_min=fval % значення критерію в точці екстремуму
exitflag % умова виходу з ітераційного процесу
n=output.funcCount % кількість проведених експериментів
Порядок виконання лабораторної роботи
1. Засобами MATLAB побудувати графік поверхні заданої функції.
2. Для заданої функції написати програму реалізації методу Нелдера-Міда для пошуку мінімум в середовищі MATLAB.
3. Порівняти отримане значення мінімуму із значенням, отриманим із застосуванням функцій MATLAB fmins (fminsearch).
4. Зробити висновки.
5. Оформити звіт до лабораторної роботи.
Зміст звіту
1. Тема роботи.
2. Завдання та заданий критерій.
3. Графік поверхні критерію в просторі параметрів оптимізації
4. Блок-схема алгоритму пошуку мінімуму за методом Нелдера-Міда.
5. Програма пошуку мінімуму за методом Нелдера-Міда, а також із застосуванням функції fmins (fminsearch).
6. Порівняння отриманого значення мінімуму із значенням, отриманим з використанням функції fmins (fminsearch).
7. Висновки.
Варіанти завдань
| № варіанту | Критерій | Межі параметрів х, у |
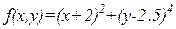
| х  [-300;300], у [-300;300], у  [-15;25] [-15;25]
| |
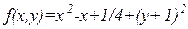
| х  [-8;8], у [-8;8], у  [-6;6] [-6;6]
| |
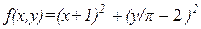
| х  [-10;10], у [-10;10], у  [-10;20] [-10;20]
| |
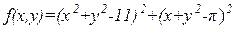
| х  [-10;10], у [-10;10], у  [-10;10] [-10;10]
| |
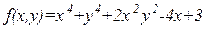
| х  [-10;10], у [-10;10], у  [-10;10] [-10;10]
| |
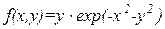
| х  [-3;3], у [-3;3], у  [-3;0] [-3;0]
| |
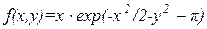
| х  [-4;0], у [-4;0], у  [-3;3] [-3;3]
| |
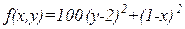
| х  [-100;100], у [-100;100], у  [-10;10] [-10;10]
| |
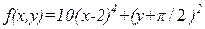
| х  [-4;8], у [-4;8], у  [-100;100] [-100;100]
| |
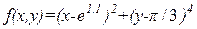
| х  [-70;70], у [-70;70], у  [-10;10] [-10;10]
| |
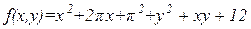
| х  [-20;10], у [-20;10], у  [-10;20] [-10;20]
| |
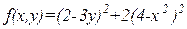
| х  [-10;10], у [-10;10], у  [-50;50] [-50;50]
| |
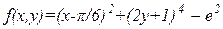
| х  [-300;300], у [-300;300], у  [-10;10] [-10;10]
| |
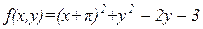
| х  [-15;10], у [-15;10], у  [-10;10] [-10;10]
|
Література
1. Уайлд Д.Д. Методы поиска экстремума. М.: Наука, 1967.
2. Потемкин В.Г. Система MATLAB 5. Справочное пособие. М.: ДИАЛОГ-
Додаток
Приклад оформлення звіту
Тема: Безумовна багатопараметрична оптимізація. Пошук екстремуму за симплексом. Метод Нелдера-Міда.
Завдання:
Побудувати графік поверхні та знайти мінімум критерію за методом Нелдера-Міда та за допомогою функції fmins (fminsearch) в середовищі MATLAB.
Заданий критерій:
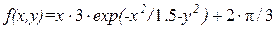
Виконання роботи
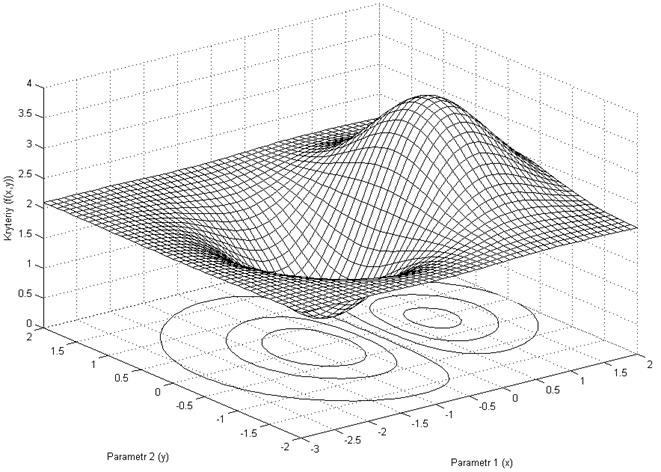
Рисунок 1. Графік поверхні та еквіпотенціальні лінії заданого критерію

Рисунок 2. Блок-схема алгоритму пошуку мінімуму за методом Нелдера-Міда
Програма пошуку мінімуму за методом Нелдера-Міда, а також із застосуванням функції fmins:
%lab4
clear,clc
% Побудова поверхні заданого критерію
[x,y]=meshgrid([-3:0.1:2],[-2:0.1:2]); z=l4f(x,y);
figure('name','Nelder-Mid','numbertitle','off','menubar','none', 'color','w');
h=surfc(x,y,z);set(h,'facecolor',[1 1 1],'edgecolor',[0 0 0])
xlabel('Parametr 1 (x)');ylabel('Parametr 2 (y)');zlabel('Kryteriy (f(x,y))');
hold on,
clear all
pause;
% Пошук мінімуму за методом Нелдера-Міда
disp('Пошук мінімуму за методом Нелдера-Міда')
l=1; %Початкова довжина ребра Симплекса
disp('Точність'), eps=0.001
al=1; be=0.5; ga=2; s1=0.9659; s2=0.2588;
x(1)=-3; y(1)=0; z(1)=l4f(x(1),y(1));
x(2)=x(1)+l*s2; y(2)=y(1)+l*s1; z(2)=l4f(x(2),y(2));
x(3)=x(1)+l*s1; y(3)=y(1)+l*s2; z(3)=l4f(x(3),y(3)); n=3;
figure(1),plot3(x,y,[0 0 0],'ok','markerfacecolor','k','markersize',3)
pause
while sqrt(sum((z-sum(z)/3).^2))/3>eps
[zs,j]=sort(z);
xl=x(j(1)); yl=y(j(1)); zl=zs(1);
xg=x(j(2)); yg=y(j(2)); zg=zs(2);
xh=x(j(3)); yh=y(j(3)); zh=zs(3);
xo=(xl+xg)/2; yo=(yl+yg)/2;
xr=(1+al)*xo-al*xh; yr=(1+al)*yo-al*yh; zr=l4f(xr,yr); n=n+1;
figure(1),plot3(xr,yr,0,'ok','markerfacecolor','k','markersize',3)
if zr<zl
xe=(1-ga)*xo+ga*xr; ye=(1-ga)*yo+ga*yr; ze=l4f(xe,ye); n=n+1;
figure(1),plot3(xe,ye,0,'ok','markerfacecolor','k','markersize',3)
if ze<zl, xh=xe; yh=ye; zh=ze;
else xh=xr; yh=yr; zh=zr;
end
else
if zr>zg
if zr<zh, xh=xr; yh=yr; zh=zr;
end
xc=(1-be)*xo+be*xh; yc=(1-be)*yo+be*yh; zc=l4f(xc,yc); n=n+1;
figure(1),plot3(xc,yc,0,'ok','markerfacecolor','k','markersize',3)
if zc>zh
xg=(xg+xl)/2; yg=(yg+yl)/2; zg=l4f(xg,yg);
xh=(xh+xl)/2; yh=(yh+yl)/2; zh=l4f(xh,yh); n=n+2;
figure(1),plot3([xg xh],[yg yh],[0 0],'ok','markerfacecolor','k','markersize',3)
else
xh=xc; yh=yc; zh=zc;
end
else
xh=xr; yh=yr; zh=zr;
end
end
x=[xl xg xh]; y=[yl yg yh]; z=[zl zg zh];
pause
end
line([xl xl],[yl yl],[0 2],'color','k');
disp('Мінімум знаходиться в точці з координатами'), x=xl, y=yl, z=zl
disp('Кількість експериментів'), n
% Пошук мінімуму за допомогою функції fmins()
disp('Застосування функції fmins()')
[x,options]=fmins('l4f1',[-3 0],[0 1 eps]);
x_min=x(1)
y_min=x(2)
z_min=l4f(x_min,y_min)
n=options(10)
Підпрограма із заданим критерієм для методу Нелдера-Міда:
function z=l4f(x,y);
z=x.*3.*exp(-x.^2./1.5-y.^2)+2*pi/3;
Підпрограма із заданим критерієм для функції fmins():
function z=l4f1(x);
z=x(1).*3.*exp(-x(1).^2./1.5-x(2).^2)+2*pi/3;
Порівняння отриманого значення мінімуму за методом Нелдера-Міда із значенням мінімуму, отриманим з використанням функції fmins() засобами MATLAB:
| Назва методу | Координати мінімуму критерію | Кількість експериментів n | ||
| xmin | ymin | fmin | ||
| Метод Нелдера-Міда | -0,8423 | -0,0396 | 0,5222 | |
| Функція fmins() | -0,8721 | 0,0007 | 0,5187 |
Висновок:
У результаті виконання цієї лабораторної роботи побудовано блок-схему алгоритму та складено програму пошуку мінімуму за методом Нелдера-Міда. Мінімальне значення критерію за методом Нелдера-Міда для заданої точності ε=0,001 досягається у точці з координатами xmin=-0,8423 ymin=-0,0396 після 26 поставлених експериментів. Мінімальне значення критерію, отримане за допомогою функції fmins, для заданої точності ε=0,001 досягається у точці з координатами xmin=-0,8721; ymin=0,0007 після 33 поставлених експериментів. Абсолютне відхилення значення критерію в точці мінімуму для методу Нелдера-Міда відносно функції fmins становить 0,5222-0,5187=0,0035, а відносне відхилення – (0,5222-0,5187)/0,5187·100%=0,6748%.






