Розв’язування одновимірних крайових задач методом скінченних елементів
Методичні матеріали
до лабораторної роботи № 5 з курсу:
“Математичне моделювання в САПР”
для студентів базового напрямку
6.0804 “Комп’ютерні науки”
Затверджено
на засіданні кафедри
“Системи автоматизованого проектування”
Протокол №
від
Львів 2008
Розв’язування одновимірних крайових задач методом скінченних елементів. Методичні матеріали до лабораторної роботи № 5 з курсу: “Математичне моделювання в САПР” для студентів базового напрямку 6.0804 “Комп’ютерні науки”.
Укладачі:
Макар В.М., доцент, к.т.н.
Юрчак І.Ю., доцент, к.т.н.
Відповідальний за випуск:
Лобур М.В., проф., д.т.н., завідувач кафедри САП
Рецензенти:
1. МЕТА РОБОТИ
Ознайомитися з методом скінченних елементів у формі Гальоркіна, способом побудови слабкої варіаційної форми та отримати практичні навики застосування методу до розв’язання одновимірних крайових задач на прикладі задачі Штурма-Ліувілля для звичайного диференціального рівняння другого порядку.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ
З математичної точки зору метод скінченних елементів (МСЕ) можна розглядати як процес Гальоркіна з спеціальним вибором базисних функцій, кожна з яких має так званий скінченний носій, тобто відмінна від нуля тільки в деякій невеликій підобласті всієї області визначення  вихідної задачі. В свою чергу, метод Гальоркіна можна трактувати як частковий випадок методу зважених нев’язок, в якому базисні та вагові функції співпадають. Тому для глибшого розуміння суті МСЕ коротко розглянемо спочатку основні ідеї цих методів
вихідної задачі. В свою чергу, метод Гальоркіна можна трактувати як частковий випадок методу зважених нев’язок, в якому базисні та вагові функції співпадають. Тому для глибшого розуміння суті МСЕ коротко розглянемо спочатку основні ідеї цих методів
МЕТОД ЗВАЖЕНИХ НЕВ’ЯЗОК
Розглянемо деяку крайову задачу в обмеженій області  з границею
з границею  , тобто задачу знаходження функції
, тобто задачу знаходження функції  , яка задовільняє диференціальне рівняння
, яка задовільняє диференціальне рівняння
 в
в  , (1)
, (1)
та граничні умови
 на
на  . (2)
. (2)
Тут  – заданий диференціальний оператор,
– заданий диференціальний оператор,  - заданий лінійний оператор,
- заданий лінійний оператор,  – задана функція. Апроксимацію
– задана функція. Апроксимацію  розв’язку
розв’язку  крайової задачі (1)-(2) будемо шукати у вигляді розкладу за базисними функціями
крайової задачі (1)-(2) будемо шукати у вигляді розкладу за базисними функціями
 , (3)
, (3)
де  - деякі коефіцієнти, які обчислюються таким чином, щоб отримати якомога краще наближення, а функція
- деякі коефіцієнти, які обчислюються таким чином, щоб отримати якомога краще наближення, а функція  і базисні функції
і базисні функції  вибрані таким чином, що
вибрані таким чином, що
 на
на  . (4)
. (4)
Умови (4) означають, що функція  задовільняє граничну умову (2), і, отже
задовільняє граничну умову (2), і, отже  , а базисні функції
, а базисні функції  на границі
на границі  рівні нулю. Базисні функції такого типу часто називаються функціями форми або пробними функціями. Такий спосіб вибору функції
рівні нулю. Базисні функції такого типу часто називаються функціями форми або пробними функціями. Такий спосіб вибору функції  та базисних функцій
та базисних функцій  автоматично забезпечує рівність
автоматично забезпечує рівність  на
на  для
для  . Це означає, що для отримання наближеного розв’язку крайової задачі (1)-(2) залишається забезпечити, щоб
. Це означає, що для отримання наближеного розв’язку крайової задачі (1)-(2) залишається забезпечити, щоб  задовільняла диференціальне рівняння (1).
задовільняла диференціальне рівняння (1).
Найбільш загальний спосіб визначення коефіцієнтів  у розкладі (3) полягає у використанні поняття нев’язки (відхилення) і називається методом зважених нев’язок. У загальному випадку нев’язка виникає тоді, коли ми намагаємося апроксимувати (наблизити) деяку функцію
у розкладі (3) полягає у використанні поняття нев’язки (відхилення) і називається методом зважених нев’язок. У загальному випадку нев’язка виникає тоді, коли ми намагаємося апроксимувати (наблизити) деяку функцію  в області
в області  іншою функцією
іншою функцією 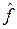 , і визначається вона наступним чином:
, і визначається вона наступним чином:
 . (5)
. (5)
У нашому випадку нев’язка виникає при підстановці розкладу (3) в диференціальне рівняння (1), оскільки  - апроксимація точного розв’язку
- апроксимація точного розв’язку  крайової задачі (1)-(2). В силу лінійності оператора
крайової задачі (1)-(2). В силу лінійності оператора  цю нев’язку можна записати у вигляді
цю нев’язку можна записати у вигляді
 . (6)
. (6)
Очевидно, що нам потрібно зменшити певним чином цю нев’язку, тобто забезпечити, щоб  всюди в
всюди в  . Для цього будемо вимагати рівності нулю відповідної кількості інтегралів по
. Для цього будемо вимагати рівності нулю відповідної кількості інтегралів по  від нев’язки
від нев’язки  , взятих з різними вагами, тобто
, взятих з різними вагами, тобто
 ,
,  , (7)
, (7)
де  - система лінійно незалежних вагових функцій. У силу довільності вибору вагових функцій
- система лінійно незалежних вагових функцій. У силу довільності вибору вагових функцій  рівності (7) будуть виконуватися тоді і лише тоді, коли
рівності (7) будуть виконуватися тоді і лише тоді, коли  при
при  , а це і означатиме, що апроксимація
, а це і означатиме, що апроксимація  буде задовільняти диференціальне рівняння (1) як завгодно точно. У цьому і полягає основна ідея методу зважених нев’язок. Рівності (7) утворюють систему рівнянь методу зважених нев’язок.
буде задовільняти диференціальне рівняння (1) як завгодно точно. У цьому і полягає основна ідея методу зважених нев’язок. Рівності (7) утворюють систему рівнянь методу зважених нев’язок.
Отже, для того, щоб апроксимація  була розв’язком рівняння (1) потрібно, щоб коефіцієнти
була розв’язком рівняння (1) потрібно, щоб коефіцієнти  визначалися з системи рівнянь методу зважених нев’язок (7).
визначалися з системи рівнянь методу зважених нев’язок (7).
МЕТОД ГАЛЬОРКІНА
На практиці можуть використовуватися різні системи вагових функцій  , що породжує різні методи на основі зважених нев’язок. У методі Гальоркіна, який є найбільш популярним варіантом методу зважених нев’язок, за вагові функції
, що породжує різні методи на основі зважених нев’язок. У методі Гальоркіна, який є найбільш популярним варіантом методу зважених нев’язок, за вагові функції  вибираються самі базисні функції
вибираються самі базисні функції  , тобто
, тобто
 . (8)
. (8)
Підстановка (6) і (8) в систему рівнянь методу зважених нев’язок (7) приводить до системи рівнянь Гальоркіна
 ,
,  , (9)
, (9)
розв’язавши яку відносно невідомих коефіцієнтів  , отримаємо систему лінійних алгебраїчних рівнянь (СЛАР)
, отримаємо систему лінійних алгебраїчних рівнянь (СЛАР)
 (10)
(10)
з коефіцієнтами  ,
,  . Легко бачити, що матриця
. Легко бачити, що матриця  СЛАР (10) є симетричною, що забезпечує методу Гальоркіна суттєві обчислювальні переваги.
СЛАР (10) є симетричною, що забезпечує методу Гальоркіна суттєві обчислювальні переваги.
Визначивши коефіцієнти  розкладу (3) з СЛАР (10), ми тим самим завершимо процес побудови апроксимації Гальоркіна
розкладу (3) з СЛАР (10), ми тим самим завершимо процес побудови апроксимації Гальоркіна  розв’язку
розв’язку  крайової задачі (1)-(2). Причому, нагадаємо, спосіб побудови
крайової задачі (1)-(2). Причому, нагадаємо, спосіб побудови  забезпечує апріорі виконання граничних умов (2). Спробуємо тепер послабити цю вимогу, оскільки вона суттєво обмежує вибір можливих типів базисних функцій.
забезпечує апріорі виконання граничних умов (2). Спробуємо тепер послабити цю вимогу, оскільки вона суттєво обмежує вибір можливих типів базисних функцій.
Отже, будемо тепер вважати, що розклад
 , (11)
, (11)
не задовільняє апріорі граничним умовам (2). Тоді до нев’язки в диференціальному рівнянні
 в
в  (12)
(12)
додається нев’язка в граничних умовах
 на
на  , (13)
, (13)
а система рівнянь Гальоркіна набуде вигляду
 ,
,  . (14)
. (14)
Підставивши (12)-(13) в (14) і розв’язавши відносно невідомих коефіцієнтів  , знову отримаємо СЛАР
, знову отримаємо СЛАР
 (15)
(15)
з коефіцієнтами
 ,
,  .
.
Розв’язок СЛАР (15) дає нам коефіцієнти  розкладу (11), тобто апроксимацію Гальоркіна
розкладу (11), тобто апроксимацію Гальоркіна  розв’язку
розв’язку  крайової задачі (1)-(2), яка вже апріорі не задовільняє точно граничні умови (2).
крайової задачі (1)-(2), яка вже апріорі не задовільняє точно граничні умови (2).
Однак, у цьому випадку виникає інша проблема, яка полягає у тому, що в рівняння Гальоркіна (14) можуть входити інтеграли, що містять похідні від  , вздовж границі
, вздовж границі  . Такі інтеграли, особливо для криволінійних границь, обчислити дуже складно. Позбавитись зазначених труднощей можна у такий спосіб. Повертаючись до рівняння Гальоркіна (14), необхідно зауважити, що в цьому рівнянні перший доданок
. Такі інтеграли, особливо для криволінійних границь, обчислити дуже складно. Позбавитись зазначених труднощей можна у такий спосіб. Повертаючись до рівняння Гальоркіна (14), необхідно зауважити, що в цьому рівнянні перший доданок
 ,
,
як правило, можна перетворити за допомогою правила інтегрування за частинами до виду
 , (16)
, (16)
де  - деякі лінійні диференціальні оператори нижчого порядку ніж вихідний оператор
- деякі лінійні диференціальні оператори нижчого порядку ніж вихідний оператор  . Тоді, для граничних умов певного типу, належно вибираючи базисну функцію
. Тоді, для граничних умов певного типу, належно вибираючи базисну функцію  можна добитися взаємного скорочення інтегралів вздовж границі, що містять
можна добитися взаємного скорочення інтегралів вздовж границі, що містять  та її похідні. Ці граничні умови називаються природніми, а отримане в результаті такого перетворення рівняння називається слабким формулюванням методу Гальоркіна або слабкою формою рівняння Гальоркіна. Інша перевага слабкої форми полягає в тому, що на базисні функції
та її похідні. Ці граничні умови називаються природніми, а отримане в результаті такого перетворення рівняння називається слабким формулюванням методу Гальоркіна або слабкою формою рівняння Гальоркіна. Інша перевага слабкої форми полягає в тому, що на базисні функції  накладаються слабші умови гладкості.
накладаються слабші умови гладкості.
Очевидно, що в методі Гальоркіна ключовою проблемою є проблема вибору системи базисних функцій. Причому вважається, що базисні функції визначені всюди в  , що є найголовнішим недоліком, оскільки таким чином обмежується як геометрична форма області
, що є найголовнішим недоліком, оскільки таким чином обмежується як геометрична форма області  , так і сам вигляд базисних функцій. Цей недолік усувається в методі скінченних елементів.
, так і сам вигляд базисних функцій. Цей недолік усувається в методі скінченних елементів.
МЕТОД СКІНЧЕННИХ ЕЛЕМЕНТІВ
В основі МСЕ лежать дві фундаментальні ідеї:
1) вихідна область  розбивається на ряд підобластей або елементів
розбивається на ряд підобластей або елементів  , що не перетинаються;
, що не перетинаються;
2) базисні функції  , що використовуються в процесі побудови апроксимації
, що використовуються в процесі побудови апроксимації  розв’язку
розв’язку  крайової задачі (1)-(2) є кусково визначеними, тобто вони відмінні від нуля тільки на деяких елементах
крайової задачі (1)-(2) є кусково визначеними, тобто вони відмінні від нуля тільки на деяких елементах  (про такі функції кажуть, що вони мають скінченний або фінітний носій, а самі функції так і називаються фінітні). Причому для різних елементів
(про такі функції кажуть, що вони мають скінченний або фінітний носій, а самі функції так і називаються фінітні). Причому для різних елементів  можуть використовуватися різні вирази для базисних функцій.
можуть використовуватися різні вирази для базисних функцій.
Як наслідок, сама апроксимація  є також кусковою, тобто може бути визначена окремо на кожному елементі. Більше того, інтеграли в системі рівнянь Гальоркіна (14) можуть бути обчислені простим сумуванням їх вкладів за кожним скінченним елементом
є також кусковою, тобто може бути визначена окремо на кожному елементі. Більше того, інтеграли в системі рівнянь Гальоркіна (14) можуть бути обчислені простим сумуванням їх вкладів за кожним скінченним елементом  :
:
 ,
,  , (17)
, (17)
при умові, що
 .
.
Тут  - загальна кількість скінченних елементів (СЕ), на які розбивається вся область
- загальна кількість скінченних елементів (СЕ), на які розбивається вся область  ,
,  - та частина границі елемента
- та частина границі елемента  , що лежить на границі
, що лежить на границі  .
.
Очевидно, що СЕ  повинні мати досить просту геометричну форму. Так, для одновимірного випадку СЕ – це відрізки, для 2D областей – трикутники або чотирикутники, а для 3D областей – тетраедри або паралепіпеди. З кожним елементом
повинні мати досить просту геометричну форму. Так, для одновимірного випадку СЕ – це відрізки, для 2D областей – трикутники або чотирикутники, а для 3D областей – тетраедри або паралепіпеди. З кожним елементом  пов’язується набір точок, які називаються вузлами. У найпростішому випадку ці вузли розташовані у вершинах елемента, у складніших випадках вони можуть знаходитися всередині елемента (в одновимірному випадку) або на лініях (поверхнях) спряження суміжних елементів. Вузли та елементи нумеруються, причому спосіб нумерації впливає на структруру матриці результуючої СЛАР і, відповідно, на обчислювальні характеристики.
пов’язується набір точок, які називаються вузлами. У найпростішому випадку ці вузли розташовані у вершинах елемента, у складніших випадках вони можуть знаходитися всередині елемента (в одновимірному випадку) або на лініях (поверхнях) спряження суміжних елементів. Вузли та елементи нумеруються, причому спосіб нумерації впливає на структруру матриці результуючої СЛАР і, відповідно, на обчислювальні характеристики.
Тоді апроксимація  розв’язку крайової задачі (1)-(2) може бути записана у стандартній формі (11), якщо кожна базисна функція
розв’язку крайової задачі (1)-(2) може бути записана у стандартній формі (11), якщо кожна базисна функція  асоціюється з одним вузлом
асоціюється з одним вузлом  , причому сама базисна функція
, причому сама базисна функція  будується таким чином, щоб її значення було рівне одиниці лише у вузлі
будується таким чином, щоб її значення було рівне одиниці лише у вузлі  та нулю у всіх інших вузлах, тобто
та нулю у всіх інших вузлах, тобто
 . (18)
. (18)
У силу цієї властивості коефіцієнти  у розкладі (11) набувають цілком конкретного фізичного змісту: вони рівні значенню апроксимації
у розкладі (11) набувають цілком конкретного фізичного змісту: вони рівні значенню апроксимації  у вузлах, тобто
у вузлах, тобто  , де
, де  - значення
- значення  у вузлі
у вузлі  . Крім того, властивість (18) означає також, що базисна функція
. Крім того, властивість (18) означає також, що базисна функція  відмінна від нуля лише на тих СЕ, які містять вузол
відмінна від нуля лише на тих СЕ, які містять вузол  . Це в свою чергу і означає, що апроксимація
. Це в свою чергу і означає, що апроксимація  кусково визначена, тобто на кожному СЕ
кусково визначена, тобто на кожному СЕ  може бути виражена за допомогою лише тих базисних функцій
може бути виражена за допомогою лише тих базисних функцій  , вузли яких належать цьому елементу. Так, наприклад, в одновимірному випадку на кожному елементі
, вузли яких належать цьому елементу. Так, наприклад, в одновимірному випадку на кожному елементі  з вузлами
з вузлами  глобальна апроксимація
глобальна апроксимація  виду (11) може бути виражена за допомогою лише двох базисних функцій елемента
виду (11) може бути виражена за допомогою лише двох базисних функцій елемента  та вузлових значень
та вузлових значень  так:
так:
 . (19)
. (19)
Отже, кускова визначеність апроксимації  є наслідком кускової визначеності базисних функцій
є наслідком кускової визначеності базисних функцій  . Але, з іншого боку, кускова визначеність базисних функцій
. Але, з іншого боку, кускова визначеність базисних функцій  означає, що похідні від них будуть мати розриви. Тоді цілком логічно виникає питання, а наскільки допустимо використовувати такі функції в системі рівнянь Гальоркіна (14), які містять похідні від них під знаком інтегралу? З математичної точки зору, це означає, що потрібно встановити так звані умови гладкості на базисні функції, виконання яких гарантуватиме, що під інтегралами системи рівнянь Гальоркіна (14) не будуть виникати різного роду невизначеності. Ці умови гладкості визначаються порядком похідних від базисних функцій. Тут доречно нагадати, що цей порядок похідних можна знизити використовуючи слабку форму рівнянь Гальоркіна. Самі умови гладкості математично виражаються таким чином: якщо рівняння (14) містять похідні порядку
означає, що похідні від них будуть мати розриви. Тоді цілком логічно виникає питання, а наскільки допустимо використовувати такі функції в системі рівнянь Гальоркіна (14), які містять похідні від них під знаком інтегралу? З математичної точки зору, це означає, що потрібно встановити так звані умови гладкості на базисні функції, виконання яких гарантуватиме, що під інтегралами системи рівнянь Гальоркіна (14) не будуть виникати різного роду невизначеності. Ці умови гладкості визначаються порядком похідних від базисних функцій. Тут доречно нагадати, що цей порядок похідних можна знизити використовуючи слабку форму рівнянь Гальоркіна. Самі умови гладкості математично виражаються таким чином: якщо рівняння (14) містять похідні порядку  , то базисні функції повинні належати класу гладкості
, то базисні функції повинні належати класу гладкості  , тобто мати кусково-неперервно диференційовані похідні до порядку
, тобто мати кусково-неперервно диференційовані похідні до порядку  включно.
включно.
Властивість (18) означає, також, що якщо базисні функції  будувати у вигляді поліномів певного степеня, то апроксимація
будувати у вигляді поліномів певного степеня, то апроксимація  вигляду (11) являє собою інтерполяційний поліном розв’язку
вигляду (11) являє собою інтерполяційний поліном розв’язку  крайової задачі (1)-(2). Однозначність визначення полінома на кожному СЕ забезпечується тим, що у заданих вузлах у ролі невідомих параметрів фіксуються значення полінома або значення полінома і деяких його похідних. Необхідна гладкість апроксимації
крайової задачі (1)-(2). Однозначність визначення полінома на кожному СЕ забезпечується тим, що у заданих вузлах у ролі невідомих параметрів фіксуються значення полінома або значення полінома і деяких його похідних. Необхідна гладкість апроксимації  у всій області
у всій області  забезпечується тим, що значення відповідних параметрів у спільних вузлах суміжних елеметів співпадають. Поліноміальний вигляд базисних функцій забезпечує МСЕ високу ефективність та простоту обчислень, а також дозволяє отримати апріорні оцінки похибки апроксимації. Більше того, математичні дослідження МСЕ показали, що кусково-поліноміальні базисні функції за умови достатньої гладкості шуканого розв’язку забезпечують побудову наближеного розв’язку майже довільної точності, якщо ввести достатню кількість скінченних елементів або при заданому розбитті використати поліноми вищого порядку.
забезпечується тим, що значення відповідних параметрів у спільних вузлах суміжних елеметів співпадають. Поліноміальний вигляд базисних функцій забезпечує МСЕ високу ефективність та простоту обчислень, а також дозволяє отримати апріорні оцінки похибки апроксимації. Більше того, математичні дослідження МСЕ показали, що кусково-поліноміальні базисні функції за умови достатньої гладкості шуканого розв’язку забезпечують побудову наближеного розв’язку майже довільної точності, якщо ввести достатню кількість скінченних елементів або при заданому розбитті використати поліноми вищого порядку.
Підсумовуючи, можна виділити такі етапи розв’язання крайових задач за допомогою МСЕ:
1) дискретизація області  визначення задачі, яка включає задання кількості, розмірів та геометричної форми СЕ;
визначення задачі, яка включає задання кількості, розмірів та геометричної форми СЕ;
2) побудова апроксимації невідомого розв’язку шляхом розкладу за базисними функціями та отримання слабкої форми системи рівнянь Гальоркіна;
3) побудова фінітних базисних функцій у вигляді кусково визначених поліномів певного порядку, який визначається потрібними умовами гладкості розв’язку;
4) підстановка базисних функцій у слабку форму і отримання результуючої СЛАР шляхом побудови локальних матриць на кожному елементі та їх асемблювання у глобальні матриці СЛАР;
5) врахування граничних умов;
6) розв’язання СЛАР та оцінка точності отриманого наближеного розв’язку.






