Пусть закрепленная одним концом пружина лежит свободно на гладком столе. Под действием внешней силы F, направленной по оси x, пружина растянулась, ее удлинение составило x. При деформации в пружине возникают силы упругости F упр, равные по величине и противоположные по направлению приложенной внешней силе: F упр = - F.
Закон Гука в данном случае имеет вид: 
. Обычно индекс у силы упругости опускают и закон Гука записывается в виде:
.
Здесь Fx - проекция упругой силы на ось x. Коэффициент k называется жесткостью пружины.
Однородные стержни ведут себя при одностороннем сжатии подобно пружине. Деформация приводит к возникновению в стержне упругих сил.
Эти силы принято характеризовать напряжением s, которое определяют как модуль
силы, приходящейся на единицу площади поверхности:
Здесь S - площадь поперечного сечения стержня, Fn - составляющая силы, перпендикулярная к площадке, на которую она действует, поэтому такое напряжение называется нормальным. Обозначив относительное удлинение стержня как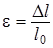 
, запишем закон Гука в виде:
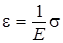или 
.
Величина Е характеризует упругие свойства материала стержня и называется модулем Юнга.
Силами упругости являются такие силы, как сила нормального давления N и сила натяжения нити Т.
Деформации сдвига
Рассмотрим прямоугольный брусок, закрепленный неподвижно нижней гранью. Под действием касательной (тангенциальной) силы Ft, приложенной к верхней грани, брусок получает деформацию, называемую сдвигом.
Величина, равная тангенсу угла сдвига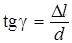 
, называется относительным сдвигом. При упругих деформациях угол g бывает очень мал, поэтому относительный сдвиг определяется формулой: 
.
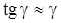Деформация сдвига приводит к возникновению в каждой точке бруска тангенциального напряжения st, которое определяется как модуль силы, действующей на единицу площади поверхности:
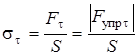
Закон Гука для сдвиговых деформаций имеет вид:
,
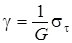где G зависит только от свойств материала и называется модулем сдвига. Для большинства однородных изотропных тел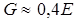 
. Модуль Юнга и модуль сдвига измеряются в Паскалях.
Деформации кручения
Рассмотрим стержень в виде прямого кругового цилиндра радиуса r, верхнее основание которого закреплено, а в некотором произвольном сечении, расположенном на расстоянии L от закрепленного, приложена пара касательных сил Ft, момент которых по величине равен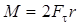 
и направлен вдоль оси цилиндра.
Под действием вращающего момента все сечения цилиндра поворачиваются на угол j тем больший, чем дальше эти сечения расположены от закрепленного основания. При упругих деформациях угол кручения пропорционален вращающему моменту:
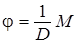
Деформации кручения являются частным случаем сдвиговых деформаций, поскольку любое нижнее сечение испытывает сдвиг относительно верхнего. Поэтому модуль кручения можно выразить через модуль сдвига. Детальный расчет приводит к следующему выражению:
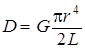
Силы трения
Трение, возникающее при относительном перемещении сухих поверхностей твердого тела, называется сухим трением. Различают три вида сухого
трения: трение покоя, скольжения и качения..
Если на тело действует сила, но тело сохраняет состояние покоя (неподвижно относительно поверхности, на которой оно находится), то это означает, что на тело одновременно действует сила, равная по величине и противоположная по направлению, - сила трения покоя. При увеличении силы, если тело сохраняет состояние покоя, то увеличивается и сила трения покоя. Сила трения покоя всегда равна по величине и противоположна по направлению внешней действующей силе.
Сила трения скольжения возникает при скольжении данного тела по поверхности другого тела. Чаще всего силу трения скольжения принимают равной максимальной силе трения покоя:
,
где m - коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей (в частности, от их шероховатости), N - сила нормального давления, прижимающая трущиеся поверхности друг к другу.
Сила трения качения мала по сравнению силой трения скольжения.
При движении твердого тела в жидкости или газе на него действует сила, препятствующая движению. При малых скоростях сила сопротивления пропорциональна первой степени скорости тела:
,
при больших скоростях - приблизительно пропорциональна квадрату скорости:
.
Коэффициенты сопротивления k 1 и k 2, а также область скоростей, в которой осуществляется переход от линейного закона к квадратичному, в сильной степени зависят от формы и размеров тела, направления его движения, состояния поверхности тела и от свойств окружающей среды.
Краткие сведения о законах, описывающих разные виды взаимодействий, приведены в таблице 4.
Информация о силах Таблица 4
| Происхождение сил | Законы сил |
| Гравитационное притяжение материальных точек с массами m 1 и m 2, находящихся на расстоянии r | Закон всемирного тяготения
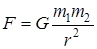(G - гравитационная постоянная)
|
| Действие Земли с точки зрения наблюдателя, находящегося на Земле | Сила тяжести
|
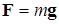
| Действие растянутой или сжатой пружины жесткостью k | Закон Гука
(x - смещение от положения равновесия)
|
| Взаимодействие при контакте поверхностей твердых тел | Сила нормального давления N |
Сила трения покоя  или
| |
сила трения скольжения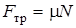 
| |
| Сопротивление движению твердого тела относительно жидкости или газа | Сила вязкого трения при малых
скоростях 
|
Сила вязкого трения при больших
скоростях 
| |
| Выталкивающая сила, действующая на твердое тело, находящееся в жидкости или газе | Закон Архимеда 
(m - масса вытесненной жидкости или газа)
|
| Действие электрического поля на заряд q | 
(E -напряженность поля)
|
| Действие магнитного поля на движущийся заряд q | Сила Лоренца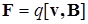 
(B - вектор магнитной индукции)
|
Законы динамики
Законы Ньютона
Прежде всего напомним законы Ньютона. Они применяются при описании движения материальной точки или поступательного движения твердого тела.
В первом законе Ньютона утверждается, что существуют такие системы отсчета, относительно которых тело находится в состоянии покоя или прямолинейного равномерного движения, если на него не действуют силы или равнодействующая всех сил равна нулю. Такие системы отсчета называются инерциальными (ИСО). Любая система отсчета, движущаяся с постоянной скоростью относительно ИСО, также является инерциальной.
Во втором законе Ньютона устанавливается связь между воздействием на тело - силой и реакцией на воздействие, которая проявляется в изменении скорости, т.е. в ускорении:
,
т.е. в инерциальных системах отсчета произведение массы тела на его ускорение равно силе, действующей на это тело. Если сил несколько, то под F понимается равнодействующая сила.
В третьем законе Ньютона утверждается, что действие равно противодействию, а именно, два тела взаимодействуют с силами, равными по величине, и противоположными по направлению:
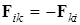
Отметим, что эти силы приложены к разным телам и никогда не компенсируют друг друга.
