(СИСТЕМЫ СО МНОГИМИ ВЫХОДАМИ)
Пусть как и прежде  – входной,
– входной,  – выходной и
– выходной и 
 – промежуточные сигналы четырехполюсника. Тогда система дифференциальных уравнений четырехполюсника может быть записана в виде
– промежуточные сигналы четырехполюсника. Тогда система дифференциальных уравнений четырехполюсника может быть записана в виде
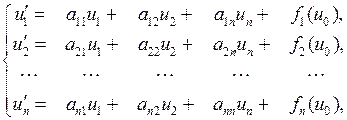 (1.67)
(1.67)
где  – правые части, зависящие только от входного сигнала
– правые части, зависящие только от входного сигнала  . Уравнения (1.67) для компактности можно записать в векторной форме
. Уравнения (1.67) для компактности можно записать в векторной форме
 , (1.68)
, (1.68)
где
 .
.
Решение системы (1.68) состоит из совокупности векторов-решений 
 ,
,
(где  – произвольные постоянные) однородной системы
– произвольные постоянные) однородной системы
 (1.69)
(1.69)
и частного вектора-решения 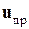 неоднородного уравнения (1.68)
неоднородного уравнения (1.68)
 .
.
Здесь
 ,
,
где  ,
, 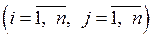 – частные решения. Индекс
– частные решения. Индекс  соответствует номеру искомой переменной, а индекс
соответствует номеру искомой переменной, а индекс  – номеру частного решения.
– номеру частного решения.
1.9.1. РЕШЕНИЕ ОДНОРОДНОЙ СИСТЕМЫ
(СВОБОДНЫЙ РЕЖИМ)
Вид частных решений системы (1.69) определяет характеристическое уравнение
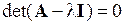 , (1.70)
, (1.70)
где  – единичная матрица. В развернутой форме (1.70) примет следующий вид:
– единичная матрица. В развернутой форме (1.70) примет следующий вид:
 . (1.71)
. (1.71)
А. Корни характеристического уравнения
различные и действительные
В этом случае корням 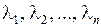 соответствуют частные решения
соответствуют частные решения
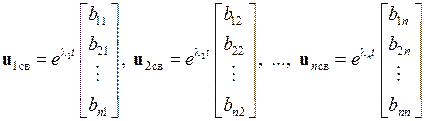 ,
,
где 
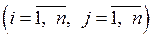 – произвольные постоянные.
– произвольные постоянные.
Пример 1.13. Найти вид свободного решения системы
 (1.72)
(1.72)
Характеристическое уравнение системы имеет вид
 .
.
Отсюда 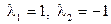 . Этим корням соответствуют частные решения
. Этим корням соответствуют частные решения
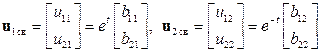 .
.
Для определения вида свободной составляющей, соответствующей корню  , подставим
, подставим 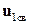 в (1.72)
в (1.72)

Отсюда  .
.
Второе уравнение является следствием первого, поэтому один из коэффициентов можно взять произвольно; примем  . Тогда
. Тогда  . Следовательно, первое частное вектор-решение будет
. Следовательно, первое частное вектор-решение будет
 .
.
В случае корня  поступим аналогично предыдущему
поступим аналогично предыдущему

откуда  ,
,  .
.
Второе уравнение снова является следствием первого. Тогда произвольно примем  . Следовательно, второе частное вектор-решение будет
. Следовательно, второе частное вектор-решение будет
 .
.
Таким образом, общее решение системы (1.72) имеет следующий вид:

или

Б. Корни характеристического уравнения действительные, кратные
Пусть  является r -кратным корнем характеристического уравнения (1.71). В этом случае также имеем п частных решений
является r -кратным корнем характеристического уравнения (1.71). В этом случае также имеем п частных решений
 ,
,
где коэффициенты 
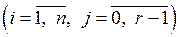 , как и прежде, – произвольные постоянные.
, как и прежде, – произвольные постоянные.
Пример 1.14. Найти общее решение системы
 (1.73)
(1.73)
Характеристическое уравнение системы имеет вид
 .
.
Его корни  . Вектор-решение запишется как
. Вектор-решение запишется как
 . (1.74)
. (1.74)
Коэффициенты  определяются подстановкой (1.74) в (1.73) аналогично примеру 1.13
определяются подстановкой (1.74) в (1.73) аналогично примеру 1.13
 . (1.75)
. (1.75)
Приравнивая коэффициенты при одинаковых степенях  в системе (1.75), получим следующие системы для определения коэффициентов
в системе (1.75), получим следующие системы для определения коэффициентов  :
:
 , (1.76)
, (1.76)
 . (1.77)
. (1.77)
Поскольку уравнения системы (1.77) линейно зависимы, то коэффициент  может быть произвольным, например
может быть произвольным, например  . Тогда
. Тогда 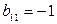 , а из (1.76) следует, что
, а из (1.76) следует, что  . Из-за линейной зависимости уравнений (1.76) коэффициенты
. Из-за линейной зависимости уравнений (1.76) коэффициенты 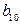 и
и  также произвольны; пусть
также произвольны; пусть  , тогда
, тогда  . Таким образом, искомое свободное решение будет равно
. Таким образом, искомое свободное решение будет равно
 .
.
В. Корни характеристического уравнения комплексные
Пусть таким корнем является  , тогда ему соответствует сопряженный корень
, тогда ему соответствует сопряженный корень  .
.
Общее решение системы в этом случае ищется в следующем
виде:
 , (1.78)
, (1.78)
где  и
и  – вещественная и мнимая части частного решения, соответствующего одному из корней (например, корню
– вещественная и мнимая части частного решения, соответствующего одному из корней (например, корню  )
)
 , (1.79)
, (1.79)
где коэффициенты  в общем случае будут комплексными.
в общем случае будут комплексными.
Пример 1.15. Найти свободное решение системы
 (1.80)
(1.80)
Характеристическое уравнение системы имеет вид
 ;
;
его корни 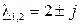 .
.
Найдем частное решение для одного из корней, например для
 .
.
Согласно (1.79)
 . (1.81)
. (1.81)
Подставим (1.81) в (1.80) и сократим на 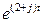
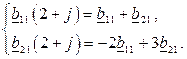 (1.82)
(1.82)
Отсюда следует, что
 ,
,
причем  – произвольное число (из-за линейной зависимости системы (1.82)).
– произвольное число (из-за линейной зависимости системы (1.82)).
Пусть  , тогда
, тогда  . Частное решение (1.81) будет иметь следующий вид:
. Частное решение (1.81) будет иметь следующий вид:
 .
.
В соответствии с (1.78)
 .
.
1.9.2. ОПРЕДЕЛЕНИЕ ЧАСТНОГО РЕШЕНИЯ
НЕОДНОРОДНОЙ СИСТЕМЫ (ПРИНУЖДЕННЫЙ РЕЖИМ)
1. Если правая часть 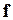 системы (1.68) состоит из функций
системы (1.68) состоит из функций
 , (1.83)
, (1.83)
то частное решение системы будет содержать составляющие вида
 , (1.84)
, (1.84)
где  – кратность корня
– кратность корня  (если среди корней нет
(если среди корней нет  , то
, то  ). Здесь
). Здесь  – порядок системы.
– порядок системы.
2. Если правая часть (1.68) содержит функции

или
 ,
,
то принужденное решение будет иметь следующие составляющие:
 ,
,
где  .
.
Пример 1.16. Найти частное решение системы
 (1.85)
(1.85)
Нетрудно видеть, что эта система заимствована из примера 1.13. Корни характеристического уравнения  и
и  не совпадают с показателями степеней экспонент правых частей:
не совпадают с показателями степеней экспонент правых частей: 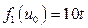 ,
,  . Согласно (1.83) и (1.84) можно записать
. Согласно (1.83) и (1.84) можно записать
 . (1.86)
. (1.86)
Для определения постоянных подставим (1.86) в (1.85)

Приведя одинаковые члены, получим
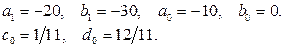
Тогда принужденное решение системы будет иметь следующий вид:
 .
.
* Переменными состояния являются ток в индуктивности и напряжение на емкости (более подробно см. разд. 1.8.2).






