КЛАССИЧЕСКИМ МЕТОДОМ
1.8.1. ПРЕДШЕСТВУЮЩИЙ
И ПОСЛЕКОММУТАЦИОННЫЙ РЕЖИМЫ
Примем момент скачкообразного изменения входного сигнала  за нуль. Тогда по левую сторону от
за нуль. Тогда по левую сторону от  будет находиться предшествующий режим, а по правую – послекоммутационный (режим после изменения
будет находиться предшествующий режим, а по правую – послекоммутационный (режим после изменения  или правой части
или правой части  уравнения (1.24)). Поскольку в точке
уравнения (1.24)). Поскольку в точке  сходятся два процесса, то она принадлежит обоим процессам и имеет особый статус. Для внесения определенности в статус этой точки в электротехнике момент коммутации на оси времени
сходятся два процесса, то она принадлежит обоим процессам и имеет особый статус. Для внесения определенности в статус этой точки в электротехнике момент коммутации на оси времени 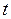 представляют как совокупность двух точек:
представляют как совокупность двух точек:  и
и  . Точка
. Точка  принадлежит предшествующему режиму, а
принадлежит предшествующему режиму, а  – послекоммутационному. Соответственно представляются и все остальные величины, характеризующие процесс. Например, значение электрической величины
– послекоммутационному. Соответственно представляются и все остальные величины, характеризующие процесс. Например, значение электрической величины  в момент
в момент  определяется как предельное значение
определяется как предельное значение  при подходе к точке
при подходе к точке  слева
слева

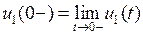 ,
,
а в момент  – как предельное приближение справа по оси
– как предельное приближение справа по оси 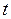 (рис. 1.10)
(рис. 1.10)
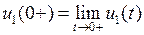 .
.
1.8.2. ЗАКОНЫ КОММУТАЦИИ
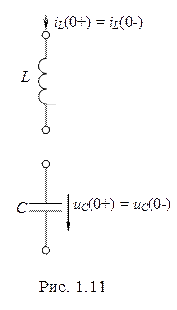 Основной закон коммутации можно выразить следующим образом: переменные состояния системы не могут изменяться скачком.
Основной закон коммутации можно выразить следующим образом: переменные состояния системы не могут изменяться скачком.
В электротехнике переменными состояния являются потокосцепление  (ток в индуктивности
(ток в индуктивности  при
при  ) и заряд
) и заряд  (напряжение на емкости
(напряжение на емкости  при
при  ). Применительно к ним законы коммутации формулируются следующим образом (рис. 1.11):
). Применительно к ним законы коммутации формулируются следующим образом (рис. 1.11):
1. Потокосцепление  (ток в индуктивности
(ток в индуктивности  ) не может изменяться скачком, т.е. в момент коммутации выполняются следующие равенства:
) не может изменяться скачком, т.е. в момент коммутации выполняются следующие равенства:
 , (1.40)
, (1.40)
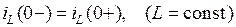 . (1.41)
. (1.41)
2. Заряд  конденсатора (напряжение на емкости
конденсатора (напряжение на емкости  ) не может изменяться скачком, т.е. в момент коммутации справедливы следующие зависимости:
) не может изменяться скачком, т.е. в момент коммутации справедливы следующие зависимости:
 , (1.42)
, (1.42)
 . (1.43)
. (1.43)
1.8.3. ОБОБЩЕННЫЕ ЗАКОНЫ КОММУТАЦИИ
Есть особые случаи, когда законы (1.40) - (1.43) нарушаются. Для этих случаев формулируют обобщенные законы коммутации.
1. Если в схеме после коммутации образовался контур, состоящий из индуктивных элементов или из индуктивных элементов и источников тока, то в момент коммутации алгебраическая сумма потокосцеплений упомянутого контура непрерывна
 . (1.44)
. (1.44)
Потокосцепление индуктивности берется со знаком "+", если направление обхода контура совпадает с принятым направлением тока в индуктивности.
 Пример 1.9. Определить токи в индуктивностях в момент
Пример 1.9. Определить токи в индуктивностях в момент  , если
, если  (рис. 1.12).
(рис. 1.12).
Ток  . После размыкания ключа
. После размыкания ключа  индуктивность
индуктивность  стремится поддерживать ток
стремится поддерживать ток  , а индуктивность
, а индуктивность  – ток
– ток  . Поскольку индуктивности составляют последовательную цепь, то по закону Кирхгофа их токи в момент
. Поскольку индуктивности составляют последовательную цепь, то по закону Кирхгофа их токи в момент  должны быть одинаковы:
должны быть одинаковы:  , что нарушает закон (1.41), так как
, что нарушает закон (1.41), так как  , а
, а  . Поэтому нужно применить обобщенный закон (1.44)
. Поэтому нужно применить обобщенный закон (1.44)
 .
.
Подставим известные величины, тогда получим систему уравнений

откуда следует, что

2. Если в схеме после коммутации образовались контуры, состоящие только из емкостей или из емкостей и источников напряжения, то в момент коммутации алгебраическая сумма зарядов емкостей, присоединенных к общему узлу, непрерывна
 . (1.45)
. (1.45)
Знак заряда считается положительным, если напряжение на емкости направлено от узла.

Пример 1.10. Найти напряжения на конденсаторах в момент  , если
, если  и
и  (рис. 1.13).
(рис. 1.13).
В этой схеме не выполняются законы (1.42) и (1.43). Применим обобщенный закон (1.45) для узла а, получим
 . (1.46)
. (1.46)
Кроме того, должен выполняться второй закон Кирхгофа
 . (1.47)
. (1.47)
Подставим в (1.46) и (1.47) известные значения

Совместное решение уравнений дает следующий результат:
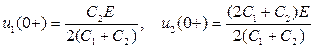 .
.
1.8.4. НАЧАЛЬНЫЕ УСЛОВИЯ.
ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ИНТЕГРИРОВАНИЯ
Решение неоднородного уравнения (1.24) состоит из совокупности частных решений
 .
.
Принужденная составляющая определяется непосредственно из уравнения (1.25) по виду правой части (п. 1.7.2). Для определения постоянных интегрирования необходимо составить систему из  уравнений
уравнений
 (1.48)
(1.48)
Величины  ,
, 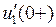 ,...,
,...,  называются начальными условиями; они определяются из уравнений четырехполюсника, составленных по законам Кирхгофа после коммутации с учетом переменных состояния.
называются начальными условиями; они определяются из уравнений четырехполюсника, составленных по законам Кирхгофа после коммутации с учетом переменных состояния.
1.8.5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ ЧЕТЫРЕХПОЛЮСНИКА
НА ВХОДНОЕ ВОЗДЕЙСТВИЕ
Для определения реакции выполняются следующие действия:
1. Составляется система дифференциальных уравнений четырехполюсника и преобразуется к уравнению типа "вход-выход".
2. Определяется решение однородного уравнения (свободный режим):
а) формируется характеристическое уравнение и находятся его корни;
б) по корням характеристического уравнения определяется вид общего решения  .
.
3. Определяется частное решение неоднородного уравнения (принужденный режим):
а) записывается правая часть уравнения  ;
;
б) по виду  и с учетом корней характеристического уравнения определяется вид частного решения
и с учетом корней характеристического уравнения определяется вид частного решения  ;
;
в) частное решение  подставляется в неоднородное уравнение, и тем самым определяются произвольные постоянные, присутствующие в
подставляется в неоднородное уравнение, и тем самым определяются произвольные постоянные, присутствующие в  .
.
4. Составляется система уравнений для определения произвольных постоянных общего решения  однородного
однородного
уравнения.
5. По схеме до коммутации определяются переменные состояния в момент  .
.
6. Записываются уравнения четырехполюсника после коммутации для  . Используя переменные состояния и уравнения системы, определяются необходимые начальные условия:
. Используя переменные состояния и уравнения системы, определяются необходимые начальные условия:  ,
, 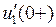 ,...,
,...,  , где
, где  число произвольных постоянных, подлежащих определению.
число произвольных постоянных, подлежащих определению.
 Пример 1.12. Определить реакцию четырехполюсника (рис. 1.14) на входное воздействие
Пример 1.12. Определить реакцию четырехполюсника (рис. 1.14) на входное воздействие 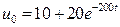 . Параметры цепи:
. Параметры цепи: 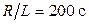 ,
, 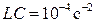 . До коммутации четырехполюсник находился под воздействием напряжения
. До коммутации четырехполюсник находился под воздействием напряжения  .
.
1. Составляем дифференциальное уравнение цепи. Четырехполюсник описывается следующими уравнениями:
 , (1.49)
, (1.49)
 , (1.50)
, (1.50)
 , (1.51)
, (1.51)
 . (1.52)
. (1.52)
Подставим (1.52) в (1.49)
 . (1.53)
. (1.53)
Неизвестный ток  найдем из уравнений (1.50) и (1.51)
найдем из уравнений (1.50) и (1.51)
 . (1.54)
. (1.54)
С учетом (1.54) уравнение (1.53) примет следующий вид:
 .
.
Дифференцируя два раза, получим
 . (1.55)
. (1.55)
Подставляя в (1.55) исходные данные, получим искомое дифференциальное уравнение типа "вход-выход"
 .
.
2. Решаем однородное уравнение (определяем свободную составляющую)
 .
.
Составим характеристическое уравнение
 .
.
Корни  кратные, кратность
кратные, кратность  . Общее решение будет иметь вид
. Общее решение будет иметь вид
 . (1.56)
. (1.56)
3. Определяем частное решение  неоднородного уравнения (принужденную составляющую)
неоднородного уравнения (принужденную составляющую)
 . (1.57)
. (1.57)
Правая часть (1.57) равна  . В соответствии с (1.36) частное решение
. В соответствии с (1.36) частное решение
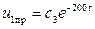 .
.
Подставив его в (1.57), получим уравнение для определения 
 .
.
Откуда следует, что  . Тогда
. Тогда
 . (1.58)
. (1.58)
4. Составим систему уравнений для определения произвольных постоянных  и
и  . Согласно (1.26), (1.56) и (1.58)
. Согласно (1.26), (1.56) и (1.58)
 .
.
Поскольку искомых постоянных только две, то система (1.48) примет следующий вид:
 , (1.59)
, (1.59)
 . (1.60)
. (1.60)
5. Определим переменные состояния. Для этого рассматриваем схему до коммутации. Учитывая, что до коммутации на входе четырехполюсника действовало постоянное напряжение и процесс носил установившийся характер, получаем, что ток в цепи
 . (1.61)
. (1.61)
Тогда из (1.49) с учетом того, что 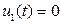 , следует:
, следует:
 В, (1.62)
В, (1.62)
а из (1.61)
 . (1.63)
. (1.63)
6. Определим начальные условия  и
и  . Для этого воспользуемся уравнением (1.49). Учитывая (1.50), (1.62) и (1.63), получаем
. Для этого воспользуемся уравнением (1.49). Учитывая (1.50), (1.62) и (1.63), получаем
 . (1.64)
. (1.64)
Чтобы найти  , продифференцируем (1.49)
, продифференцируем (1.49)
 . (1.65)
. (1.65)
Из (1.52) следует, что  , а из (1.50) и (1.51)
, а из (1.50) и (1.51)  . Поэтому согласно (1.65)
. Поэтому согласно (1.65)

 . (1.66)
. (1.66)
Решая совместно (1.59), (1.60), (1.64) и (1.66), получим
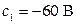 ,
,  .
.
График изменения сигнала на выходе четырехполюсника  представлен на рис. 1.15.
представлен на рис. 1.15.






