Тема2. Загальна теорія систем лінійних рівнянь
САМОСТІЙНА РОБОТА№2
Матричний метод розв’язування систем лінійних рівнянь
Розглянемо систему n лінійних рівнянь з n невідомими:
(1)
Позначимо через А- матрицю, складену із коефіцієнтів при невідомих (так звану основну матрицю системи); X- матрицю-стовпець із невідомих;
B- матрицю-стовпець із вільних членів, тобто 
Тоді систему рівнянь(1) можна переписати у вигляді матричного рівняння: 
Його розв’язок 
називається матричним розв’язком системи лінійних рівнянь з n невідомими.
Знаходження матричного розв’зку називається матричним способом розв’зування систем лінійних рівнянь.
Приклад. Записати і розв’язати в матричній формі систему рівнянь 
Розв’язок. Позначимо через 
Система лінійних рівнянь запишеться у матричній формі
Матричний розв’язок системи буде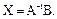 
Для знаходження оберненої матриці 
обчислимо визначник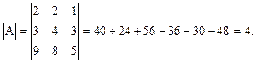 
Оскільки 
то для матриці 
існує обернена 
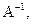а значить, можна знайти єдиний розв’язок вихідної системи.
Знаходимо алгебраїчні доповнення: 
, 
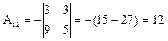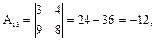
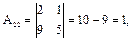
Отже, 
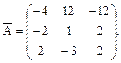Транспонуємо 
тоді 
Обернена матриця має вигляд: 
Перевіряємо:
Обернену матрицю знайдено правильно.
Знаходимо розв’язок заданої системи:
Розв’язок системи лінійних рівнянь: 
Метод Гауса розв’язування систем лінійних рівнянь
Метод Гауса (метод послідовного виключення невідомих) ґрунтується на елементарних перетвореннях системи лінійних алгебраїчних рівнянь, до яких належать:
1. переставляння двох рівнянь місцями;
2. множення обох частин одного з рівнянь системи на одне й те саме число, відмінне від нуля;
3. додавання до обох частин якого – небудь рівняння відповідних частин іншого рівняння, помножених на довільне число;
4. вилучення із системи рівняння, що є тотожністю.
Загальна ідея методу Гауса полягає в тому, що з допомогою елементарних перетворень (при виключенні невідомого 
з усіх рівнянь, починаючи з другого, 
- з усіх рівнянь, починаючи з третього і т.д.) система зводиться до трикутного вигляду:
З одержаної системи послідовно, починаючи з останньої за номером невідомої, рухаючись знизу вгору, знаходять всі інші невідомі.
Часто на практиці замість перетворень над системою виконують відповідні перетворення над розширеною матрицею системи.
Алгоритм методу Гауса:
1. скласти розширену матрицю системи;
2. зробити так, щоб коефіцієнт 
. Для цього можна поміняти
рядки місцями, або поділити перший рядок на 
;
3. в першому стовпці під коефіцієнтом 1 зробити всі нулі. Для цього помножити перший рядок послідовно на 
і додати відповідно до другого, третього,..., m-го рядків;
4. зробити так, щоб коефіцієнт 
, а під ним були нулі;
5. описані дії повторити для всіх діагональних елементів (з однаковими індексами);
6. знайти ранги основної і розширеної матриці системи.
7. за останньою матрицею скласти систему лінійних рівнянь та дослідити її:
а) якщо ранги основної і розширеної матриці не рівні, то система розв’язків не має;
b) якщо ранги основної і розширеної матриці рівні та ранг
системи дорівнює кількості невідомих, то система має єдиний розв’язок.
Його шукають так: з одержаної системи послідовно, починаючи з останньої за номером невідомої, рухаючись знизу вгору, знаходять всі інші невідомі.
с) якщо ранги співпадають, але ранг системи s менший, ніж кількість невідомих n, то ця система невизначена. Розв’язки її шукають так: перші s невідомих 
які називаються базисними визначають через інші невідомі 
..., 
які називаються вільними.
- загальний розв'язок системи.
Якщо замість 
підставити конкретні числові значення, то отримаємо частинний розв'язок системи.
Зокрема, якщо 
, то одержимо розв'язок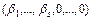 
, який називають базисним.
Приклад 2. Розв'язати методом Гауса систему лінійних рівнянь
Розв’язання.
1) Виконуємо перетворення над розширеною матрицею системи:
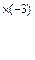
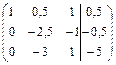: (-2,5) 
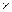3 
Оскільки ранги основної і розширеної матриці співпадають (r =3) і ранг системи дорівнює кількості невідомих, то система має один розв'язок.
2) За останньою матрицею складаємо систему рівнянь.
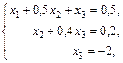
(2; 1; -2) - розв’язок системи.
Відповідь. (2; 1; -2).
Приклад 3. Розв'язати методом Гауса систему лінійних рівнянь
Розв’язання.
1). Виконуємо перетворення над розширеною матрицею системи:
Ранги матриць співпадають (r =2), значить система сумісна.
Оскільки ранг менше числа невідомих (2<4), то система невизначена.
2) За останньою матрицею складаємо систему рівнянь.
,
, 
- загальний розв’язок системи.
Відповідь. (
, 
, 
.
