2. Властивості визначників.
3. Обернені матриці, їх обчислення.
Методичні рекомендації
Ранг матриці.
Розглянемо прямокутну матрицю А розміру m 
n: A= 
Рангом матриці називається найвищий порядок мінора, що не дорівнює нулю.
Ціле число r >0 є рангом матриці А, якщо серед її мінорів r-го порядку є принаймні один, відмінний від нуля, а всі мінори, порядок яких більший, ніж r дорівнюють нулю.
Властивості рангу матриці:
1. Ранг матриці А порядку чисел m n не перевищує меншого з чисел m і n, тобто r 
2. r 
= 0 тоді і тільки тоді, A- нульова матриця
3. Ранг квадратної матриці А n-го порядку дорівнює n тоді і тільки тоді, коли матриця А невиражена, тобто її визначник не дорівнює нулю.
Методи обчислення рангу матриці:
1. Метод окантування (за означенням).
2. Метод, який полягає в застосуванні елементарних перетворень матриці, до яких належать:
a) вилучення нульового рядка (стовпця);
b) множення всіх елементів деякого рядка (стовпця) матриці на число, відмінне від нуля;
c) зміна порядку рядків (стовпців);
d) додавання до кожного елемента деякого рядка (стовпця) відповідних елементів іншого рядка (стовпця), помножених на будь-яке число;
e) транспортування матриці.
За допомогою елементарних перетворень матрицю можна звести до діагонального вигляду. Ранг такої матриці дорівнює кількості діагональних елементів, які не дорівнюють нулю.
Алгоритм обчислення рангу матриці. 
1) Робимо так, щоб елемент 
;
2) Всі елементи 1-го стовпця, що знаходяться під 
робимо рівними нулю;
3) Якщо в результаті перетворень отримали рядок чи стовпець, що містить всі нулі, то його вилучаємо;
4) Повторюємо дії пунктів 1-3 для кожного діагонального елемента (з однаковими індексами), доки не зведемо матрицю до діагонального вигляду.
Приклад. Обчислити ранг матриці A= 
Розв’язання.
1) Поміняємо 1-й і 2-й рядок місцями для того, щоб елемент ;
2) Щоб отримати в 1-му стовпці всі решта нулі, 1-й рядок помножимо на –1 і додамо до 3-го рядка; 1-й рядок помножимо на –2 і додамо до 4-го рядка;
3) Елемент 
. Щоб отримати нулі, 2-й рядок додамо до 3-го рядка; 2-й рядок помножимо на 3 і додамо до 4-го рядка;
4) Вилучимо нульові рядки.
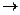
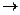
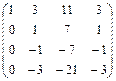
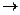
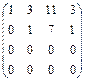
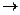
Ранг матриці r 
Cистема m лінійних рівнянь з n невідомими.
Розглянемо систему m лінійних рівнянь з n невідомими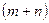 
Теорема 1. ( Кронекера-Капеллі) Для того, щоб система m лінійних рівнянь з n невідомими була сумісною, необхідно і досить, щоб ранги її основної та розширеної матриці були рівні.
Теорема 2. ( умова визначеності системи). Якщо система m лінійних рівнянь з n невідомими сумісна і ранг її основної матриці дорівнює r, то при r =n ця система визначена, а при r <n – невизначена.
Якщо система m лінійних рівнянь з n невідомими зведена до трикутного вигляду і число рівнянь такої системи S менше, ніж число невідомих n, тобто S < n, то розв’язки шукаємо так. Перші S невідомих 
які називають базисними, визначають через інші невідомі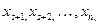 
які називають вільними. Таким чином, стримують загальний розв’зок системи.
Властивості визначників
1. Якщо всі елементи деякого рядка чи стовпця визначника дорівнюють 0, то і сам визначник дорівнює 0.
Це випливає з того, що співмножником у кожному з доданків цих формул (1), (2) є один елемент з кожного рядка і стовпця.
Приклад 1. 1 2 3
4 5 6 = 0
0 0 0
2. Якщо у визначнику поміняти місцями два сусідні рядки чи стовпці, то знаки таких визначників будуть протилежними, а їхні абсолютні величини рівними.
Приклад 2. 1 2 3 0 4 2
0 4 2 = 4 1 2 3 = -4
-1 2 0 -1 2 3
3. Визначник з двома однаковими рядками чи стовпцями дорівнює 0.
1 2 3
1 2 3 = 0 –6 + 6 + 6 - 6 = 0
-1 2 0
4. При транспонуванні визначника його значення не змінюється.
1 2 3 1 0 –1
0 4 2 = 4 2 4 2 = - 4 + 12 – 4 = 4
-1 2 0 3 2 0
5. Якщо всі елементи будь-якого рядка мають спільний множник, то його можна винести за знак визначника.
8 6 2 4 3 1 2 1 1
6 18 3 = 2·3·5 · 2 6 1 = 30·2·3 ·1 2 1 = 180(10– 6) = 720
10 15 10 2 3 2 1 1 2
6. Якщо у визначнику елементи одного рядка пропорційні до відповідних елементів іншого рядка, то визначник дорівнює 0.
Приклад. 4 2 2 2 1 1
2 1 1 = 2· 2 1 1 = 2·0 = 0
-1 2 0 -1 2 0
7. Значення визначників не зміниться, якщо до будь-якого рядка додати інший, помножений на довільне число чи лінійну комбінацію інших рядків.
1 2 3 1 2 3 1 2 3
0 4 2 = 0 4 2 = 0 4 2 = 4
-1 2 0 0 4 3 0 0 1
Обернена матриця
Матриця А-1 називається оберненою до матриці А, якщо виконуються рівності: АА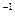 
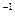= А А=Е.
Якщо визначник матриці А не дорівнює нулю, то така матриця називається неособливою (невиродженою).
Теорема. Для того, щоб матриця мала обернену необхідно і досить, щоб вона була невиродженою.
Алгоритм знаходження оберненої матриці
для заданої квадратної матриці А=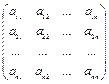 
.
1. Знайти визначник матриці 
;
2. Знайти алгебраїчні доповнення елементів матриці А;
3. Скласти матрицю з алгебраїчних доповнень елементів матриці А;
4. Транспонувати матрицю з алгебраїчних доповнень; ця матриця
називається приєднаною (або союзною) і позначається 
;
5. Поділити приєднану матрицю на визначник даної матриці.
Отже, 
— матриця, обернена до матриці А.
Приклад 1. Знайти матрицю, обернену до матриці 
.
Розв’язання.
1) Знаходимо визначник матриці : 
= 
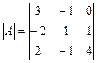Оскільки 
, то обернена матриця існує.
2) Знаходимо алгебраїчні доповнення:
, 
,
, 
,
, 
,
, 
, 
.
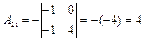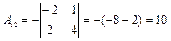3) Таким чином, 
.
4) Транспортуємо матрицю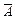 
і знаходимо 
.
5) Отже, обернена матриця 
.
Перевіряємо: 
= 
.
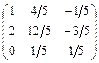Приклад 2. Знайти обернену матрицю для матриці 
Розв’язання.
1) Обчислимо визначник цієї матриці:
.
Оскільки 
, тобто матриця вироджена, то оберненої для неї не існує.
Тести для самоперевірки:
1. Матрицею розміру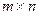 
називають
а) прямокутну таблицю чисел, яка містить 
рядків і 
стовпців;
б) прямокутна таблиця, складена з цілих чисел;
в) прямокутну таблицю чисел, яка містить рядків і стовпців;
г) прямокутну таблицю чисел, яка містить рядків і стовпців.
2. Квадратна матриця -
а) це матриця, в якій число рядків дорівнює числу стовпців;
б) це матриця, всі елементи якої дорівнюють одиниці;
в) це матриця в якій m рядків і n стовпців;
г) інша відповідь.
3. Квадратна матриця називається діагональною, якщо
а) всі елементи головної діагоналі дорівнюють нулю,
б) всі елементи, розміщені поза головною діагоналлю, нулі;
в) матриця складається з одного стовпця;
г) інша відповідь.
4. При множенні двох матриць
а)рядки множать на стовпці;
б) стовпці на рядки;
в) рядки на рядки;
г) стовпці на стовпці.
5. Одиничною матрицею називається
а) діагональна матриця, всі елементи головної діагоналі якої
дорівнюють одиниці,
б) матриця, всі елементи якої, що розміщені поза головною діагоналлю, дорівнюють одиниці;
в) матриця, що складається з одного стовпця;
г) інша відповідь.
6. Нульовою називають матрицю:
a) всі елементи якої, крім діагональних, дорівнюють нулю;
б) всі елементи якої дорівнюють нулю;
в) в якій число рядків дорівнює числу стовпців;
г) в якій елементи розміщені під головною діагоналлю дорівнюють нулю.
7.Множити можна тільки ті матриці, в яких
a) число стовпців першої дорівнює числу рядків другої;
б) число рядків першої дорівнює числу стовпців другої;
в) однакові розміри;
г) інша відповідь.
8.Різницею матриць 
і 
називається матриця, кожний елемент якої 
дорівнює:
а) різниці елементів і -го рядка матриці А та відповідних елементів j -го стовпця матриці В;
б) різниці відповідних елементів матриць А і В;
в) різниці добутків елементів і -го рядка матриці А на відповідні елементи j -го стовпця матриці В;
г) інша відповідь.
9.Рангом матриці називається
а) кількість рядків матриці;
б) найвищий порядок мінора, що дорівнює нулю;
в) найвищий порядок мінора, що не дорівнює нулю;
г) інша відповідь.
