Ця методика побудови картин поля носить нестрогий, а скоріше мнемонічний характер і будується на таких відомих положеннях:
1) у хвиль електричного типу магнітне поле розташоване тільки у поперечній площині; ці хвилі мають повздовжну складову 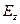 , орієнтовану вздовж хвилеводу;
, орієнтовану вздовж хвилеводу;
2) у хвиль магнітного типу електричне поле розташоване тільки у поперечній площині; ці хвилі мають повздовжну складову 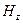 , орієнтовану вздовж хвилеводу;
, орієнтовану вздовж хвилеводу;
3) біля поверхні ідеального металу не існує тангенціальна складова електричного поля; електричні силові лінії є перпендикулярними (нормальними) до поверхні металу;
4) магнітні силові лінії є замкнутими і підходять тангенціально до металу;
5) магнітні та електричні силові лінії у будь-якій точці поля є взаємно – перпендикулярними;
6) індекс m у типі хвилі показує кількість напівхвиль, що розміщуються між стінками хвилеводу у напрямку осі ОХ;
7) індекс n у типі хвилі показує кількість напівхвиль, що розміщуються між стінками хвилеводу у напрямку осі ОY.
Користуючись цими положеннями побудуємо картину поля хвилі  у прямокутному хвилеводі. Оскільки магнітні хвилі мають лише поперечні складові електричного поля, тобто вони у поперечному перетині хвилеводу зображаються у натуральну величину, слід починати побудову саме з цієї проекції.
у прямокутному хвилеводі. Оскільки магнітні хвилі мають лише поперечні складові електричного поля, тобто вони у поперечному перетині хвилеводу зображаються у натуральну величину, слід починати побудову саме з цієї проекції.
У хвилі  є лише одна електрична складова
є лише одна електрична складова  , яка вздовж сторони а утворює одну напівхвилю, залишаючись перпендикулярною до верхньої і нижньої стінок хвилеводу. Згідно з граничними умовами, вектор
, яка вздовж сторони а утворює одну напівхвилю, залишаючись перпендикулярною до верхньої і нижньої стінок хвилеводу. Згідно з граничними умовами, вектор  має дорівнювати нулю при
має дорівнювати нулю при  та
та  , а, отже, буде мати максимальне значення посередині при
, а, отже, буде мати максимальне значення посередині при  (рис.1.9.1).
(рис.1.9.1).

Рисунок 1.9.1
Вздовж напрямку OY (вздовж сторони b) вектор  залишається незмінним. У цьому ж перетині хвилеводу будемо бачити і складову поля
залишається незмінним. У цьому ж перетині хвилеводу будемо бачити і складову поля 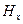 , яка має бути перпендикулярною до
, яка має бути перпендикулярною до  (горизонтальною). Магнітні складові поля будемо зображати штриховими лініями. Оскільки досліджувальна хвиля є магнітною, вона має ще й повздовжню складову
(горизонтальною). Магнітні складові поля будемо зображати штриховими лініями. Оскільки досліджувальна хвиля є магнітною, вона має ще й повздовжню складову 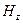 , у яку плавно має перейти поперечна складова
, у яку плавно має перейти поперечна складова 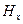 і утворити разом замкнуту лінію. Цей перехід з утворенням замкнутої лінії магнітного поля зображено на рис. 1.8.4б та рис. 1.9.1б.
і утворити разом замкнуту лінію. Цей перехід з утворенням замкнутої лінії магнітного поля зображено на рис. 1.8.4б та рис. 1.9.1б.

Рисунок 1.9.2
На рис. 1.9.2 показані картини полів декількох хвиль з малими значеннями індексів m та n:  . Нагадаємо, що починати побудову картини поля будь-якої хвилі слід з поперечного перетину і для силових ліній тих складових, які є лише поперечними. Тобто для
. Нагадаємо, що починати побудову картини поля будь-якої хвилі слід з поперечного перетину і для силових ліній тих складових, які є лише поперечними. Тобто для  хвиль починають з вектора
хвиль починають з вектора  , для
, для  - з вектора
- з вектора  .
.

Рисунок 1.9.3
При переході, наприклад, від хвилі  до хвилі
до хвилі  картина поля у напрямку х подвоюється (порівняйте рис 1.9.1а та 1.9.2а). аналогічне подвоєння у напрямку х (подвоївся перший індекс) бачимо з порівняння рис 1.9.2б з 1.9.3а, рис. 1.9.2в з 1.9.3б.
картина поля у напрямку х подвоюється (порівняйте рис 1.9.1а та 1.9.2а). аналогічне подвоєння у напрямку х (подвоївся перший індекс) бачимо з порівняння рис 1.9.2б з 1.9.3а, рис. 1.9.2в з 1.9.3б.
При зростанні удвічі других індексів (перехід до хвиль  та
та  ) подвоїлись би картинки у напрямку у, зображені на рис. 1.9.3.
) подвоїлись би картинки у напрямку у, зображені на рис. 1.9.3.
Круглий хвилевід
Круглий (циліндричний) хвилевід, у якому можуть поширюватись хвилі  та
та  типів, представляє собою металеву круглу трубу (циліндр). При аналізі круглих циліндричних хвилеводів доцільно використовувати циліндричну систему координат, розташувавши їх так, як показано на рис. 1.10.1.
типів, представляє собою металеву круглу трубу (циліндр). При аналізі круглих циліндричних хвилеводів доцільно використовувати циліндричну систему координат, розташувавши їх так, як показано на рис. 1.10.1.

Рисунок 1.10.1
Хвиля електричного типу
Запишемо рівняння Гельмгольця для хвиль електричного типу циліндричної системи координат:
 (1.10.1)
(1.10.1)
Розв’яжемо рівняння (1.10.1) методом розділення змінних за Фур’є.
Покладемо, що
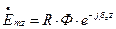 (1.10.2)
(1.10.2)
де  .
.
Помножимо (1.10.1) на  , підставимо у нього (1.10.2) і розділимо отриманий результат на
, підставимо у нього (1.10.2) і розділимо отриманий результат на  . Тоді отримаємо:
. Тоді отримаємо:
 .
.
Розділимо останнє рівняння на  і отримаємо:
і отримаємо:
.  . (1.10.3)
. (1.10.3)
Три перших доданки у виразі (1.10.3) є функціями лише координати  (у дужках), а четвертий – функцією координати
(у дужках), а четвертий – функцією координати 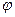 . Оскільки
. Оскільки  є незалежними змінними, то у останньому виразі маємо суму двох взаємно – незалежних функцій, яка дорівнює нулю. Це можливо, коли кожна з цих функцій буде дорівнювати одному і тому самому постійному числу, але взятим з протилежними знаками:
є незалежними змінними, то у останньому виразі маємо суму двох взаємно – незалежних функцій, яка дорівнює нулю. Це можливо, коли кожна з цих функцій буде дорівнювати одному і тому самому постійному числу, але взятим з протилежними знаками:
 ,
,  .
.
Якщо перше з цих рівнянь помножити на 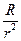 , отримаємо:
, отримаємо:
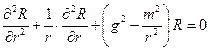 . (1.10.4)
. (1.10.4)
Помноживши друге на  , матимемо:
, матимемо:
 . (1.10.5)
. (1.10.5)
Розв’язком рівняння (1.10.5), як відомо з математики, є функція:

де  ,
,  .
.
Оскільки при дослідженні поширення хвиль в круглому хвилеводі вибір початку відліку 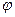 є довільним, покладемо
є довільним, покладемо  і тоді:
і тоді:
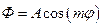 . (1.10.6)
. (1.10.6)
Число  може приймати значення 0, 1, 2, 3,…
може приймати значення 0, 1, 2, 3,…
Рівняння (1.10.4) досліджувалось німецьким математиком Бесселем. Показано, що його розв’язком є функція:
 , (1.10.7)
, (1.10.7)
де 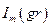 - функція Бесселя 1-го роду m – го порядку,
- функція Бесселя 1-го роду m – го порядку,  - функція Бесселя 2-го рода m – го порядку (останню ще називають функцією Неймана m – го порядку). Порядок цих функцій визначає той самий коефіцієнт m, який входить у вираз (1.10.6). Число m визначає кількість варіацій поля вздовж координатної лінії
- функція Бесселя 2-го рода m – го порядку (останню ще називають функцією Неймана m – го порядку). Порядок цих функцій визначає той самий коефіцієнт m, який входить у вираз (1.10.6). Число m визначає кількість варіацій поля вздовж координатної лінії 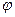 циліндричної системи координат, у якій розглядається спрямовуюча система (хвилевід).
циліндричної системи координат, у якій розглядається спрямовуюча система (хвилевід).

Рисунок 1.10.2
На рис 1.10.2 показані графіки функцій 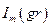 та
та  при
при  та
та  . Координати точок перетину цих кривих з віссю абсцисс є коренями відповідних функцій.
. Координати точок перетину цих кривих з віссю абсцисс є коренями відповідних функцій.
Як бачимо, при 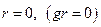 , в усіх точках хвилеводу, які лежать на осі OZ,
, в усіх точках хвилеводу, які лежать на осі OZ,  . Тобто функція R, а отже і
. Тобто функція R, а отже і  є нескінченно – великими, що суперечить здоровому глузду, бо з точки зору фізики поле може мати лише скінченні значення його складових. Таким чином, при дослідженні процесів у круглих хвилеводах у розв’язку (1.10.7) маємо покласти
є нескінченно – великими, що суперечить здоровому глузду, бо з точки зору фізики поле може мати лише скінченні значення його складових. Таким чином, при дослідженні процесів у круглих хвилеводах у розв’язку (1.10.7) маємо покласти  . Тоді його вигляд буде таким:
. Тоді його вигляд буде таким:
 (1.10.8)
(1.10.8)
Підставивши (1.10.6) та (1.10.8) у вираз (1.10.2), отримаємо:
 (1.10.9)
(1.10.9)
 є дотичною (тангенціальною) до стінок хвилеводу і при
є дотичною (тангенціальною) до стінок хвилеводу і при 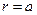 дорівнює нулю, тобто при
дорівнює нулю, тобто при 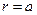
 , звідки
, звідки
 (1.10.10)
(1.10.10)
та  (1.10.11)
(1.10.11)
де  - корінь функції Бесселя першого роду m – го порядку за номером n. З виразу (1.10.11) маємо:
- корінь функції Бесселя першого роду m – го порядку за номером n. З виразу (1.10.11) маємо:
 (1.10.12)
(1.10.12)
Значення кореня можна визначити з графіків для функцій 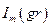 або з таблиці (див. довідник з вищої математики), фрагмент якої показано таблицьою 1.10.1.
або з таблиці (див. довідник з вищої математики), фрагмент якої показано таблицьою 1.10.1.
Таблиця 1.10.1
| n | m | ||
| 2,405 | 3,832 | 5,135 | |
| 5,520 | 7,016 | 8,417 | |
| 8,654 | 10,174 | 11,620 | |
| .. | … | … | … |
З урахуванням (1.10.12), вираз (1.10.9) перепишеться так:
 (1.10.13)
(1.10.13)
Підставивши (1.10.13) у вирази (1.10.11) – (1.10.14) при  (поле електричного типу), отримаємо вирази для складових полів хвиль типів
(поле електричного типу), отримаємо вирази для складових полів хвиль типів  у циліндричному (круглому) хвилеводі:
у циліндричному (круглому) хвилеводі:
 . (1.10.14)
. (1.10.14)
Повздовжнє хвильове число 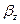 визначається за формулою (1.3.7):
визначається за формулою (1.3.7):
 . (1.10.15)
. (1.10.15)
Згідно (1.3.10) для хвиль типу  у циліндричному хвилеводі:
у циліндричному хвилеводі:
 , (1.10.16)
, (1.10.16)
їх фазова швидкість, виходячи з (1.5.2), дорівнюватиме:
 . (1.10.17)
. (1.10.17)
а хвильовий опір, з урахуванням (1.6.9):

Хвилі магнітного типу
У таких хвилях тангенціальними до стінок хвилеводу будуть складові  , які через
, які через  можна виразити за формулою(1.4.13):
можна виразити за формулою(1.4.13):
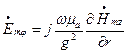 .
.
Вираз для 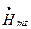 знайдемо, розв’язавши рівняння Гельмгольця:
знайдемо, розв’язавши рівняння Гельмгольця:
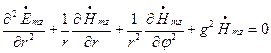 . (1.10.18)
. (1.10.18)
Оскільки це рівняння за конструкцією збігається з рівнянням (1.10.1), то і розв’язок рівняння (1.10.18) за конструкцією збігається з виразом (1.10.13):
 . (1.10.19)
. (1.10.19)
Скориставшись тим, що складова  є тангенціальною до циліндричної стінки хвилеводу, то при
є тангенціальною до циліндричної стінки хвилеводу, то при 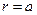 вона дорівнюватиме нулю і
вона дорівнюватиме нулю і
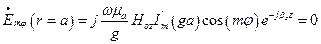 ,
,
звідки  (1.10.20)
(1.10.20)
де  - n – й корінь першої похідної функції Бесселя
- n – й корінь першої похідної функції Бесселя  першого роду m –го порядку. Графіки
першого роду m –го порядку. Графіки  схожі на графіки
схожі на графіки 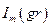 , розглянуті вище. В табл. 1.10.2 наведені значення коренів декількох перших похідних функцій Бесселя
, розглянуті вище. В табл. 1.10.2 наведені значення коренів декількох перших похідних функцій Бесселя  .
.
Таблиця 1.10.2
| n | m | ||
| 3,832 | 1,840 | 3,054 | |
| 7,016 | 5,335 | 6,705 | |
| 10,174 | 8,536 | 9,965 | |
| .. | … | … | … |
З урахуванням (1.10.20) вираз для 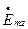 можна переписати так:
можна переписати так:
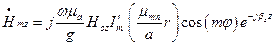 . (1.10.21)
. (1.10.21)
Підставивши (1.10.21) в рівняння (1.4.11) – (1.4.14) при 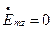 матимемо вирази для складових хвиль типу
матимемо вирази для складових хвиль типу  у круглому циліндричному хвилеводі:
у круглому циліндричному хвилеводі:
 . (1.10.22)
. (1.10.22)
Повздовжнє хвильове число 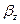 визначається за формулою (1.3.7):
визначається за формулою (1.3.7):
 . (1.10.23)
. (1.10.23)
У відповідності до (1.3.10) для хвиль типу  у циліндричному хвилеводі:
у циліндричному хвилеводі:
 . (1.10.24)
. (1.10.24)
Їх фазова швидкість, виходячи з (1.5.2), дорівнюватиме:
 , (1.10.25)
, (1.10.25)
а хвильовий опір, з урахуванням (1.6.15):
 . (1.10.26)
. (1.10.26)






