1. Үш жәшікте 200 алма бар еді. Бірінші жәшіктегі алмалардың 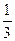 бөлігін, екіншідегінің -
бөлігін, екіншідегінің - 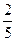 , үшіншідегінің
, үшіншідегінің 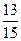 - бөлігін алғанда, барлығы 70 алма алынған. Егер екінші жәшіктегі алмалардың
- бөлігін алғанда, барлығы 70 алма алынған. Егер екінші жәшіктегі алмалардың 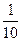 бөлігін, ал үшіншіден
бөлігін, ал үшіншіден 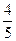 бөлігін алғанда, барлығы қанша алма алынған болар еді?
бөлігін алғанда, барлығы қанша алма алынған болар еді?
Шешуі. Есептің шартынан бірінші жәшіктегі алмалар санының 3-ке, екінші жәшіктегі - 10-ға, ал үшіншідегі 15-ке бөлінетіндігін көру қиын емес. Егер бірінші жәшіктегі алмалар санын 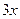 , екіншідегі
, екіншідегі 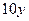 , үшіншідегі
, үшіншідегі 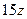 деп белгілесек, онда
деп белгілесек, онда
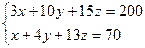
Екінші теңдеуді 3-ке көбейтіп, одан бірінші теңдеудін сәйкес мүшелерін шегерсек:
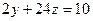 немесе
немесе  .
.
Сонымен, ізделінді алмалар саны 5.
2. Екі жұмысшы бірігіп 1000-нан аз деталь дайындауға тапсырма алды. Бірінші жұмысшы бірінші, екінші, үшінші күндері өз тапсырмасының 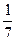 ,
, 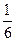 және
және 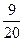 бөліктерін, ал екінші жұмысшы сол күндері сәйкесінше өз тапсырмасының
бөліктерін, ал екінші жұмысшы сол күндері сәйкесінше өз тапсырмасының 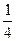 ,
, 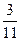 және
және 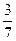 бөліктерін орындады. Әр жұмысшы үшінші күні қанша детальдан дайындады?
бөліктерін орындады. Әр жұмысшы үшінші күні қанша детальдан дайындады?
Шешуі. Әркүні дайындалатын детальдар саны бүтін болғандықтан, бірінші жұмысшының жасаған детальдарының саны 7, 6, 20 сандарына, яғни 420 санына, ал екіншінің жұмысшының жасаған детальдарының саны 4, 11, 7 сандарына, яғни 308 санына қалдықсыз бөлінуі керек. Барлық детальдар саны 1000-нан кіші болғандықтан, бірінші жұмысшының жасаған детальдарының саны 420 (840 емес), ал екінші жұмысшының жасаған детальдарының саны 308 (616 немесе 924 емес). Демек, үшінші күні бірінші жұмысшы 189, ал екінші жұмысшы 132 деталь дайындаған.
3. Дәл квадрат болатын төрт орынды санның бірінші цифры екіншісіне, ал үшіншісі төртіншісіне тең. Осы санды табыңыз.
Шешуі. Ізделінді сан 11-ге бөлінеді. Содықтан, 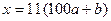 болсын. 11 жай сан және
болсын. 11 жай сан және 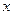 дәл квадрат болғандықтан,
дәл квадрат болғандықтан,  саны да 11-ге бөлінеді.
саны да 11-ге бөлінеді. 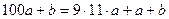 тепе-теңдігінен
тепе-теңдігінен  болуы керектігін көреміз. Қосындысы 11 болатын цифрлар ішінен есеп шартын қанағаттандыратындары
болуы керектігін көреміз. Қосындысы 11 болатын цифрлар ішінен есеп шартын қанағаттандыратындары 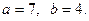 Демек, ізделінді сан
Демек, ізделінді сан 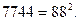
4. 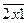 түріндегі үш орынды санды 2011 рет қатар жазғанда пайда болған сан 11 санына бөлінеді. Сонда
түріндегі үш орынды санды 2011 рет қатар жазғанда пайда болған сан 11 санына бөлінеді. Сонда 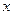 қандай цифр болғаны?
қандай цифр болғаны?
Шешуі.  түріндегі сан әр уақытта 11-ге бөлінеді. Шынында да,
түріндегі сан әр уақытта 11-ге бөлінеді. Шынында да,
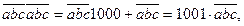
ал 1001 саны 11-ге бөлінеді. 2010 жұп сан болғандықтан, 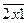 санын 2010 рет қайталап жазғанда пайда болған сан 11-ге бөлінеді. Демек, 2011 рет қайталап жазғанда пайда болған сан 11-ге бөлінуі үшін
санын 2010 рет қайталап жазғанда пайда болған сан 11-ге бөлінеді. Демек, 2011 рет қайталап жазғанда пайда болған сан 11-ге бөлінуі үшін 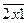 санының 11-ге бөлінуі қажет.
санының 11-ге бөлінуі қажет. 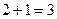 болғандықтан, 11-ге бөлінгіштіктің белгісі бойынша,
болғандықтан, 11-ге бөлінгіштіктің белгісі бойынша,  .
.
5. Үш орынды  санын 7-ге көбейткенде натурал саннын кубы алынды.
санын 7-ге көбейткенде натурал саннын кубы алынды.  санын анықтаңыз.
санын анықтаңыз.
Шешуі. 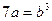 болсын. Онда
болсын. Онда 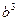 саны 7-ге бөлінеді, яғни
саны 7-ге бөлінеді, яғни  да 7-ге бөлінеді.
да 7-ге бөлінеді. 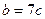 десек, онда
десек, онда 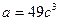 болады. Яғни,
болады. Яғни,  саны 49-ға бөлінеді және бөліндісі натурал санның кубы болады.
саны 49-ға бөлінеді және бөліндісі натурал санның кубы болады.  саны үш орынды болғандықтан
саны үш орынды болғандықтан 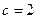 . Демек,
. Демек, 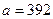 .
.
6. 82-ге бөлінетін 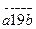 түріндегі төрт орынды сандарды табыңыз.
түріндегі төрт орынды сандарды табыңыз.
Шешуі. Ізделінді сан 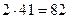 -ге бөлінетін болғандықтан, оның соңғы цифры жұп сан, яғни
-ге бөлінетін болғандықтан, оның соңғы цифры жұп сан, яғни 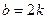 , мұнағы
, мұнағы 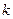 0, 1, 2, 3, 4 мәндерін қабылдай алады. Сонымен,
0, 1, 2, 3, 4 мәндерін қабылдай алады. Сонымен, 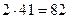 -ге бөлінетін
-ге бөлінетін 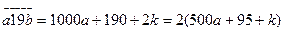 санын табуымыз крек. Ол үшін 41-ге бөлінетін
санын табуымыз крек. Ол үшін 41-ге бөлінетін 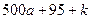 санын анықтасақ жеткілікті.
санын анықтасақ жеткілікті. 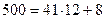 және
және 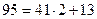 болғандықтан,
болғандықтан, 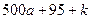 санын келесідей өрнектей аламыз:
санын келесідей өрнектей аламыз: 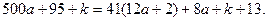 Енді
Енді 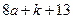 саны 41-ге бөлінетіндей
саны 41-ге бөлінетіндей  мен
мен 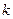 -ны анықтаумыз керек.
-ны анықтаумыз керек.  -ның қабылдайтын мәндері 1 мен 9 аралығындағы тоғыз цифрлар болғандықтан,
-ның қабылдайтын мәндері 1 мен 9 аралығындағы тоғыз цифрлар болғандықтан, 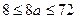 . Ал
. Ал 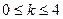 болғандықтан,
болғандықтан, 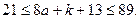 Осы аралықтағы 41 және 82 сандары 41-ге бөлінеді.
Осы аралықтағы 41 және 82 сандары 41-ге бөлінеді.
а) 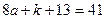 болса, онда
болса, онда 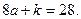 Ал
Ал 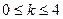 болғандықтан
болғандықтан 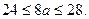 Демек,
Демек, 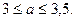
 цифр болғандықтан
цифр болғандықтан 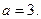 Сонымен,
Сонымен, 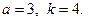
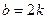 болғандықтан
болғандықтан 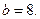 Ізделінді сан 3198.
Ізделінді сан 3198.
ә) 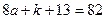 болса, онда
болса, онда 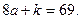
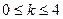 болғандықтан
болғандықтан 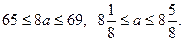
 -ның теңсіздікті қанағаттандыратындай мәні жоқ.
-ның теңсіздікті қанағаттандыратындай мәні жоқ.






