Натурал (оң бүтін) сандар жиынының анықтамасынан салдар ретінде математикалық дәлелдеулердің маңызды әдістерінің бірі-математикалық индукция әдісі шығады.
Әрбір натурал 
үшін 
тұжырымы айтылған болсын. Әрине, кейбір -дер үшін орындалып, кейбір -дер үшін орындалмауы да мүмкін. Бірақ, егер
1) 
орындалса,
2) әрбір натурал үшін орындалғанда 
де орындалса, онда тұжырымы кез келген натурал үшін орындалады.
Расында да, орындалатын 
сандарынан құрылған жиынды 
әрпімен белгілесек, онда 
және 
шарттары орындалады. Сондықтан, натурал сандардың анықтамасы бойынша натурал сандар жиынының дәл өзі болады, яғни тұжырымы кез келген үшін орындалады (әрбір 
үшін 
орындалады ғой!).
Барлық натурал сандар туралы теореманы дәлелдегенде, яғни тұжырымы әрбір натурал саны үшін орындалатынын дәлелдеу үшін, әрқашанда келесі, математикалық индукция әдісі деп аталатын, әдісті қолдану керек:
1) және 2) шарттарының орындалатынын тексеру қажет.
Математикалық индукция әдісін қолдану мысалы ретінде кез келген оң бүтін саны мен кез келген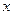 
нақты саны үшін
теңдігі орындалатынын дәлелдейік.
Бұл – Ньютон биномының формуласы – (бином- қос мүшелік), 
дәрежесінің коэффициенті биномдық коэффициент деп аталады да, 
немесе 
символдарымен белгіленеді.
Сонымен, 
ал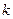 
саны 1, 2,..., сандарының бірі болғанда 
Осы белгілеулерді қолданып, Ньютон биномының формуласын қыскаша былай жазуға болады:
(1) тұжырымын символымен белгілейік.
Әрине, Ньютон биномының формуласын дәлелдеу әрбір оң бүтін саны үшін орындалуын дәлелдеумен пара-пар.
-дің орындалуы айқын, өткені 
болғандықтан,
Сондықтан, жоғарыда айтылған бойынша, әрбір оң бүтін үшін орындалатынын дәлелдеу үшін әрқашан мен бірге 
орындалатынын дәлелдеу жеткілікті.
Сөйтіп, тұжырымы, яғни (1) теңдігі орындалсын. -ді дәлелдеу үшін, әуелі биномдық коэффициенттердің келесі қасиетін атап өтейік.
Яғни,
Енді (2) теңдігін қолданып, тұжырымын былай дәлелдей
аламыз:
(мұнда 
теңдіктері де пайдаланылады).
(1) - формула
түрінде де қолданылады (мұнда 
мен 
- нақты сандар).
(3)-ті дәлелдеу үшін
тепе-теңдігін қолданып, 
болғанда (1) теңдігін пайдалансақ болғаны.
Мектеп оқушылары арасында математиканы кең насихаттау
мақсатында әр деңгейдегі математикалық олимпиадалар жүйелі түрде өткізіліп тұрады. Олимпиадаларды өткізудегі негізгі мақсат оқушылардың математикаға деген қызығушылығын арттыру, олардың бойындағы бейімділіктің ашылып, одан әрі дамуына жәрдем ету екедігі белгілі. Соңғы жылдары әрқилы аймақтық, жекелеген оқу орындары, математикалық журналдар ұйымдастырған олимпиадалар да өткізіліп жүр.
Олимпиадаларда ұсынылатын есептер математика курсының әр алуан тақырыптарын қамтиды. Сондай тақырыптардың бірі сандардың бөлінгіштігі. Ондай есептерді шығару үшін орта мектеп программасындағы теориялық білім, негізінен жеткілікті.
Сандардың 3-ке, 5-ке және 9-ға бөлінгіштік белгілерімектеп курсынан белгілі. Санның 7-ге немесе 13-ке бөлінгіштігін анықтау үшін оның цифрларын оңнан солға қарай үш цифрдан топтастырады. Содан кейін, жұп және тақ орындағы сандардың қосындыларын жеке анықтап, пайда болған қосындылардың айырымын табады. Егер айырым 7-ге немесе 13-ке бөлінсе, онда берілген сан да 7-ге немесе 13-ке бөлінеді.
Мысалы, 52307512901 санының тақ орындағы топтары қосындысы 1208-ге тең 901 және 307 сандарынан, ал жұп орындағы топтары қосындысы 564 болатын 512 және 52 сандарынан тұрады. Осы қосындылардың айырымы 1208-564=644 саны 7-ге бөлінеді. Демек, берілген сан да 7-ге бөлінеді.
Санның бірліктерінен бастап, тақ және жұп орындарда тұрған цифрларынан құралған екі қосындының айырымы 11-ге бөлінсе, онда берілген сан да 11-ге бөлінеді.
Мысалы, 65791 саны 11-ге бөлінеді, өйткені (1+7+6) – (9+5) =0 саны 11-ге бөлінеді.
Сандардың қандай да бір санға бөлінгіштігін дәлелдегенде, кез келген 
оң бүтін саны мен кез келген және нақты сандары үшін орынды, келесі жіктеу формулалары жиі пайдаланылады:
1) Ньютон биномының формуласы
2) 
3) 
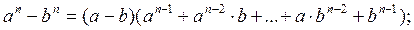
4) 
Енді сандар бөлінгіштігіне қатысты қалыпты емес есептерді қарастырайық.
