Изменениях воздействующего фактора

Лекция 30

1. Динамические свойства э-опривода постоянного и переменного тока с линейной мех-кой хар-кой при различных способах управления. 2. Э-омех-кая постоянная времени и ее физический смысл. 3. Э-омагнитная постоянная времени, исследование ПП-сов с ее учетом.

Объектом исследования будет упрощенная, идеализированная модель привода – рис. 5.1.

Рис. 5.1– Модель э-опривода для исследования динамики

Целью изучения ПП-сов будет определение зависимостей w(t), М(t) и иногда i(t) при известных условиях ПП-са и пар-рах привода.

1. Различные способы управления – это значит ЭД можно сразу на полное напряжение питания подключать, либо ступенчато изменять, либо плавно. Частоту вращения АД можно регулировать путем изменения U₁ и f₁.

Динамические свойства э-опривода – это пуск, реверс, торможение, переход с одной скорости на другую (с одной хар-ки на другую), увеличение или уменьшение нагрузки на валу. ПП-сы могут производиться вхолостую и под нагрузкой. Все (общий курс эопривода Ильинский – 78стр) ПП-сы подчиняются мех-кому уравнению движения

М – М_С = J_∑dω/dt (5.1)

Искомые зависимости w(t) и M(t) должны быть получены путем решения этого уравнения при заданных начальных условиях. Особенности привода отразятся в виде зависимостей M(w) и M_с(w), входящих в уравнение (5.1).

ПП-сы при L = 0 (L – электрические (э-омагнитные) инерционности малы или не

проявляются, т.е. преобладающей инерционностью в приводе является мех-кая

инерционность (J);) и “ быстрых ” изменениях воздействующего фактора.

а) Рассмотрим случая, когда в ПП-се M = const, M_с = const (т.е. ПП вызван изменением U₁).

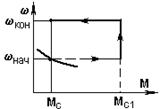
Рис. 5.2 – Мех-кие хар-ки (а) и временные зависимости (б) при М = const и M_c = const

Пусть привод (рис.5.1) работал в точке w _нач, М _нач = М _с (рис.5.2) некоторой хар-ки (она нас не интересует) и в момент времени t = 0 был мгновенно переведен на новую хар-ку, показанную на рис. 5.2,а жирной линией.

Уравнение (5.1) в этом случае – дифференциальное уравнение с разделяющимися переменными и его решение имеет вид:

(М₁ – это М_ЭД)

Постоянную интегрирования С найдем из начального условия – при t = 0, w = w _нач: w _нач = С.

Окончательно будем иметь:

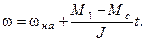(5.2)

Это решение действует на интервале w _нач < w < w _кон, т. к. по условию при w = w _кон функция w(М) терпит излом. На этом интервале М = М₁.

Графики ПП-са приведены на рис.5.2,б. Время ПП-са t _пп можно найти, подставив в (5.2) w = w _кон и решив относительно t:

(5.3)

Этот же результат можно получить, решив (5.1) относительно dt и взяв определенный интеграл:

Рассмотренный простейший случай имеет большое практическое значение, т. к. к нему может быть сведено в целях оценки времени и хар-ра ПП-са большое число конкретных задач.

Оценим время пуска t_п короткозамкнутого АД с известными мех-кой хар-кой, М_с и J (рис.5.3,а). Заменим реальную хар-ку (сплошная линия) приближенной (пунктирная линия) и применив (5.3), получим:

Рис. 5.3 – Мех-кие хар-ки (а) и графики ПП-сов w(t) и M(t) при пуске АД

Зная t_п, можно построить приближенные графики ПП-са (пунктир на рис.5.3,б). Эти графики будут отличаться от действительных (сплошные линии на рис. 5.3,б), однако во многих случаях полученная оценка может быть весьма полезной.

(Н.Ф. ИЛЬИНСКИЙ ОСНОВЫ Э-ОПРИВОДА lek 5; общий курс эопривода Ильинский – 78стр; Elektroprivod – 195стр.). При мгновенном изменении f₁ и U₁ мгновенно устанавливается новая мех-кая хар-ка, а изменение скорости w и момента М в ПП-се происходит согласно этой хар-ке. ПП определяется статической мех-кой хар-кой привода.

б) М_с = const, M линейно зависит от w, b < 0.

Проведем анализ (elektroprivod Онищенко -191стр) э-омех-кой системы, состоящей из двигателя с линейной мех-кой хар-кой и жест­кoгo мех-кого звена. Движение такой э-омех-кой системы определяет­ся уравнением движения э-опривода

М – М_с = J_∑dω/dt (1)

Линейная мех-кая хар-ка описывается ypaвнением

М = β(ω₀ – ω). (2)

Совместное решение (1) и (2) позволяет получить ypaвнение, описывающее ПП-сы двигателя, опреде­ляемые мех-кой инерционностью э-опривода

β(ω₀ – ω) – М_с = J_∑dω/dt → . (3)

2. Из других источников (Н.Ф. ИЛЬИНСКИЙ ОСНОВЫ Э-ОПРИВОДА lek 5) берут модуль величины, стоящей в знаменателе . Величину, стоящую перед производной,

, или так T_M = J_∑/β

называют э-омех-кой постоянной времени.

Для выяснения смысла этой величины рассмотрим условный привод с хар-кой (рис.5.5).

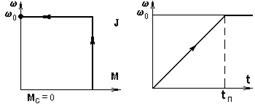
Рис. 5.5 – К определению э-омех-кой постоянной времени Т_м

Определив время разгона такого привода по (5.3)

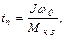
замечаем, что оно выражается так же, как Т _м. Т_м – время, за которое привод разогнался бы вхолостую до w = w₀ под действием момента короткого замыкания.

Мех-кая инерция хар-ризуется э-омех-кой постоянной времени Т _м. Для ДПТ она представляет собой время, в течение которого привод с моментом инерции J разгоняется вхолостую из неподвижного состояния до скорости идеального ХХ при неизменном моменте, равном моменту короткого замыкания.

Величина М_с/β представляет собой падение скорости от нагрузки –­ статическую ошибку Δω_с, а величина (ω₀ – М_с/β) ­– установившееся значение скорости ω_уст после окончания ПП-са, когда М станет равным М_с (рис.8.3,а).

Рис.8.3 – ПП пуска э-опривода:1–механич. и 2 –переходная хар-ка

Используя Т_М получим выражение для переходной хар-ки э-опри­вода (Moskolenko_Elektricheskiy_privod – 110 стр):

.

В рассматриваемом ПП-се как для скорости, так и для момента справедливо одинаковое уравнение вида

, (5.8)

Видно, что в рассматриваемом ПП-се как для скорости, так и для момента справедливо одинаковое уравнение. Решение (5.8) имеет вид

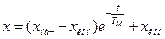, (5.10)

то есть скорость и момент изменяются в ПП-се от начальных до конечных значений по экспоненциальному закону с постоянной времени Т_м (рис. 8.3).

Напомним некоторые важные свойства экспоненты.

1. Касательная в любой точке отсекает на линии установившегося состояния отрезок, равный Т_м.

2. За время t = Т_м изменение величины составляет 0,632 от полного изменения.

3. За время t = 3 Т_м изменение составляет 0,95 от полного. В дальнейшем мы будем считать, что процесс устанавливается за t = 3 Т_м.

Уравнение (5.10) позволяет решать любые задачи, относящиеся к рассматриваемому типу.

ПП-сы, определяемые одной мех-кой инерционностью, суммарным приведенным к валу ЭД моментом инерции J_∑ описываются ДУ первого порядка (5.8). Решением этого уравнения является пере­ходная хар-ка, имеющая вид экспоненты с постоянной времени Т _М (рис.8.3,б):

при ω_нач= 0: (индексы уст ≡ кон)

Ток, момент и скорость двигателя с линейной мех-кой хар-кой в переходных режимах изменяются по экспоненциальному закону.

Рассчитаем ПП мгновенного наброса нагрузки от М_с1 до М_с2 на АД с КЗ котором с мех-кой хар-кой, линейной на рабочем участке (рис. 5.6).

Вычислим Т_м:

 

Определим начальные и конечные значения w и М:

w_нач = w₁, w_кон = w₂;

М_нач = М_с1, М_кон = М_с2

Рис.5.6 – ПП наброса нагрузки

Запишем по (5.10) уравнения ПП-са

ω = (ω₁ – ω₂)e^-t/Tм ₊ ω₂ ;

M = (M_c1 – M_c2)e^-t/Tм ₊ M_c2 ;

и построим графики (рис.5.6).

ПП-сы при L = 0 (L – электрические (электромагнитные) инерционности и “ медленных ”

изменениях воздействующего фактора

К задачам данной группы относят ПП-сы в системе преобразователь – двигатель (П-Д). Фактор, вызывающий ПП, изменяется не мгновенно (темп его изменения соизмерим с темпом изменения скорости привода в ПП-се); учитывается только мех-кая инерция в приводе (J), индуктивности в цепях двигателя малы или не проявляются. Типичные структуры системы П-Д и соответствующие мех-кие хар-ки показаны на рис. 5.11”а” и “в”.

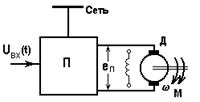
а) б) в) г)

Рис. 5.11 – а и б) Система ПН-ДПТ и ее мех-кие хар-ки;

в и г) Система ПЧ-АД и ее мех-кие хар-ки

Роль преобразователя П в схеме на рис.5.11 а может играть генератор (система Г-Д) или тиристорный преобразователь (ТП-Д). Фактор, вызывающий ПП в этих системах, – изменение входного сигнала u_вх, приводящее к изменению ЭДС преобразователя е_п.

Роль преобразователя П в схеме на рис.5.11 в играет статический преобразователь частоты. Фактор, вызывающий ПП в этих системах, – изменение входного сигнала u_вх, приводящее к изменению частоты и напряжения на выходе преобразователя.