Означення. Лінйним оператором у векторному просторі 
називається відображення векторного простору в себе 
→ таке, що виконані наступні умови (умови лінійності):
1) 
;
1) 
;
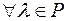
Лінійний оператор називається також лінійним перетворенням векторного простору .
Означення. Матрицею лінійного оператора 
в базисі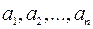 
називається матриця
,
елементами якої є коефіцієнти в розкладі образів векторів 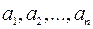за базисом 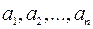, тобто
;
;
………………………………………..
.
З означення випливає, що стовпцями матриці 
є координатні рядки векторів 
, 
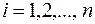, в базисі .
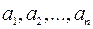При фіксованому базисі 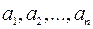кожному лінійному оператору простору відповідає певна матриця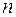 
-го порядку – матриця цього лінійного оператора. Справедливе і обернене: кожна матриця 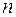-го порядку є матрицею певного лінійного оператора простору в базисі .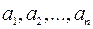
У координатному вигляді дія лінійного оператора на вектор 
зводиться до множення матриці лінійного оператора на координатний стовпчик вектора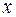 
:
.
Власні значення і власні вектори лінійного оператора
Нехай – векторний простір, а – лінійний оператор в цьому просторі.
Означення. Число 
називається власним значенням лінійного оператора , якщо існує ненульовий вектор 
, такий, що 
. Вектор 
називається власним вектором лінійного оператора , який відповідає власному значенню 
.
З означення випливає, що лінійний оператор переводить власний вектор в йому пропорційний вектор.
Нехай 
– матриця порядку , 
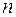– одинична матриця порядку 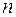, – деяке невідоме.
Означення. Характеристичним многочленом матриці називається многочлен 
, визначений рівністю:
.
Означення. Характеристичним многочленом лінійного оператора називається характеристичний многочлен його матриці.
Теорема (про власні значення лінійного оператора). Кожне власне значення лінійного оператора є коренем його характеристичного многочлена і навпаки, кожний корінь характеристичного многочлена є власним значенням лінійного оператора .
На практиці координати власного вектора , який відповідає певному власному значенню визначають як ненульовий розв’язок однорідної системи лінійних алгебраїчних рівнянь
.
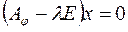Приклад. Знайти власні значення і власні вектори лінійного оператора , який заданий в деякому базисі матрицею
.
Розв’язання. 1) Складемо характеристичний многочлен і визначимо його корені:
;
; 
; 
, 
.
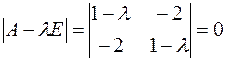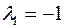Отже, 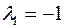, – власні значення лінійного оператора.
2) Визначимо координати власних векторів:
Для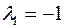
; 
, 
, 
.
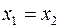Отже, власному значенню 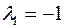відповідає власний вектор , .
Для
;
; 
, 
, 
.
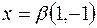Отже, власному значенню відповідає власний вектор , .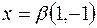
Домашнє завдання: вивчити питання лекції.
