Статистика как наука. Предмет, метод и задачи статистики
Актуальность
В жизни сталкиваемся с результатами статистических исследований:
- рейтинги;
- переписи населения;
- прогнозы (экономический, метеорологический, политический, социальный и др.);
- индексы динамики различных показателей.
Органы статистики:
- Госкомстат (управления по статистике);
- органы ЗАГС.
Статистика – самостоятельная, имеющая свой предмет и метод исследования наука. Возникла она из практических потребностей общественной жизни. Уже в древнем мире появилась потребность подсчитывать численность жителей государства, учитывать людей, пригодных к военному делу, определять количество скота, размеры земельных угодий и другого имущества. Информация такого рода была необходима для сбора налогов, ведения войн и т.п. В дальнейшем, по мере развития общественной жизни, круг учитываемых явлений постепенно расширяется.
Особенно возрастает объем собираемой информации с развитием капитализма и мирохозяйственных связей. Потребности этого периода вынуждали органы государственного управления и капиталистические предприятия собирать для практических нужд обширную и разнообразную информацию о рынках труда и сбыта товаров, сырьевых ресурсах.
В середине 17-го века в Англии возникло научное направление, получившее название " политической арифметики ". Начало этому направлению положили Вильям Петти (1623-1687 гг.) и Джон Граунт (1620-1674 гг.). "Политические арифметики" на основе изучения информации о массовых общественных явлениях стремились открыть закономерности общественной жизни и, таким образом, ответить на вопросы, возникавшие в связи с развитием капитализма.
Наряду со школой "политических арифметиков" в Англии, в Германии развивалась школа описательной статистики или " государствоведения ". Возникновение этой науки относится к 1660 г.
Развитие политической арифметики и государствоведения привело к появлению науки статистики.
Понятие "статистика" происходит от латинского слова "status", которое в переводе означает – положение, состояние, порядок явлений.
В научный оборот термин "статистика" ввел профессор Геттингенского университета Готфрид Ахенваль (1719-1772 гг.) в середине 18 века.
Статистика как наука исследует не отдельные факты, а массовые явления и процессы, выступающие как множество отдельных факторов, обладающих как индивидуальными, так и общими признаками.
Предмет статистики
Статистика, вернее ее методы исследования, широко применимы в различных областях человеческих знаний. Однако, как любая наука, она требует определения предмета исследования.
Предмет (объект) статистического исследования в статистике называют статистической совокупностью. Статистическая совокупность – это множество единиц, обладающих массовостью, однородностью, определенной целостностью, взаимозависимостью состояния отдельных единиц и наличием вариации.
Каждый отдельный элемент данного множества называется единицей статистической совокупности.
В зависимости от объекта (предмета) изучения статистика как наука подразделяется на социальную, демографическую, экономическую, промышленную, торговую, банковскую, финансовую, медицинскую и т.д. Общие свойства статистических данных, независимо от их природы, и методы их анализа рассматриваются математической статистикой и общей теорией статистики.
В нашем курсе речь будет идти о так называемой прикладной статистике - т.е. только о сущности специальных методов сбора, обработки и анализа информации и, кроме того, о практических приемах выполнения связанных с этим расчетов.
Статистика как наука имеет дело прежде всего с количественной стороной явлений и процессов в конкретных условиях места и времени. Одной из характерных особенностей статистики является то, что при изучении количественной стороны явлений и процессов она всегда отображает качественные особенности исследуемых явлений, т.е. изучает количество в неразрывной связи, единстве с качеством.
Статистическая методология
Важнейшими составными элементами статистической методологии являются:
1) массовое статистическое наблюдение (сбор первичных данных);
2) статистическая сводка (группировка) первичных данных, получение обобщающих (сводных) характеристик;
3) получение обобщающих статистических параметров, обнаружение закономерностей в изучаемых явлениях;
4) оценка достоверности (значимости) обнаруженных закономерностей.
Содержание перечисленных выше пунктов определяют этапы проведения любого статистического исследования:
1. Чтобы охарактеризовать с количественной стороны любое массовое явление, необходимо сначала собрать информацию о составляющих его элементах. Это и достигается при помощи массового наблюдения, осуществляемого на основе выработанных статистической наукой правил и способов.
2. Собранные в процессе статистического наблюдения сведения подвергаются в дальнейшем сводке (первичной научной обработке), в процессе которой из всей совокупности обследованных единиц выделяются характерные части (группы). Выделение групп единиц из всего обследуемого множества называется в статистике группировкой. Группировка в статистике является основой обработки и анализа собранной информации. Осуществляется она на основе определенных принципов и правил.
3. В процессе обработки статистической информации совокупность обследованных единиц и выделенные ее части на основе применения метода группировок характеризуются системой цифровых показателей: абсолютных и средних величин, относительных величин, показателей динамики и т.д.
4. Современная статистика добилась больших успехов в разработке объективных методов проверки значимости результатов. Основной задачей многих статистических исследований является отделение действительных эффектов от случайных.
Задача статистики
Основной задачей статистики является сбор, учет, обработка и хранение данных (информации) из области человеческой деятельности и природных явлений.
Основные понятия и категории статистики
Человек воспринимает окружающую среду как непрерывную последовательность событий. Он анализирует поступающую информацию и (хотя и не всем это удается) делает выводы из такого анализа и учитывает их в своей сознательной деятельности. Поэтому можно смело утверждать, что во все времена люди занимались и занимаются статистическими “исследованиями”, даже не зная иногда такого слова - “статистика”.
Случайное событие – событие, которое при заданном комплексе факторов может произойти, а может не произойти.
Не задерживаясь на раскрытии философской сущности термина “случайность” (вполне достаточно обычное, житейское представление), обратимся к чрезвычайно важному понятию - вероятность. Этот термин обычно используют по отношению к событию и определяют числом (от 0 до 1), выражающим степень нашей уверенности в том, что данное событие произойдет.
Вероятность – числовая характеристика степени возможности наступления какого-либо определенного события в тех или иных определенных условиях, могущих повторяться неограниченное число раз. Вероятность (Р) равна отношению числа благоприятных для данного события исходов (m) к общему числу равновозможных исходов (n).

Достоверное событие – событие, которое при заданном комплексе факторов обязательно произойдет (хотя это уже – неслучайное, детерминированное события). Р (А) = 1.
Невозможное событие – событие, которое не может осуществиться при заданном комплексе факторов. Р (В) = 0.
Независимые события – события, для которых появление или отсутствие одного из них никак не сказывается на вероятности появления другого.
Будем толковать случайное событие А как попадание точки в некоторую область (А) квадрата (рис. 1, а).
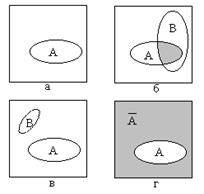
Рис. 1.
Сумма (объединение) событий А,+ А2 +…+ Аn – событие, которое имеет вид: наступает или А1, или А2, …, или Аn (т.е. хотя бы одно из событий Аi). Тогда рис. 1, б иллюстрирует понятие суммы С = А + В (попадание в область, являющуюся объединением областей А и В).
Р (С) = Р (А+В) = Р ( ) = Р (А) + Р (В).
) = Р (А) + Р (В).
Произведение (совмещение) событий А1, А2, …, Аn – событие, которое имеет вид: наступает и А1, и А2, …, и Аn. На рисунке совмещение событий можно толковать как попадание точки в общую часть областей А и В (на рис. 1, б эта общая часть помечена серым цветом).
Р (А×В) = Р ( ) = Р (А) × Р (В), если А и В - независимы.
) = Р (А) × Р (В), если А и В - независимы.
Несовместные события – события, одновременное осуществление которых невозможно (см. рис. 1, в – области А и В не имеют общих точек, поэтому никакая точка не может попасть одновременно в обе эти области). Р (А×В) = 0.
Противоположные события А и  – события, для которых одно из них проявляется тогда и только тогда, когда другое отсутствует (на рис. 1, г область противоположного события
– события, для которых одно из них проявляется тогда и только тогда, когда другое отсутствует (на рис. 1, г область противоположного события  помечена серым цветом).
помечена серым цветом).  = 1. Если Р(А) = р, то
= 1. Если Р(А) = р, то  = q = 1- р.
= q = 1- р.
Иногда в прикладной статистике приходится иметь дело с так называемыми редкими маловероятнымисобытиями. К ним принято относить события, значение вероятности которых не превышает определенного уровня, чаще всего – 0.05 или 5 %.
Наблюдаемые нами значения показателей, характеризующих присущие случайным событиям свойства, называются в статистике признаками. По форме выражения признаки делятся на атрибутивные (описательные, качественные) и количественные.

Атрибутивные (качественные) признаки не поддаются количественному (числовому) выражению. Количественные признаки выражают через числа, которые являются случайными величинами (далее везде – СВ).Случайные величины делят на две разновидности:

Дискретные СВ могут принимать только конкретные, заранее оговоренные значения (например, - значения чисел на верхней грани брошенной игральной кости или порядковые значения текущего месяца). Дискретная случайная величина – это СВ, для которой совокупность возможных значений конечна или поддается счислению.
Непрерывные СВ (чаще всего - значения некоторых физических величин: веса, расстояния, температуры и т.п.) могут принимать любые значения, хотя бы и в некотором интервале. Непрерывная случайная величина – это СВ, совокупность возможных значений которых бесконечна или не поддается счислению.
Случайная величина – это некоторая переменная величина, принимающая в зависимости от случая те или иные значения Хi (X1, X2, …, Xn) с определенными вероятностями Pi (P1, P2, …, Pn). Случайные величины могут также называться данными.
 .
.
Ранее уже говорилось, что предметом статистического исследования является статистическая совокупность случайных величин Хi..






