Ранее говорилось, что звено в ТАУ считается однонаправленным, т.е. преобразует сигнал в одном направлении. Если ввести дополнительное предположение о независимости передаточных функций отдельных звеньев от их соединения (или определять передаточную функцию звена с учетом соединения), то любая линейная САУ может быть сведена к схеме показанной на рис.3.9.
Рис.3.9. Эквивалентная структурная схема линейной САУ.
Согласно данной схеме:
, (3.18)
где 
— эквивалентная передаточная функция.
Отметим, что с математической точки зрения замена соединения звеньев одним звеном с эквивалентной передаточной функцией соответствует исключению промежуточных переменных в системе уравнений, описывающих это соединение.
Различают три вида соединения звеньев: последовательное, параллельное и соединение с обратной связью.
Последовательным соединением звеньев называется такое соединение, когда выходная величина предыдущего звена является входной величиной последующего звена (рис.3.10).
Рис.3.10. Последовательное соединение звеньев.
Найдем эквивалентную передаточную функцию для данного соединения звеньев. Из рис.3.10 следует:
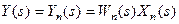. (3.19)
Согласно определению последовательного соединения звеньев:
. (3.20)
Подставляя последовательно (3.20) в (3.19) можно записать:
. (3.21)
Разделим обе части (3.21) на 
:
.
Таким образом, последовательное соединение n звеньев с передаточными функциями 
(i = 1,2,..., n) может быть заменено звеном с эквивалентной передаточной функцией
. (3.22)
Перейдем от передаточных функций к КЧХ звеньев системы, т.е. произведем замену 
, получим
(3.23)
Представим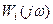 
в показательном виде:
,
и подставим их в (3.23):
.
Отсюда определяем, что эквивалентные АЧХ и ФЧХ для случая последовательного соединения звеньев находятся:
, (3.24)
. (3.25)
Таким образом, при последовательном соединении звеньев АЧХ перемножаются, а и ФЧХ складываются.
Параллельным соединением звеньев называется такое соединение, когда на входы всех звеньев подается одна и та же величина, а выходные сигналы суммируются. Если параллельно соединены n звеньев (рис. 3.11), то входной сигнал
(3.26)
а выходной
(3.27)
Рис.3.11. Параллельное соединение звеньев.
Переходя в (3.26), (3.27) к изображениям c учетом того, что 
, получим
,
т.е.
(3.28)
Очевидно, что такое же правило справедливо для переходных и импульсных переходных характеристик (вспомним связь между этими характеристиками и передаточной функцией):
, (3.29)
. (3.30)
Эквивалентную КЧХ системы найдем, выполнив в (3.28) замену :
. (3.31)
Если представить 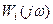в виде суммы действительной и мнимой составляющей
,
то подставив данное выражение в (3.31) найдем
, (3.32)
где 
, 
.
Теперь пользуясь формулами (3.77) можно найти эквивалентные АЧХ и ФЧХ.
Соединение с обратной связью. О наличии обратной связи в системе говорят, когда сигнал с выхода одного звена посредством другого звена (звеньев) подается обратно на его вход (рис.3.12).
Рис.3.12. Соединение звеньев с обратной связью.
Участок схемы (цепи) от сумматора и до точки съема выходного сигнала y называется прямой связью (передачей), а участок схемы от точки съема выходного сигнала до сумматора – обратной связью. Звенья с передаточными функциями 
и 
называются соответственно звеном прямой и обратной связи.
Сигнал обратной связи x2 может либо суммироваться с входным воздействием x, либо вычитаться из него, то есть:
или в изображениях
. (3.33)
В первом случае говорят о наличии положительной, а во втором – отрицательной обратной связи.
Определим формулу нахождения эквивалентной передаточной функции при соединении звеньев с обратной связью. Изображение выходной величины системы связано с изображением входного воздействия уравнением:
откуда следует:
,
где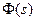 
— передаточная функция системы с обратной связью, которая связана с передаточными функциями звеньев данной системы соотношением:
. (3.34)
Знак " минус " относится к системе с положительной обратной связью, а знак " плюс " — к системе с отрицательной обратной связью.
Рассматриваемая структура отличается от двух предыдущих (последовательное и параллельное соединение) тем, что она содержит замкнутый контур циркуляции сигнала; поэтому такую систему называют еще замкнутой.
Формулу (3.34) обычно записывают в следующем виде:
, (3.35)
где
(3.36)
— передаточная функция разомкнутого контура системы.
Передаточная функция 
соответствует структуре полученной из исходной замкнутой системы (рис.3.12), если разомкнуть ее сразу после сумматора. При этом получается схема из двух последовательно соединенных звеньев, как это показано на рис.3.13.
Рис.3.13. Вид соединения звеньев после размыкания замкнутого контура.
Очевидно, что связь между указанными входным x1 и выходным x2 сигналами и будет определяться передаточной функцией .
Если в системе с отрицательной обратной связью устремить коэффициент передачи звена в прямой передаче сигнала к бесконечности, то свойства такой системы становятся независимыми от свойств этого звена и определяются только свойствами обратной связи. Действительно, если в (3.34) устремить 
, получим:
. (3.37)
Это интересное свойство сохраняется и в случае, когда в прямой передаче сигнала находится нелинейное звено.
Рассмотрим систему управления изображенную на рис.3.14. На данном рисунке 
— передаточная функция командного блока; 
– передаточная функция регулятора; 
– передаточная функция ОУ, определяющая влияние управляющего воздействия 
на управляемую величину 
; 
– передаточная функция ОУ, определяющая влияние возмущающего воздействия 
на .
Рис.3.14. Структурная схема системы управления.
Данная система управления по каналу действия входного сигнала x(t) на управляемую величину y(t) представляет собой последовательное включение командного блока (КБ) и подсистемы регулирования с обратной связью (ОС). Поэтому, в соответствии с (3.22), ее передаточная функция определяется:
, (3.38)
где 
— передаточная функция подсистемы регулирования по каналу действия задающего воздействия g(t) на регулируемую величину y(t).
Входными воздействиями подсистемы регулирования кроме задающего воздействия g(t) могут быть и возмущения (число которых может быть произвольным), а выходными параметрами, помимо регулируемой величины y(t), могут быть также ошибка регулирования 
и регулирующее (управляющее) воздействие . Следовательно, рассматриваемая подсистема регулирования с одной управляемой величиной y(t) обладает несколькими передаточными функциями, которые выражаются через передаточные функции звеньев данной подсистемы регулирования формулой (3.35):
1) по каналу " задающее воздействие — регулируемая величина " (рис.3.14):
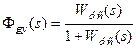; (3.39)
2) по каналу " задающее воздействие — ошибка регулирования " (рис.3.15):
; (3.40)
Рис.3.15. Передача воздействия по каналу " задающее воздействие — ошибка регулирования ".
3) по каналу " возмущение — регулируемая величина " (рис.3.16):
. (3.41)
Рис.3.16. Передача воздействия по каналу " возмущение — регулируемая величина ".
Во всех последних формулах (3.39 – 3.41):
(3.42)
— передаточная функция разомкнутого контура.
При комбинированном включении звеньев в САУ следует использовать совместно формулы (3.22), (3.28) и (3.35).
Рис.3.17. Пример комбинированного соединения звеньев.
Пример. Найдем эквивалентную передаточную функцию системы, изображенной на рис.3.17. Заменим параллельно соединенные звенья с передаточными функциями W2(s) и W7(s) на звено с передаточной функцией:
.
Участок замкнутой системы, состоящий из цепи прямой связи с передаточной функцией:
и цепи обратной связи W8(s) имеет эквивалентную передаточную функцию:
.
В результате приходим к замкнутой системе с последовательно соединенными звеньями W1(s), WЭ1(s), WЭ3(s), W5(s), W6(s) в цепи прямой связи, которые в свою очередь заменим эквивалентным звеном с передаточной функцией:
и пропорциональным звеном с передаточной функцией 
в цепи обратной связи. Окончательно имеем:
.
