СТРУКТУРНЫЕ СХЕМЫ ЛИНЕЙНЫХ САУ
Типовые звенья линейных САУ
Любые сложные САУ могут быть представлены как совокупность более простых элементов (вспомним функциональные и структурные схемы). Поэтому для упрощения исследования процессов в реальных системах они представляются в виде совокупности идеализированных схем, которые точно описываются математически и приближенно характеризуют реальные звенья систем в определенном диапазоне частот сигналов.
При составлении структурных схем вводятся некие типовые элементарные звенья (простые, далее не делимые), характеризующиеся только своими передаточными функциями, вне зависимости от их конструктивного исполнения, назначения и принципа действия. Классифицируют их по видам уравнений описывающих их работу. В случае линейных САУ различают следующие типы звеньев:
1.Описываемые линейными алгебраическими уравнениями относительно выходного сигнала:
а) пропорциональное (статическое, безынерционное);
б) запаздывающее.
2.Описываемые дифференциальными уравнениями первого порядка с постоянными коэффициентами:
а) дифференцирующее;
б) инерционно-дифференцирующее (реальное дифференцирующее);
в) инерционное (апериодическое);
г) интегрирующее (астатическое);
д) интегро-дифференцирующее (упругое).
3.Описываемые дифференциальными уравнениями второго порядка с постоянными коэффициентами:
а) инерционное звено второго порядка (апериодическое звено второго порядка, колебательное).
Используя математический аппарат, изложенный выше, рассмотрим передаточные функции, переходные и импульсные переходные (весовые) характеристики, а также частотные характеристики этих звеньев.
Приведем формулы, которые будут использованы для этой цели.
1. Передаточная функция: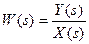 
.
2. Переходная характеристика: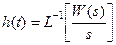 
.
3. Импульсная переходная характеристика: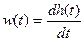 
или 
.
4. КЧХ: 
.
5. Амплитудная частотная характеристика: 
,
где 
, 
.
6. Фазовая частотная характеристика: 
.
По этой схеме и исследуем типовые звенья.
Заметим, что хотя для некоторых типовых звеньев n (порядок производной выходного параметра в левой части уравнения) равняется m (порядок производной входного параметра в правой части уравнения), а не больше m, как говорилось ранее, однако при конструировании реальных САУ из этих звеньев условие m<n для всего САУ обычно всегда выполняется.
Пропорциональное (статическое, безынерционное) звено. Это самое простое звено, выходной сигнал которого прямо пропорционален входному сигналу:
(3.1)
где k — коэффициент пропорциональности или передачи звена.
Примерами такого звена являются: а) клапаны с линеаризованными характеристиками (когда изменение расхода жидкости пропорционально степени изменения положения штока) в рассмотренных выше примерах систем регулирования; б) делитель напряжения; в) рычажная передача и др.
Переходя в (3.1) к изображениям, имеем:
1. Передаточная функция: 
.
2. Переходная характеристика: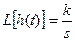 
, следовательно 
.
3. Импульсная переходная характеристика: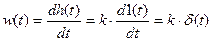 
.
4. КЧХ: 
.
5. АЧХ: 
.
6. ФЧХ: 
.
Принятое описание связи между входом и выходом справедливо только для идеального звена и соответствует реальным звеньям лишь при низких частотах, 
. При 
в реальных звеньях коэффициент передачи k начинает зависеть от частоты и при высоких частотах падает до нуля.
Запаздывающее звено. Это звено описывается уравнением
, (3.2)
где 
– время запаздывания.
Примером запаздывающего звена служат: а) длинные электрические линии без потерь; б) длинный трубопровод и др.
Передаточная функция, переходная и импульсная переходная характеристика, КЧХ, а также АЧХ и ФЧХ этого звена:
1. 
.
2. 
, значит: 
.
3. 
.
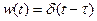4. 
.
5. 
.
6. 
.
На рис.3.1 изображены: а) годограф КЧХ запаздывающего звена; б) АЧХ и ФЧХ запаздывающего звена. Заметим, что при увеличении 
конец вектора описывает по часовой стрелке все возрастающий угол.
Рис.3.1. Годограф (а) и АЧХ, ФЧХ (б) запаздывающего звена.
Интегрирующее звено. Это звено описывается уравнением
или (3.3)
.
где 
— коэффициент передачи звена.
Примерами реальных элементов, эквивалентные схемы которых сводятся к интегрирующему звену, являются: а) электрический конденсатор, если считать входным сигналом ток, а выходным – напряжение на конденсаторе: 
; б) вращающийся вал, если считать входным сигналом угловую скорость вращения, а выходным – угол поворота вала: 
; и т.д.
Определим характеристики данного звена:
1. 
.
2. 
.
Воспользуемся таблицей преобразования Лапласа 3.1, получаем:
.
Умножаем на 
так как функция 
при 
.
3. 
.
4. 
.
5. 
.
6. 
.
На рис.3.2 показаны: а) годограф КЧХ интегрирующего звена; б) АЧХ и ФЧХ звена; в) переходная характеристика звена.
Рис.3.2. Годограф (а), АЧХ и ФЧХ (б), переходная характеристика (в) интегрирующего звена.
Дифференцирующее звено. Это звено описывается уравнением
, (3.4)
где 
– коэффициент передачи звена.
Найдем характеристики звена:
1. 
.
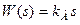2. 
, учитывая, что 
, находим: 
.
3. 
.
4. 
.
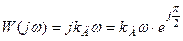5. 
.
6. 
.
На рис.3.3 показаны: а) годограф звена; б) АЧХ и ФЧХ звена.
а) б)
Рис. 3.3. Годограф (а), АЧХ и ФЧХ (б) дифференцирующего звена.
Примером дифференцирующего звена являются идеальный конденсатор и индуктивность. Это следует из того, что напряжение u и ток i связаны для конденсатора С и индуктивности L соответственно следующими соотношениями:
, 
.
Отметим, что реальная емкость обладает небольшой емкостной индуктивностью, реальная индуктивность имеет межвитковую емкость (которые особенно сильно проявляются на больших частотах), что приводит указанные выше формулы к следующему виду:
, 
.
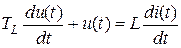Таким образом, дифференцирующее звено не может быть технически реализовано, так как порядок правой части его уравнения (3.4) больше порядка левой части. А нам известно, что должно выполняться условие n > m или, в крайнем случае, n = m.
Однако можно приблизиться к этому уравнению данного звена, использовав инерционно-дифференцирующее (реальное дифференцирующее) звено.
Инерционно-дифференцирующее (реальное дифференцирующее) звено описывается уравнением:
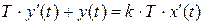, (3.5)
где k — коэффициент передачи звена, Т — постоянная времени.
Передаточная функция, переходная и импульсная переходная характеристики, КЧХ, АЧХ и ФЧХ этого звена определяются формулами:
1. 
.
2. 
.
Используем свойство преобразования Лапласа – смещение изображения (3.20), согласно которому: если 
, то 
.
Отсюда: 
.
3. 
.
4. 
.
5. 
.
6. 
.
На рис.3.4 приведены: а) график КЧХ; б) АЧХ и ФЧХ звена.
а) б)
Рис.3.4. Годограф (а), АЧХ и ФЧХ реального дифференцирующего звена.
Для того чтобы свойства реального дифференцирующего звена приближались к свойствам идеального, необходимо одновременно увеличивать коэффициент передачи k и уменьшать постоянную времени Т так, чтобы их произведение оставалось постоянным:
kT = k д,
где k д – коэффициент передачи дифференцирующего звена.
Отсюда видно, что в размерность коэффициента передачи k д дифференцирующего звена входит время.
Инерционное звено первого порядка (апериодическое звено) одно из самых распространенных звеньев САУ. Оно описывается уравнением:
, (3.6)
где k – коэффициент передачи звена, Т – постоянная времени.
Характеристики данного звена определяются формулами:
1. 
.
2. 
.
Пользуясь свойствами интегрирования оригинала и смещением изображения имеем:
.
3. 
, т.к. 
при 
, то на всей временной оси данная функция равна 0 (
при 
).
4. 
.
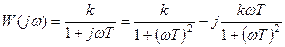5. 
.
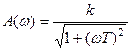6. 
.
На рис.3.5 показаны: а) график КЧХ; б) АЧХ и ФЧХ звена.
Рис.3.5. Годограф (а), АЧХ и ФЧХ инерционного звена первого порядка.
Интегро-дифференцирующее звено. Это звено описывается дифференциальным уравнением первого порядка в наиболее общем виде:
, (3.7)
где k — коэффициент передачи звена, Т1 и Т2 — постоянные времени.
Введем обозначение:
.
В зависимости от значения t звено будет обладать различными свойствами. Если 
, то звено по своим свойствам будет приближаться к интегрирующему и инерционному звеньям. Если 
, то данное звено по свойствам будет ближе к дифференцирующему и инерционно-дифференцирующему.
Определим характеристики интегродифференцирующего звена:
1. 
.
2. 
, отсюда следует:
.
3. 
, т.к. 
при t ® 0, то:
.
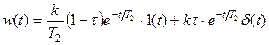4. 
.
5. 
.
6. 
.
На рис.3.6. приведены: а) график КЧХ; б) АЧХ; в) ФЧХ; г) переходная характеристика звена.
а) б)
в) г)
Рис.3.6. Годограф (а), АЧХ (б), ФЧХ (в), переходная характеристика (г) интегродифференцирующего звена.
Инерционное звено второго порядка. Это звено описывается дифференциальным уравнением второго порядка:
, (3.8)
где 
(капа) – постоянная затухания; Т — постоянная времени, k — коэффициент передачи звена.
Реакция системы, описываемой уравнением (3.8), на единичное ступенчатое воздействие при 
представляет собой затухающие гармонические колебания, в этом случае звено еще называется колебательным. При 
колебания не возникнут, и звено, описываемое уравнением (3.8) называется апериодическим звеном второго порядка. Если 
, то колебания будут незатухающими с частотой 
.
Примером конструктивного выполнения данного звена могут служить: а) электрический колебательный контур, содержащий емкость, индуктивность и омическое сопротивление; б) масса, подвешенная на пружине и имеющая демпфирующее устройство, и т.д.
Определим характеристики инерционного звена второго порядка:
1. 
.
2. 
.
Корни характеристического уравнения стоящего в знаменателе определяются:
.
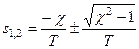Очевидно, что здесь возможно три случая:
1) при 
корни характеристического уравнения отрицательные вещественные разные 
и 
, тогда переходная характеристика определяется:
;
2) при 
корни характеристического уравнения отрицательные вещественные одинаковые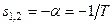 
:
;
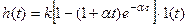3) при 
корни характеристического уравнения звена являются комплексно - сопряженными 
, причем
, 
, (3.9)
переходная характеристика определяется формулой:
,
т.е., как отмечалось выше, она приобретает колебательный характер.
3. Также имеем три случая:
1) 
,
т.к. 
при 
;
2) 
, т.к. 
при ;
3) 
, т.к. 
при .
4. 
.
5. 
.
6. 
,
где а = 0 при 
и а = 1 при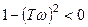 
(см. формулу (3.77)).
а) б)
Рис.3.7. График КЧХ (а) и переходная характеристика (б) звена.
На рис.3.7, а, б показан типичный вид КЧХ и переходных характеристик для случаев 
и . Согласно рисунку уменьшение значения приводит к тому, что петля, очерченная концом вектора , увеличивается. При , т.е. при наличии в системе незатухающих колебаний, петля вырождается в две полупрямые: первая от =k при 
до 
при 
(приближаемся слева, т.е. 
и 
) и вторая от 
при (приближаемся справа, т.е. 
и 
) до 
при 
.
На рис.3.8 показаны соответствующие АЧХ и ФЧХ. Здесь 
– безразмерная частота.
а) б)
Рис.3.8. АЧХ (а) и ФЧХ (б) звена.
Как видим, колебательному характеру переходной характеристики соответствует наличие в графике АЧХ резонансного пика при частоте резонанса 
. Отношение максимального (пикового) значения АЧХ к ее значению при нулевой частоте получило название частотного показателя колебательности:
. (3.10)
Продифференцируем выражение для АЧХ этого звена по , и приравняем производную к нулю. В результате получим выражение для резонансной частоты системы
при условии 
, (3.11)
Из (3.11) следует, что при 
резонансная частота 
, а, согласно формуле для АЧХ, при этом 
.
Подстановка (3.11) и выражения для АЧХ в (3.10) приводит к следующей формуле для определения частотного показателя колебательности:
при условии . (3.12)
Об интенсивности затухания колебаний можно судить также и по корневому показателю колебательности, который равен отношению абсолютного значения вещественной части корней к их мнимой части:
.
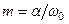С учетом (3.9) корневой показатель колебательности т рассматриваемого звена можно выразить через коэффициенты его уравнения:
. (3.13)
Приняв во внимание (3.12), можно установить связь т с частотным показателем колебательности M:
. (3.14)
На практике интенсивность затухания колебаний в колебательном звене удобно характеризовать относительным уменьшением соседних амплитуд 
и 
переходной характеристики (рис.3.7, б):
. (3.15)
Этот показатель получил название степени затухания колебаний.
Поскольку переходная характеристика колебательного звена определяется формулой:
,
то можно записать:
, (3.16)
где 
— период собственных колебаний звена.
С учетом этого формулу (3.15) можно представить следующим образом:
. (3.17)
Таким образом, степень затухания однозначно связана с корневым показателем колебательности т,а, следовательно, и с частотным показателем колебательности М.
