Дробно-линейное программирование

Дробно-линейное программирование относится к нелиней­ному программированию, так как имеет целевую функцию, за­данную в нелинейном виде.

Задача дробно-линейного программирования в общем виде записывается следующим образом:

при ограничениях:

 

где c_j, d_j, b_i, a_ij — постоянные коэффициенты и d_jx_j ≠0.

Данная задача довольно трудная, решение которой выходит за рамки данного курса математики. Укажем для любознательных алгоритм решения таких задач.

1. Находится область допустимых решений.

2. Определяется угловой коэффициент k и устанавливаем на­правление поворота целевой функции.

3. Находится точка max(min) целевой функции или устана­вливаем неразрешимость задачи.

 

Математическая модель задачи дробно-линейного програм­мирования может быть использована для определения рента­бельности затрат на производство изделий, рентабельности продаж, затрат в расчете на рубль выпускаемой продукции, себестоимости изделий.

 

Рассмотрим использование дробно-линейного программи­рования для нахождения себестоимости изделий.

Пример 6. Для производства двух видов изделий А и В пред­приятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов оборудования. Время обработки каждого из изделий, затраты, связанные с производством одного изделия, даны в табл. 28.1

Оборудование I и III типов предприятие может использо­вать не более 26 и 39 ч соответственно, оборудование II типа целесообразно использовать не менее 4 ч.

Определить, сколько изделий каждого вида следует изго­товить предприятию, чтобы средняя себестоимость одного из­делия была минимальной.

Решение. Пусть x ₁ — количество изделий вида А, которое следует из­готовить предприятию, x ₂ — количество изделий вида В. Об­щие затраты на их производство составят (2 х ₁ + 3 x ₂) тыс. р., а средняя себестоимость одного изделия будет равна

Математическая модель задачи примет вид

при ограничениях:

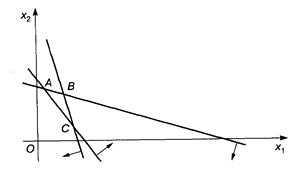
Δ АВС — область допустимых решений

Найдем x ₂: L = (2 x ₁ + 3 x ₂) / (x ₁ + x ₂), 2 x ₁ + 3 х ₂ = Lx ₁ + Lx ₂, x ₂ (3 - L) = x ₁(L - 2),

Угловой коэффициент прямой равен k = (L - 2)/(3 — l), тогда

 

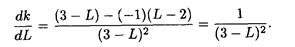
Так как dk/dL > 0, то функция k = (L - 2)/(3 - L) возрастает. Это соответствует вращению прямой против часовой стрелки. Следовательно, в точке С (рис.) целевая функция будет иметь наименьшее значение (глобальный минимум).

Найдем координаты точки С. Решая систему, получим С (3, 1),

_опт = (3, 1), L =9/4.

Следовательно, предприятию следует выпускать 3 изделия вида А и 1 изделие вида В. При этом средняя себестоимость одного изделия будет минимальной и равной 2,25 тыс. р.

Задачу дробно-линейного программирования можно свести к задаче линейного программирования и решить симплексным методом.

 

Метод множителей Лагранжа

Дана задача нелинейного программирования

при ограничениях:

Предположим, что функции f (x ₁, х ₂ ,..., x_п) и g_i(x ₁, x ₂,..., x_п) непрерывны вместе со своими первыми частными про­изводными.

Ограничения заданы в виде уравнений, поэтому для ре­шения задачи воспользуемся методом отыскания условного эк­стремума функции нескольких переменных.

Для решения задачи составляется функция Лагранжа

где λ _i — множители Лагранжа.

Пояснения. Функция Лагранжа есть сумма целевой функции и ограничений, умноженных на множитель, который будет получен при решении системы составленной из частных производных функции Лагранжа

Затем определяются частные производные:

Приравняв к нулю частные производные, получим систему

Решая систему, получим множество точек, в которых целевая функция L может иметь экстремальные значения. Следует отметить, что условия рассмотренной системы являются необходимыми, но недостаточными. Поэтому не всякое полученное решение определяет точку экстремума целевой функции. Применение метода бывает оправданным, когда заранее предполагается существование глобального экстремума, совпадающего с единственным локальным максимумом или минимумом целевой функции.

Пример 8. Найти точку условного экстремума функции

Ограничения:

Решение. Составим функцию Лагранжа:

 

Пояснения. Для составления функции Лагранжа запишем ограничения в виде: q₁=x₁-x₂-2 и q₂=x₂+2x₃-4. Функция Лагранжа есть сумма целевой функции и ограничений, умноженных на множитель, который будет получен при решении системы составленной из частных производных функции Лагранжа.

Найдем частные производные функции Лагранжа по пере­менным x ₁, x ₂, x ₃, λ₁, λ₂. Приравняв к нулю полученные вы­ражения, решим систему

λ₁ = - x ₂, λ₂ = - x ₂/2,

х ₁ = -2, x ₂ = -4, x ₃ = 4, L = -8.

Определим характер экстремума, изменяя полученные зна­чения переменных.

Измененные значения должны удовлетво­рять заданной системе ограничений.

Возьмем х ₁ > -2, напри­мер x ₁ = -1, тогда из системы ограничений получим х ₂ = -3, x ₃ = 7/2, L = -15/2.

Возьмем х ₁ < -2, например х ₁ = -3, тогда получим х ₂ = -5, x ₃ = 9/2, L = -15/2.

Следовательно, L = -8 — минимальное значение функции.

Ответ. Точка экстремума х ₁ = -2, x ₂ = -4, x ₃ = 4, максимальное значение функции L = -8.

 

Пример 9. Мукомольный комбинат реализует муку двумя способами: в розницу через магазин и оптом через торговых агентов.

При продаже x ₁ кг муки через магазин расходы на реализацию составляют х ₁² руб., а при продаже x ₂ кг муки посредством торговых агентов — х ₂² руб.

Определить, сколько килограммов муки следует продавать каждым способом, чтобы затраты на реализацию были мини­мальными, если в сутки выделяется для продажи 5 000 кг муки.

Решение. Составим математическую модель задачи.

Найдем минимум суммарных расходов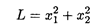

Ограничения:

Для расчета модели используем метод множителей Лагранжа. Составим функцию Лагранжа

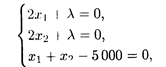
Найдем частные производные функции F по x ₁, x ₂ и λ, приравняем их к нулю, получим систему уравнений, решив ко которую, получим: λ = -5 000, x ₁ = 2 500, x ₂ = 2 500, L = 12 500 000 руб.

Давая х ₁ значения больше и меньше 2500, находим L и из определения экстремума функции получаем, что L при х ₁ = x ₂ = 2 500 достигает минимума.

Для получения минимальных расходов не­обходимо расходовать в сутки через магазин и торговых аген­тов по 2 500кг муки, при этом расходы на реализацию составят 12 500 000 руб.

Практические занятия.

Используя графический метод, найти глобальные экстремумы функций.

 

1.. L =x 1 + 2 x 2 при ограничениях:	2. L = x 1 + 3 x 2 при ограничениях:
3. L = (x 1 - 6)2 + (x ­2 - 2)2 при ограничениях:	4. L = (x 1 — 3)2 + (x 2 — 4)2 при ограничениях:
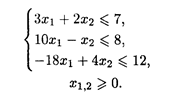
5. L = (x 1 - 4)2 + (x 2 - 3)2 при ограничениях:	6. L = (x 1 - 3)2 + (x 2 — 2)2 при ограничениях:
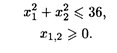
7. L = (x 1 — 2)2 + (x 2 — l)2 при ограничениях:	L = x 12 + x 22 при ограничениях:

Используя метод множителей Лагранжа, найти точку условно­го экстремума

12. L = 2 х 1 х 3 – х 2 х 3 при ограничениях:	13. L = х 1 х 2 + x 2 x 3, при ограничениях:
L =x 1 x 2 + х 2 х 3 при ограничениях:	15. L = 2 x 1 — x 2 + х 3 при ограничениях:

16. Фирма реализует автомобили двумя способами: через розничную и оптовую торговлю. При реализации х ₁ автомоби­лей в розницу расходы на реализацию составляют 4 x ₁ + х ₁² р., а при продаже x ₂ автомобилей оптом — х ₂² р.

Найти оптимальный способ реализации автомобилей, ми­нимизирующий суммарные расходы, если общее число пред­назначенных для продажи автомобилей составляет 200 шт.

 

***

Найти глобальные максимум и минимум дробно-линейных функций.

 

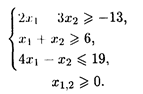
9. L = (2 x 1 - x 2) / (x 1 + x 2) при ограничениях:	10. L = (3 x 1 - x 2)/(x 1 + x 2) при ограничениях:
11. L = (3 x 1 + 7 x 2 )/(x l + х 2 ) при ограничениях: