Тема 2.2. Нелинейное программирование.
1.Общий вид задач нелинейного программирования.
2. Графический метод решения задач нелинейного программирования.
3. Метод множителей Лагранжа.
4. Практические занятия. 1
4.1. Решение задач нелинейного программирования графическим методом.
4.2. Решение задач нелинейного программирования методом множителей Лагранжа.
Общий вид задач нелинейного программирования
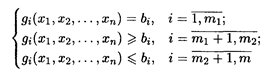Математическая модель задачи нелинейного программирования в общем виде формулируется следующим образом: найти вектор 
= (х 1, x 2, …, xn), удовлетворяющий системе ограничений и доставляющий экстремум (наибольшее или наименьшее значение) целевой функции: L=f(x1,x2,x3,…xn), где xj — переменные, j = 
; L, f, gi — заданные функции от n переменных, bi — фиксированные значения.
В системе ограничений, уравнения и неравенства, а также и целевая функция могут быть сколь угодной сложности.
Нелинейное программирование применяется при прогнозировании промышленного производства, управлении товарными ресурсами, планировании обслуживания и ремонта оборудования и т.д.
Для задачи нелинейного программирования нет единого метода решения.
В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, например, такие как:
| ~ методы множителей Лагранжа, ~ квадратичное и выпуклое программирование, ~ градиентные методы, | ~ приближенные методы решения, ~ графический метод. ~ т.д. |
Из нелинейного программирования наиболее разработаны задачи, в которых система ограничений линейная, а целевая функция нелинейная.
Однако даже для таких задач оптимальное решение может быть найдено для определенного класса целевых функций. В отличие от задач линейного программирования, где точками экстремума являются вершины многогранника решений, в задачах с нелинейной целевой функцией точки могут находиться внутри многогранника, на его ребре или в вершине.
При решении задач нелинейного программирования для целевой функции необходимо определить глобальный максимум или глобальный минимум.
Глобальный максимум функции - наибольшее значение из локальных максимумов.
Глобальный минимум функции - наименьшее значение из локальных минимумов.
Наличие локальных экстремумов затрудняет решение задач, так как большинство существующих методов нелинейного программирования не позволяет установить, является найденный экстремум локальным или глобальным. Поэтому имеется возможность в качестве оптимального решения принять локальный экстремум, который может существенно отличаться от глобального экстремума.
