Графический метод решения задач нелинейного программирования.

Рассмотрим примеры решения задач нелинейного програм­мирования с двумя переменными, причем их целевые функции и системы ограничений могут быть заданы в линейном и не­линейном виде. Так же как и в задачах линейного программи­рования, они могут быть решены графически.

 

2.1. Задача с линейной целевой функцией и нелинейной системой ограничений

Пример 1. Найти глобальные экстремумы..

Целевая функция . Ограничения:

Решение. Область допустимых решений - часть окруж­ности с радиусом 4, которая расположена в первой четверти.

Линиями уровня целевой функции являются параллельные прямые с угловым коэффициентом, равным -2.

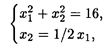Глобальный минимум достигается в точке O (0, 0), глобальный максимум — в точке А касания линии уровня и окружности. Проведем че­рез точку А прямую, перпендикулярную линии уровня.

Прямая проходит через начало координат, имеет угловой коэффициент 1/2 и уравнение x ₂ = 1/2 х ₁.

Решение системы, очевидно:

х ₁ = 8 /5, x ₂ = 4 /5, при этом L = 16 /5 + 4 /5 = 4 .

Ответ. Глобальный минимум, равный нулю, достигается в точке O (0, 0), глобальный максимум, равный 4 , — в точке А (8 /5, 4 /5).

2.2. Задача с нелинейной целевой функцией и линейной системой ограничений

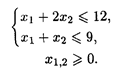
Пример 2. Найти глобальные экстремумы.

Целевая функция 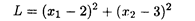Ограничения:

 

Решение. Область допустимых решений – фигура OABD.

Линиями уровня будут окружности с центром в точке O ₁. Максимальное значение целевая функция имеет в точке D (9, 0), минимальное — в точке O ₁ (2, 3). Поэтому

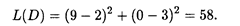
Ответ. Глобальный максимум, равный 58, достигается в точке D (9, 0), глобальный минимум, равный нулю, — в точке O ₁ (2, 3).

Пример 3. Найти глобальные экстремумы:

Целевая функция

Ограничения:

Ращение. Область допустимых решений фигура OABD. Линии уровня представляют собой окружности с центром в точке O ₁ (6, 3).

Глобальный максимум находится в точке О(0,0) как самой удаленной от точки O ₁.

Глобальный минимум расположен в точке Е, находящейся на пересечении прямой 3 x ₁ + 2 x ₂ = 15 и перпендикуляра к этой прямой, про­веденного из точки O ₁.

Найдем координаты точки Е: так как угловой коэффици­ент прямой 3 x ₁ + 2 x ₂ = 15 равен -3/2, то угловой коэффициент перпендикуляра O ₁ Е равен 2/3. Из уравнения прямой, прохо­дящей через данную точку О ₂ с угловым коэффициентом 2/3, получим

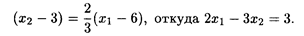
Решая систему находим координаты точки Е: х ₁ = 51/13, x ₂ = 21/13, при этом L(Е) = 1053/169.

Координаты точки Е можно найти и другими способами, например, дифференцируя выражение (x ₁ - 6)² + (x ₂ - 3)² как неявную функцию по x ₁, получим искомые координаты.

Приравниваем полученное значение к тангенсу угла накло­на прямой: 3 x _­1 + 2 x ₂ = 15, откуда получим, что

x₂=-3/2x₁+15/2, tgx=-3/2.

 

Решаем систему уравнений получим координаты точки Е: х ₁ = 51/13, x ₂ = 21/13.

Можно воспользоваться формулой нахождения расстояния от данной точки до данной прямой.

Ответ: Глобальный максимум, равный 52, находится в точке O (0, 0). Глобальный минимум, равный 1053/169, нахо­дится в точке E (51/13, 21/13).

 

2.3.Задача с нелинейной целевой функцией и нелинейной системой ограничений

 

Пример 4. Найти глобальные экстремумы функции

при ограничениях:

 

Решение. Областью допустимых решений является ок­ружность с радиусом 4, расположенная в первой четверти (рис. 28.4). Линиями уровня будут окружности с центром в точке O ₁ (2, l).

Глобальный минимум достигается в точке O ₁. Глобальный максимум — в точке А (0, 4), при этом

Ответ. Глобальный минимум, равный нулю, достигается в точке O ₁ (2, l), глобальный максимум, равный 13, находится в точке А (0, 4).

Пример 5. Найти глобальные экстремумы

Ограничения:

 

Решение. x₁x₂=4 – гипербола x₂=4/x_1.; x₁+x₂=5 – прямая линия x₂=5-x₁

Область допустимых решений не является вы­пуклой и состоит из двух частей. На рисунке эта область представляет собой прямоугольник, без внутренней части, заключенной между гиперболой и прямой линей.

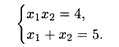Линиями уровня являются окружности с центром в точке O (0, 0).Найдем координаты точек А и В, решая систему

Получим А (1, 4), В (4, 1). В этих точках функция имеет гло­бальные минимумы, равные 17. Найдем координаты точек D и Е, решая системы

Откуда получаем D (2/3, 6) и L(D) = 328/9, E (7, 4/7) и L(E) = 2417/49.

. Ответ. Целевая функция имеет два глобальных миниму­ма, равных 17, в точках А (1, 4) и B (4, 1), глобальный макси­мум, равный 2417/49, достигается в точке E (7, 4/7).