Стегі бар автомат (PDA) – бұл детерминистік емес ақырлы автомат пен жадысы бар лента арқылы құрылған автоматты айтамыз.
Стектің қасиеті:
1) сыйымдылығы шексіз.
2) оқитын тетігі бас жағында орналасады.
3) бос стек λ М= (K, Ʃ, Г, δ,F,S,) мұнда: -K — автомат күйінің ақырлы жиыны; -Σ — алфавитпен есептелінетін мүмкін кіруші алфавиті,мұнда жолдан тілдер формалданады; -S — жад алфавиті;
δ: Q × (Ʃ 
{e}) × (Г 
{λ}) → 
δ(q, a, u) = (P, υ)
NFA: δ(q, a) = P
(P, υ) 
δ(q, a, u) – нені білдіреді?
PDA: М-автоматы q күйінде лентадан а Ʃ өрнек көріп және стектен u Г символын көріп, стектен u символын өшіріп, орнына υ символын жазады және лентаның тетігі оңға бір қадамға көшіп Р күйіне көшеді.
Жағдайлар:
1) υ = λ, (Р, λ)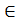 
δ(q, a, u) – стектен өшіру бұйрығы: q а, υ \ λ λ
2) u = λ, (Р, υ) 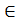δ(q, a, u) – стекке элемент жазу:: q а, λ \ υ Р
3) u = λ, υ = λ, (Р, λ) 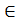δ(q, a, λ) – стекке ешнәрсе істемей NFA-мен жұмыс істеу: q а, λ \ λ Р
Жады стек тәрізді жұмыс атқарады,яғни соңғы жазылған элемент маңызды. Бұдан, өту функциясы бейнесі болып табылады: π: K× Ʃ × S → K × S.
Символды оқиды.Онда негізгі екі амал бар:
Push:Стекке жаңа символ қосу.
Pop: Бас символды оқу және алып тастау
Стек символдарының алфавиті: Γ
Екі ерекше күй бар:бас күй s және соңғы күйлер жиыны F. Ең әуелі,PDA бас күй s-те болады және лента басы ең сол жағында болады, лентада енгізілген сөз бар бірақ, стек бос болады.Лента ең соңғы ұяшыққа келгенде, PDA тоқтайды. Енгізілген сөз x осы PDA-мен қабылданады, егерде PDA соңғы күйге тоқтаса және стек бос болса. Басқа жағдайда сөз қабылданбайды.
PDA-ны төмендегідей сипаттауға болады: M = (Q, Σ, Γ, δ, s, F)
Σ– ену алфавиті, Γ-стектегі символдар алфавиті.
M- PDA арқылы қабылданған барлық сөздердің жиыны L(M).Кейде L(M) тілі M машинасымен қабылданады деп те атаймыз.
PDA үшін транзиттік диаграмма осы PDA-ны сипаттайтын ең тиімді құрал.
M = (Q, Σ, Γ, δ, s, F) үшін,транзиттік диаграмма G=(V, E)түріндегі төмендегі шартты лайық диграф:
V = Q (s =, f =, f Fүшін)
E = { q p | (p,u) δ(q, a, v) }∈a.
16.Ақырлы детерминистік автоматты формалды түрде сипатта. Не себепті автомат ақырлы деп аталады? Ақырлы детерминистік автоматта жадысы бар ма? Ақырлы детерминистік автомат деп(DFA)- M=<K，Σ，δ，S, F>, бестігін айтамыз. Мұндағы: К – күйлер жиыны (ақырлы), Σ – алфавит, S∈К – бастапқы күй, F⊆К – ақырлы күйлер, δ – көшу функциясы. δ функциясы К×Ʃ→К. Кез келген q∈Q, a∈Σ үшін δ(q,a)-нақтылы анықталған мәні бар болса, онда ондай автоматты Детерминистік ақырлы автомат деп атаймыз. Ереже бойынша, М автоматының келесі күйі өту функциясында кодталған. Бұдан, егер М q∈К күйінде болып, лентадан a∈Σ символы оқылса, онда автоматтың өтетін жалғыз анықталатын күйі, ол δ(q,a) ∈К. Детерминистік ақырлы автомат кіріс сөзінің оқылған бөлігіне басын қайтадан артқа бұрай алмайды, сол жақ бөлігіндегі сөз саналатын басындағы машинаның ары қарай функциялануына әсер ете алмайды. Детерминистік автоматтың конфигурациясы <K，Σ，δ，S, F> - бұл К× 
кез-келген элемент. Ақырлы автомат детерминистік деп аталады егер: 1)множество I дәл 1 ғана элементтен тұрса, 2)әрбір <p, x, q> ∈ Δ өтуі үшін |x| = 1 теңдігі орындалса. 3)кез-келген a ∈ Σ символы және p ∈ Q күйі үшін, < p, a, q>∈ Δ құрылымды бір q ∈ Q күйі болады. M- қабылданатын тіл: ∀x∈Σ* үшін, егер δ(q,w)∈F болса, онда x-ті M-қабылдайды дейміз, ал δ(q,w) ∉F болса, онда M-автоматы x-ті қабылдамайды деп атаймыз. L(M)={x| x∈Σ* әрі δ(q,w)∈F } M-автоматымен қабылданатын тіл: L(M1)= L(M2)={02n|n≥1} Егер L(M1)=L(M2), онда M1мен M2 автоматтары эквивалент деп аталады. Мысал: M=<K，Σ，δ，S, F>, К={q0, q1}, Ʃ={a,b}, S=q0, F={q0}
δ – функциясы келесі кестемен өрнектеледі:
17) Ақырлы детерминистік автомат пен детерминистік емес автоматтын арасындағы айырмашылықтарын сипатта.
Аықырлы автомат (finite automaton,FA) M=(Q，Σ，δ，q0，F) Q——күйлердің бос емес
ақырлы жиыны. ∀q∈Q，q-ді M-ның бір күйі деп атаймыз. (state). Σ—— алфавит (Input alphabet).
Енгізілген сөздер тізбегі тек Σ дағы cимволдардан алынады. q0——q0∈Q, M-автоматының бастапқы күйі (initial state).δ——күй ауыстыру функциясы (transition function). δ：Q×Σ→Q, ∀(q，a)∈Q×Σ，үшін δ(q，a)=p арқылы ：M-автоматының q күйінле тұрып a символын оқып, күйін p-ға ауыстыруды сонымен бірге оңға қарай бір қадам жылжыуды білдіреді. F——F⊆Q, M-ның аяқтау күйлерінің жиынын білдіреді (final state). ∀q∈F, q-ді M-ның тоқтау күйі деп атаймыз немесе қабылдау күйі (accept state).Кез келген q∈Q, a∈Σ үшін δ(q,a)-нақытылы анықтаған мәні бар болса, онда ондай автоматтыДетерминистік ақырлы автомат деп атаймыз.
M- қабылдайтін тіл: ∀x∈Σ*үшін,егер δ(q,w)∈F болса, онда x-ті M-қабылдайды дейміз, ал δ(q,w) ∉F болса, онда M-автоматы x-ті қабылдамайды деп атаймыз. L(M)={x| x∈Σ*әрі δ(q,w)∈F }
M-автоматымен қабылданатын тіл. -L(M1)= L(M2)={02n|n≥1} Егер L(M1)=L(M2), онда M1мен M2 автоматтары эквивалент деп аталады.
Ақырлы детерминистік емес автомат бұл- 
дегеніміз ақырлы күйдін жиыны. 
алфавит 
бастапқы күй
ақырлы күйдін жиыны 
көшу қатынасы,ішкіжиыны 
Орналасқан a және жетекші 
М күй диаграммасында. Егер М 
күйінде орналасса, онда а келесі оқылатын символ болып табылады, сонымен М ары қарай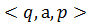 
күйлеріне түріне немесе 
: егер 
оқытын болса онда символ оқылмайды.
Формалды түрде есептелінетін ақырлы детерминистік емес автомат, детерминистік автоматка өте ұқсас.
Детерминистік емес ақырлы автоматтардан бірнеше күй шығаруға болады.
