Бинар қатынастардың негізгі түрлері. Рефлексив және транзитив тұйықтау.
Бинарлық қатынас деп екі объектінің арасындағы қатынасты айтады. Бинарлық қатынасты реттелген жұптардың жиынтығы ретінде аныктауға болады. Мысалы. егер бізді нақты а және в жеке тұлғаларының арасындағы «сыйластық» қатынасы қызыктырса, онда мұндай қатынастардың түрі әртүрлі болуы мүмкін. Сонымен, R = {(a,b)} қатынасы а-ның b -ның сыйлайтындығын білдіреді. R} = {(a,b), (а, а)} қатынасы а-ның в -ны сыйлайтындығын және в –ның а -ны сыйлайтындығын білдіреді. Бізді кызыктырып отырған тұлғалардың арасындағы «сыйластық х қатынасының басқа да түрлерін анықтауға болады: R2={(a,b){a,a)}, R3= {{a,a){b.b)}, т.с.с.
Анықтама. Бос емес  жиындары берiлсiн. Онда реттелген элементтер жиыны
жиындары берiлсiн. Онда реттелген элементтер жиыны
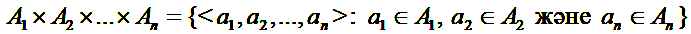 жиыны
жиыны  жиындарының декарттықкөбейтiндiсi деп аталады. Олардың элементтерiн n-дiктер деп атаймыз. Жалпы жағдайда бұл көбейтінді кезкелген I индекстік жиыны үшін бұл көбейтiндi
жиындарының декарттықкөбейтiндiсi деп аталады. Олардың элементтерiн n-дiктер деп атаймыз. Жалпы жағдайда бұл көбейтінді кезкелген I индекстік жиыны үшін бұл көбейтiндi  түрiнде жазылады. Мұндағы I жиыны ақырсыз жиын болуыда мүмкiн
түрiнде жазылады. Мұндағы I жиыны ақырсыз жиын болуыда мүмкiн
Ал  арқылы А жиынын өзiне өзiн n рет көбейткеннен пайда. Болған жиын белгіленеді. Олжиын А жиынының n-шi дəрежес деп аталады..
арқылы А жиынын өзiне өзiн n рет көбейткеннен пайда. Болған жиын белгіленеді. Олжиын А жиынының n-шi дəрежес деп аталады..
Анықтама. Бос емес А жиыны берiлсiн. Мұндеғы n – оң бүтiн сан, онда An
жиынының кез келген iшкi жиынын А жиынында анықталған n-орынды қатынас деп атаймыз.1-орынды қатынастар унарлық, 2- орынды қатынастар бинарлық, 3-орындықатынастар тернарлық қатынастар деп аталады. Практикада негiзiнен унарлық жəне бинарлық қатынастармен жұмыс iстеймiз. Əсiресе, төменде келтiрiлетiн арнайы бинарлық қатынастар математикада кеңінен жəне табысты қолданылады. Осы бөлімде R арқылы А жиынында анықталған бинарлық қатынасты белгiлеуге келіселік. Сонымен бірге, (a,b) парының R қатынасына тиістілігін (а,b)ÎR немесе aRb Бiздiң курсымызда ерекше маңызды жəне жиi кездесетiн арнайы бинарлық қатынастарды анықтаймыз.
1. Егер кез келген xÎA элементi үшiн (x,x)ÎR болса, онда R қатынасы Рефлексивтi қатынас деп аталады.
2. Егер кез келген x, y, zÎA элементтерi үшiн (x, y)ÎR жəне (y, z)ÎR 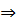 (x, z)ÎR шарты орындалса, онда R қатынасы транзитивтi деп аталады.
(x, z)ÎR шарты орындалса, онда R қатынасы транзитивтi деп аталады.
Жиындарға қолданылатын амалдар. Функциялар және қатынастар
Саналымды және санаусыз жиындар.
Жиын ретiнде оның қандай да бiр белгiлерiн ескеріп, әртүрлi объектiлердiң алдын - ала берiлген ерекшелiктерi бойынша топтастырылуын айтамыз Жиындарды үлкен латын әрiптерi арқылы белгiлеймiз: A, B, X, P, T және т.б. Жиынды құрайтын нысандар осы жиынның элементтерi деп аталады. Жиын элементтерi кiшi латын әрiптерiмен белгiленедi: a, b, c, x, u, v және т. б. Қажет болған жағдайда, тӛменгi немесе жоғарғы индекстер еркiн қолданылады. Жиындарды олардың элементтерiнiң тiзiмiн немесе олардың элементерiне ортақ қасиеттердi кӛрсету жолымен беруге болады Ақырсыз жиындар негізінен екінші тәртiппен анықталады. Бiздiң келешек баяндауларымыз үшiн тӛмендегi сандық жиындар кеңiнен қолданылады. натурал сандар жиыны, бүтiн сандар жиыны  рационал сандар жиыны, R нақты сандар жиыны. Бұл жиын рационал және иррационал сандардың бірігуінен тұрады. Жиындар арасындағы байланыстар – жиындарға қолданылатын тӛмендегi амалдарды анықтайды.
рационал сандар жиыны, R нақты сандар жиыны. Бұл жиын рационал және иррационал сандардың бірігуінен тұрады. Жиындар арасындағы байланыстар – жиындарға қолданылатын тӛмендегi амалдарды анықтайды.
Егер А жиынының барлық элементтерi B жиынына тиiстi болса, онда А жиынын
B жиынының iшкi жиыны деп атаймыз. Ал B жиыны А жиынын қамтушы жиын
деп аталады.Ешбiр элементi болмайтын жиынды бос жиын деп атаймыз. – бос жиын
белгiсi. Анықтауымыз бойынша бос жиын кез келген жиынның ішкі жиыны болады.
Кез келген A,B,C жиындары үшін:⑴ A=B ⇔ A⊆B және B⊆A. ⑵ егер A⊆B,онда |A|≤|B|. егер A⊂B,онда |A|≤|B| ⑶ Егер A ақырлы жиын болса әрі A⊂B онда |B|>|A|⑸ Егер A⊆B, онда∀x∈A үшін x∈B. ⑹ ЕгерA⊂B, онда ∀x∈A үшін x∈B және ∃x∈B бірақ x∉A. ⑺ Егер A⊆B және B⊆C онда A⊆C. ⑻ Егер A⊂B және B⊂C сонымен бірге не A⊆Bәрі B⊂C не A⊂Bәрі B⊆C бірі орындалса онда A⊂C. ⑼ егер A=B болса, онда |A|=|B|.
Егер Т⊆W және табылады x∈W болса, бірақ х∉Т орындалса, T жиынын W жиынының меншiктi iшкi жиыны деп атаймыз.
1. А және В жиындарына ортақ элементтерден ғана тұратын жиынды А және В жиындарының қиылысуы деп атап, ол жиынды А ∩ В арқылы белгiлеймiз. Егер А ∩ В = ᴓболса, онда А және В жиындарын қиылыспайтын жиындар деп атаймыз. ⑴ A∩B= B∩A.⑵ (A∩B)∩C=A∩(B∩C). ⑶ A∩A=A ⑷ A∩B=A ⇔ A⊇B. ⑸ Φ ∩A= Φ. ⑹ |A∩B|≤min{|A|,|B|}. ⑺ A∩(B∪C)=(A∩B)∪(A∩C). ⑻ A∪(B∩C)=(A∪B)∩(A∪C). ⑼ A∩(A∪B)=A.
⑽ A∪(A∩B)=A.
2. А және В жиындарының ең болмағанда бiреуiне тиiстi элементтерден тұратын
жиынды – А және В жиындарының бiрiгуi деп атаймыз. Оны А Ụ В таңбасы арқылы белгiлеймiз.
 A1∪A2∪…∪An={a|∃i1≤i≤n,a∈Ai}
A1∪A2∪…∪An={a|∃i1≤i≤n,a∈Ai}
3. А жиынына тиiстi, ал В жиынына тиiстi емес элементтерден тұратын жиын А
жиыны мен В жиынының айырмасы (А минус В) деп аталып, А \ В арқылы
белгiленедi. ⑴ A-A= Φ
⑵ A- Φ =A ⑶ A-B ≠ B-A ⑷ A-B=A iff A∩B= Φ\
⑸ A∩(B-C)=(A∩B)-(A∩C) ⑹ |A-B|≤|A|
4. Симметриялық айырма (symmetric difference):A  ∪(B\A)
∪(B\A)
Ал А жиынына тиiстi емес және А жиынын қамтушы қандай да бiр жиынның элементтерiнен тұратын жиынды А жиынының аталған қамтушы жиындағы толықтаушы жиыны деп атаймыз. Белгiлеуi: 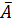
 Бұл суреттегi боялған бӛлiк, А
Бұл суреттегi боялған бӛлiк, А
жиынының толықтаушы жиыны – A жиынын бiлдiредi. 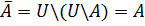 - конволюция заңы.
- конволюция заңы.
Элементтерiнiң саны белгiлi бiр натурал санға тең болатын жиынды ақырлы
жиын деп атаймыз. Ақырлы жиынның элементтер санын оның қуаты деп атайды.
Сонымен бірге, ақырлы жиын деп, ӛзiнiң кез келген меншiктi iшкi жиынымен ӛзара әрмәндi сәйкестiкте болмайтын жиынды айтуға болатыны төменде кӛрсетіледі. Ал мұндай сәйкестiктер табылатын жиынды ақырсыз жиын деймiз.
Анықтама. Бос емес А1, А2,...,А n жиындары берiлсiн. Онда реттелген элементтер жиыны 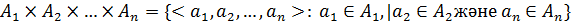
жиыны А1, А2,...,А n жиындарының декарттық көбейтiндiсi деп аталады.
Олардың элементтерiн n-дiктер деп атаймыз.
Анықтама. Бос емес А жиыны берiлсiн. Мұндеғы n – оң бүтiн сан, онда n
жиынының кез келген iшкi жиынын А жиынында анықталған n-орынды қатынас
деп атаймыз.1-орынды қатынастар унарлық, 2-орынды қатынастар бинарлық, 3-орынды
қатынастар тернарлық қатынастар деп аталады
1. Егер кез келген x € A элементi үшiн (x, x) € R болса, онда R қатынасы рефлексивтi қатынас деп аталады.
2. Егер кез келген x, y € A элементтерi үшiн (x, y)€ R ó (y, x) € R шарты орындалса, онда R қатынасы симметриялы деп аталады.
3. Егер кез келген x, y, z € A элементтерi үшiн (x, y) € R және (y, z) € R => (x, z) € R шарты орындалса, онда R қатынасы транзитивтi деп аталады.
4. Кез келген x € A үшiн (x, x)тиісті емес R болса, онда R қатынасы иррефлексивтi деп
аталады.
5. Кез келген x, y € A үшiн (x, y)€ R және (y, x) € R болғандығынан x = y теңдiгi
орындалса, онда R қатынасы антисимметриялы деп аталады.
A жиынында анықталған рефлексивтi, симметриялы және
транзитивтi қатынас эквиваленттiлiк қатынас деп аталады. Функциялар Егер төмендегі шарттар орындалса, онда f 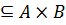 қатынасын функция деп атайды
қатынасын функция деп атайды
dom f=A
Im f ⊆B
(x, 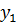 )
) 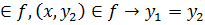
Dom f - функцияның анықталу аймағы, ал Im f - функцияның мәндер аймағы. Сонымен, функция бинарлық қатынас болады.
f:A  B
B
функциясын инъекция деп атайды, егер кез келген 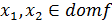 үшін x1!=x2 теңсіздігінен f(x1)!= f(x2) теңсіздігі шықса.
үшін x1!=x2 теңсіздігінен f(x1)!= f(x2) теңсіздігі шықса.
f:A  B
B
функциясын сюръекция деп атайды, егер Im f=B теңдігі орындалса.
Егер f:A  B
B
функциясы инъекция және сюръекция болса, онда оны биекция деп атайды.
f:R  R,
R, 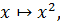 инъекция да, сюръекция да емес
инъекция да, сюръекция да емес
f:R 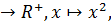 сюръекция, бірақ инъекция емес
сюръекция, бірақ инъекция емес
f:Z 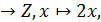 инъекция, бірақ сюръекция емес
инъекция, бірақ сюръекция емес
f:R  ,биекция.
,биекция.




