Σ -алфабиті бойынша регуляр өрнек келесідей рекурсивті жолмен анықталады: 0-регуляр өрнек болып табылады; 1- регуляр өрнек болып табылады; егер 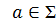 болса, онда
болса, онда 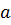 -регуляр өрнек болады; егер
-регуляр өрнек болады; егер 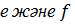 регуляр өрнек болса, онда (
регуляр өрнек болса, онда (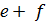 ), (
), (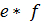 ) және
) және 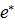 өрнектері де регуляр өрнектер болады.
өрнектері де регуляр өрнектер болады.
Жақшаларды азайту мақсатында, 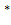 операциясының приоритеті көбейту операциясынан жоғары, ал көбейту амалының приоритеті қосу операциясына қарағанда жоғары деп аламыз. Көбінесе
операциясының приоритеті көбейту операциясынан жоғары, ал көбейту амалының приоритеті қосу операциясына қарағанда жоғары деп аламыз. Көбінесе 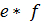 -тің орнына
-тің орнына 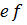 деп жазады.
деп жазады.
Мысалы: 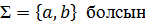 . Онда
. Онда 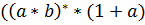 –регуляр өрнек болады.
–регуляр өрнек болады.
Әрбір е регуляр өрнегі  алфабиті бойынша қандай да бір тіл құрады, ол келесідей рекурсивті жболмен анықталады:
алфабиті бойынша қандай да бір тіл құрады, ол келесідей рекурсивті жболмен анықталады:
1) L(a)⇔{a}, егер 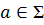 болса,
болса,
2) L(0)⇔ø,
3) L(1)⇔{e},
4) L(e*f)⇔ 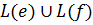 ,
,
5) 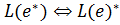
АН: L- регуляр тіл деп аталады, егер ол қандай да бір регуляр өрнекпен анықталса.
Ан: е-регуляр өрнек болсын. Онда
1)  2)
2) 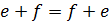 3) e+0=e 4)
3) e+0=e 4) 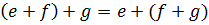
5) 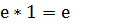 6)
6) 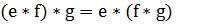 8)
8) 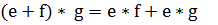 9)
9) 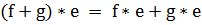
10) 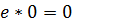 11)
11) 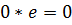
Лемма: Кез-келген 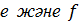 регуляр өрнектері үшін келесі тепе-теңдіктер орындалады:
регуляр өрнектері үшін келесі тепе-теңдіктер орындалады:
1) 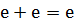
2) 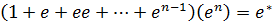
3) 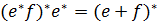
4) 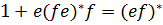
Лемма: Кез-келген 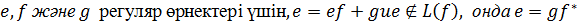
L тілі регулярлы тіл деп аталады, егерде М автоматы табылып: 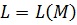 орындалса. Ақырлы автоматпен қабылданатынбарлық тіл регулярлы.
орындалса. Ақырлы автоматпен қабылданатынбарлық тіл регулярлы.
5. Детерменистік ақырлы автоматтар, олармен қабылданатын тілдер. Конфигурация.Детерминистік автоматпен қабылданатын тіл. Ақырлы автомат (finite automaton,FA) M=(Q,Σ,δ,q0,F) Q——күйлердің бос емес ақырлы жиыны. ∀q∈Q,q-ді M-ның бір күйі деп атаймыз. (state). Σ—— алфавит (Input alphabet). Енгізілген сөздер тізбегі тек Σ дағы cимволдардан алынады. q0——q0∈Q, M-автоматының бастапқы күйі (initial state). δ——күй ауыстыру функциясы (transition function). δ:Q×Σ→Q, ∀(q,a)∈Q×Σ,үшін δ(q,a)=p арқылы :M-автоматының q күйінде тұрып a символын оқып, күйін p-ға ауыстыруды сонымен бірге оңға қарай бір қадам жылжытуды білдіреді. F——F⊆Q, M-ның аяқтау күйлерінің жиынын білдіреді (final state). ∀q∈F, q-ді M-ның тоқтау күйі деп атаймыз немесе қабылдау күйі (accept state). Анықтама: Конфигурация немесе тез бейнелеу(instantaneous description) ақырлы автоматы (Q, Σ, ∆, I, F) деп кез-келген реттелген жұпты (q,  ) айтамыз, мұнда q∈Q және
) айтамыз, мұнда q∈Q және  ∈
∈  .
.
Анықтама: Барлық конфигурацияның көбіндегі ақырлы автоматын М бинарлық қатынасты  келесідей анықтаймыз. Егер (p, x, q) ∈∆ және
келесідей анықтаймыз. Егер (p, x, q) ∈∆ және  ∈
∈  , онда (p, x
, онда (p, x  )
) 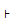 (q, w)
(q, w)
δ ны толықтыру: 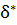 : Q×
: Q× 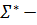 > Q. Кез-келген q∈Q
> Q. Кез-келген q∈Q  ∈
∈ 
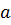 ∈
∈  үшін (1)
үшін (1) 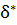 (q,
(q,  )= q (2)
)= q (2) 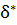 (q,
(q, 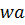 )= δ (
)= δ (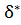 (q,
(q, 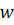 ), a)
), a) 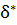 (q,
(q, 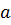 )=
)= 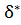 (q,
(q, 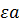 )= δ (
)= δ (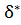 (q,
(q, 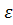 ), a) = δ(q,
), a) = δ(q, 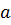 ) Кез келген q∈Q, a∈Σ үшін δ(q,a)-нақтылы анықтаған мәні бар болса, онда ондай автоматты Детерминистік ақырлы автомат деп атаймыз M- қабылдайтыаан тіл: ∀x∈Σ*үшін,егер δ(q,w)∈F болса, онда x-ті M-қабылдайды дейміз, ал δ(q,w) ∉F болса, онда M-автоматы x-ті қабылдамайды деп атаймыз. L(M)={x| x∈Σ*әрі δ(q,w)∈F } M-автоматымен қабылданатын тіл. -L(M1)=L(M2)={02n|n≥1} Егер L(M1)=L(M2), онда M1мен M2 автоматтары эквивалент деп аталады. Егер q ден
) Кез келген q∈Q, a∈Σ үшін δ(q,a)-нақтылы анықтаған мәні бар болса, онда ондай автоматты Детерминистік ақырлы автомат деп атаймыз M- қабылдайтыаан тіл: ∀x∈Σ*үшін,егер δ(q,w)∈F болса, онда x-ті M-қабылдайды дейміз, ал δ(q,w) ∉F болса, онда M-автоматы x-ті қабылдамайды деп атаймыз. L(M)={x| x∈Σ*әрі δ(q,w)∈F } M-автоматымен қабылданатын тіл. -L(M1)=L(M2)={02n|n≥1} Егер L(M1)=L(M2), онда M1мен M2 автоматтары эквивалент деп аталады. Егер q ден  қа дейін w арқылы жол бар болса, онда оны төмендегідей белгілейміз
қа дейін w арқылы жол бар болса, онда оны төмендегідей белгілейміз 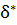 (q,
(q, 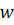 ) =
) = 
6.Ақырлы детерминистік емес автомат ұғымы. Детерминистік емес автоматпен қабылданатын тіл. Детерминистік емес ақырлы автомат - бұл мына бестіктен тұрады:М=(K, Σ, ∆, s, F) K- ақырлы күйлердің жиыны Σ- алфавит s∈K- бастапқы күй F 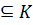 - ақырлы күйлер жиыны ∆- көшу күйі, K×(Σ
- ақырлы күйлер жиыны ∆- көшу күйі, K×(Σ 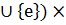 K Анықтама: Конфигурация немесе тез бейнелеу(instantaneous description) ақырлы автоматы (Q, Σ, ∆, I, F) деп кез-келген реттелген жұпты (q,
K Анықтама: Конфигурация немесе тез бейнелеу(instantaneous description) ақырлы автоматы (Q, Σ, ∆, I, F) деп кез-келген реттелген жұпты (q,  ) айтамыз, мұнда q∈Q және
) айтамыз, мұнда q∈Q және  ∈
∈  . Ламбда тасымалы
. Ламбда тасымалы 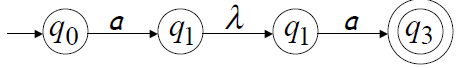
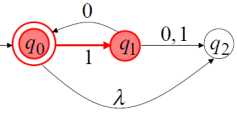
Орындалады сонда және тек қана сонда егер qi-ден qj -ге дейін w бойынша бір жол
бар болса болады
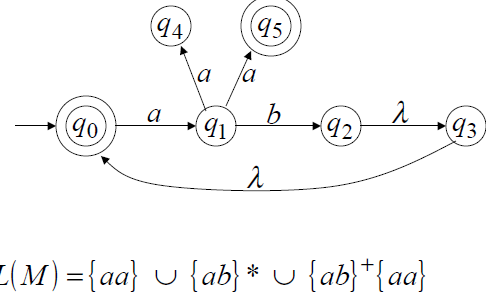


Әр үштік (q, u, p) ∈∆ М ге көшу деп аталады; Бұл бағыттың формализациясы. Анықталынған детерменистік ақырлы автоматтармен детерменистік емес ақырлы автоматты есептеудiң анықтамасы өте ұқсас. Конфигурация М бұл K× 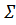 . Конфигурацияның арасындағы жағдай
. Конфигурацияның арасындағы жағдай 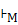 былай анықталады: (q, w)
былай анықталады: (q, w) 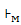 (
(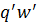 ) сонда және тек сонда ғана, u∈
) сонда және тек сонда ғана, u∈ 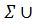 {e} болған жағдайда, w=u
{e} болған жағдайда, w=u 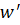 және (q, u,
және (q, u,  ) ∈∆. Байқасақ
) ∈∆. Байқасақ 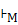 – міндетті түрде функция емес: кейбір конфигурацияларға (q, w) бірнеше жұп болуы мүмкін (
– міндетті түрде функция емес: кейбір конфигурацияларға (q, w) бірнеше жұп болуы мүмкін (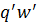 ) немесе ешқандай жұп болмауы мүмкін - (q, w)
) немесе ешқандай жұп болмауы мүмкін - (q, w) 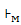 (
(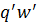 ).
).
7. Детерминистік емес автоматтар мен детерминистік автоматтардың
Эквиваленттілігі.
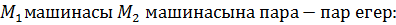
L( )=L(
)=L(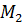 )
)
NFA=DFA?
{NFA қабылдайтын тіл} = {DFA қабылдайтын тіл} Дәлелдейміз: NFA және DFA да бірдей есептеу күші бар 1 КАДАМ: {NFA қабылдайтын тіл} 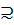 {DFA қабылдайтын тіл}
{DFA қабылдайтын тіл}
Дәлел: әрбір DFA-NFA болады, DFA қабылдайтын тілді NFA қабылдайды.
2 ҚАДАМ: {NFA қабылдайтын тіл} ⊆ {DFA қабылдайтын тіл}
Дәлел: кез келген NFA-ны сәйкес пара-пар DFA-ға аударуға болады. NFA қабылдаған тілді DFA қабылдайды.
NFA-дан DFA-ға





