ычислительный блок Given/Find

абораторная работа №2.

екторная алгебра. аналитическая геометрия.

Цель работы: выполнение действий с векторами и нахождение решений задач аналитической геометрии в программе MathCad.

 

Указания к выполнению лабораторной работы:

І. Запустить программу MathCad.

ІІ. Написать разложение вектора по векторам _{, ,} .

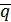ІІІ. Найти косинус угла между векторам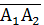и . и .

ІV. Вычислить объем тетраэдра с вершинам1и в точках A₁, A₂, A₃, A₄ и его высоту, опущенную из вершины A₄ на грань A₁A₂A₃.

V. Найти угол между плоскостями

VI Написать канонические уравнения прямой.

VII. Найти точку M¢, симметричную точке M относительно прямой (для вариантов 1-15) или плоскости (для вариантов 16-31).

MATHCAD

 

Векторная алгебра

Векторы являются частным случаем матриц размерности N×1, поэтому для них справедливы все операции, что и для матриц, если ограничения особо не оговорены. Вместе с тем для векторов в линейной алгебре предусмотрен целый ряд специфических операций, и все они реализованы в системе Mathcad. Непосредственное проведение многих векторных операций над матрицами-строками, т.е. матрицами размерности 1×N, невозможно; для того, чтобы превратить строку в вектор, ее нужно предварительно транспонировать.

Модуль вектора по определению равен квадратному корню из суммы квадратов его элементов (листинг 1).

Листинг 1. Модуль вектора

 

Не путайте модуль вектора и определитель матрицы, который обозначается тем же символом. Это характерный пример оператора, действующего по-разному на векторы и квадратные матрицы.

 

Скалярное произведение векторов определяется как скаляр, равный сумме попарных произведений соответствующих координат. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность. Скалярное произведение двух векторов 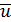и равно

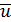· =| | | COSθ, где θ – угол между векторами. Если векторы ортогональны, то их скалярное произведение равно нулю. Обозначается скалярное произведение тем же символом, что и умножение (листинг 2).

 

Листинг 2. Скалярное произведение векторов

 

 

Для обозначения скалярного произведения пользователю позволяется выбирать представление оператора умножения при помощи контекстного меню (подобно умножению скалярных величин). Однако никогда не применяйте для обозначения скалярного произведения символ ×, который является общеупотребительным символом векторного произведения.

 

 

Листинг 3. Скалярное произведение векторов,умноженное на третий вектор

 

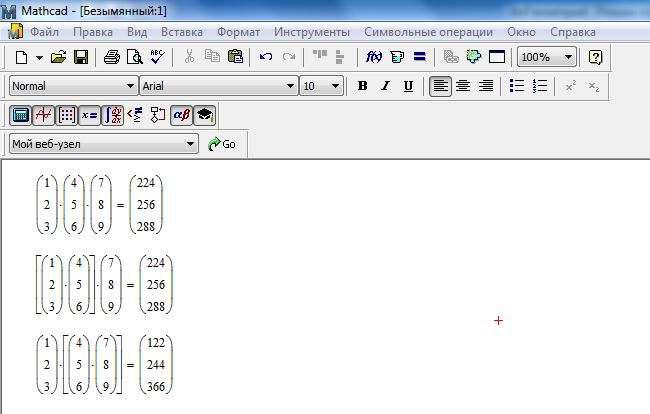
С осторожностью перемножайте несколько (более двух) векторов.

По-разному расставленные скобки полностью изменяют результат умножения. Примеры такого умножения приведены в листинге 3.

Векторное произведение двух векторов 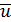и с углом θ между ними равно

равно вектору с модулем 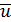· =| | | sinθ, направленным перпендикулярно плоскости векторов u и v. Обозначают векторное произведение символом ×, который можно ввести нажатием кнопки Cross Product (Векторное произведение) в панели Matrix (Матрица) или сочетание клавиш <Ctrl>+<8>. Пример приведен в листинге 4.

 

Листинг 4. Векторное произведение двух векторов

 

 

Векторная алгебра Mathcad включает несколько необычный оператор, который называется оператором векторизации. Этот оператор предназначен, как правило, для работы с массивами. Он позволяет провести однотипную операцию над всеми элементами массива (т.е. матрицы или вектора), упрощая тем самым программирование циклов. Например, иногда требуется умножить каждый элемент одного вектора на соответствующий элемент другого вектора, чтобы в результате также получился вектор. Непосредственно такой операции в Mathcad нет, но ее легко осуществить с помощью векторизации (листинг 5). Для этого:

 

1. Введите векторное выражение, как показано во второй строчке листинга 5 (обратите внимание, что в таком виде символ умножения обозначает оператор скалярного произведения векторов).

 

2. Переместите курсор таким образом, чтобы линии ввода выделяли все выражение, которое требуется подвергнуть векторизации.

 

3. Введите оператор векторизации, нажав кнопку Vectirize (Векторизация) на панели Matrix (Матрица) (листинг 5), или сочетанием клавиш

 

<Ctrl>+<_>.

4. Введите <=>, чтобы получить результат.

 

Листинг 5. Использование оператора векторизации для перемноженияэлементов вектора

 

Большинство неспецифических функций Mathcad не требуют векторизации для проведения одной и той же операции над всеми элементами вектора. Например, аргументом тригонометрических функций по определению является скаляр. Если попытаться вычислить экспоненту от векторной величины, Mathcad осуществит векторизацию по умолчанию, возведя в степень e каждый элемент и выдав в качестве результата соответствующий вектор (листинг 6).

 

Листинг 6. Векторизация аргумента необязательна для большинствавстроенных функций Mathcad

 

Слияние матриц

 

Для того чтобы составить из двух или более матриц одну, в Mathcad предусмотрена пара матричных функций (листинг 7):

 

- augment(A,B,C,…) – матрица, сформированная слиянием матриц-аргументов слева направо;

 

- stack(A,B,C,…) – матрица, сформированная слиянием матриц-аргументов сверху вниз;

 

A,B,C,…. – векторы или матрицы соответствующего размера.

 

Листинг 7. Примеры слияния матриц

 

Вычисление коэффициентов полинома

 

Если выражение является полиномом относительно некоторой переменной x, заданным не в обычном виде a₀ + a₁x + a₂x² +...., а как

 

произведение других, более простых полиномов, то коэффициенты a₀,a₁,a₂,... легко определяются символьным процессором Mathcad.

 

Коэффициенты сами могут быть функциями (подчас довольно сложными) других переменных. Чтобы вычислить полиномиальные коэффициенты в выражении при помощи меню:

 

1. Введите выражение.

 

2. Выделите в нем имя переменной или выражение, для которого требуется рассчитать полиномиальные коэффициенты.

 

3. Выполните команду Symbolic/Polynomial Coefficients (Символика/

Коэффициенты полинома).

 

В результате под выражением появится вектор, состоящий из полиномиальных коэффициентов. Первым элементом вектора является

 

свободный член a₀, вторым – a₁ и т.д.

 

Чтобы вычислить полиномиальные коэффициенты с помощью оператора символьного вывода:

 

1. Введите выражение.

2. Нажмите кнопку Coeffs на панели Symbolic (Символика).

3. Введите в местозаполнитель после вставленного ключевого слова coeffs аргумент полинома.

 

4. Введите оператор символьного вывода ®.

5. Нажмите клавишу <Enter>/

 

Листинг 8. Вычисление коэффициентов полинома

 

Листинг 9. Вычисление полиномиальных коэффициентов для простойпеременной из выражения

 

 

Примеры вычисления коэффициентов полинома приведены в листингах 8 и 9. Листинг 8 показывает расчет коэффициентов для разных аргументов. Листинг 9 демонстрирует возможность определения коэффициентов не только для отдельных переменных, но и для более сложных выражений, входящих в рассматриваемую формулу в качестве составной части.

 

Явные вычисления

 

В Mathcad 13 появилась возможность осуществления явных символьных вычислений. Этим термином разработчики обозначили расчеты, в которых осуществляется простая подстановка в выражение численного значения той или иной переменной (без упрощения результата). Для организации явных вычислений предусмотрено специальное ключевое слово explicit, которое вводится с панели Symbolic (Символика). Сама формула вводится в левый местозаполнитель, а переменные, числовые значения которых должны быть подставлены в нее явно и без упрощения – в правый местозаполнитель. Пример вычислений, включающих ключевое слово explicit, приведен в листинге 10.

 

 

Листинг 10. Явные вычисления

 

Подстановка переменной

 

Очень удобная возможность символьных вычислений – это операция подстановки значения переменной в выражение. При помощи меню

 

подстановка производится следующим образом (рис.1):

1. Выделите значение переменной, которое необходимо подставить в некоторое выражение. Значение переменной может быть любым выражением относительно любых переменных (на рис. 1 в качестве подстановки взята самая первая строка документа).

2. Скопируйте значение переменной в буфер обмена, например, нажатием клавиш <Ctrl>+<C> или кнопки Copy (Копировать) на панели инструментов Standard (Стандартная).

 

3. Выделите в выражении, в которое требуется подставить значение из буфера обмена, переменную, которая будет заменяться (во второй строке на рис. 1 выделена переменная x).

 

4. Выполните команду Symbolics / Variable / Substitute (Символика /

 

Переменная /Подставить).

Результат этих действий иллюстрируется нижней строкой в документе на рис. 1.

 

 

Рис. 1. Подстановка значения переменной

 

Листинг 11. Подстановка значения переменной

 

Для осуществления той же операции в совокупности с оператором символьного вывода используйте ключевое слово substitute, которое

 

вставляется в документ одноименной кнопкой на панели Symbolic (Символика). После ключевого слова substitute необходимо ввести в

 

местозаполнители логическое выражение, показывающее, какую именно переменную, какой формулой следует заменить (листинг 11).

 

ычислительный блок Given/Find

 

Рассмотрим решение системы n нелинейных уравнений с m неизвестными:

 

 

Здесь f1(x1,...,xm) = b1,…,	fn (x1,...,xm) = bn	– некоторые скалярные
выражения, зависящие от скалярных переменных	x1,...,xm и, возможно, от

еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему (1) можно формально переписать в виде

 

f(x) = b,	(2)
где x – вектор, составленный из переменных	x1,...,xm; b – вектор,
составленный из правых частей уравнений, а	f(x) – соответствующая
векторная функция их левых частей.

 

Листинг 12. Аналитическое решение кубических уравнений

 

 

Для решения систем в Mathcad применяется специальный вычислительный блок Given/Find (Дано/ Найти), состоящий из трех частей, идущих последовательно друг за другом:

 

· Given – ключевое слово;

· Система, записанная логическими операторами в виде равенств и, возможно, неравенств;

 

· Find (x₁,...,x_m) – встроенная функция для решения системы уравнений

относительно переменных x₁,...,x_m.

Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Если вы предпочитаете ввод с клавиатуры, помните, что логический знак равенства вводится сочетанием клавиш <Ctrl>+<=>. Значение функции Find представляет собой матрицу, составленную из всевозможных решений по каждой переменной, причем количество ее строк в точности равно числу аргументов Find. Структура матрицы решения приведена в следующих листингах.

 

Листинг 13. Символьное решение системы двух уравнений

 

 

ример 1.

Дано: ={ 15,-20,-1}, = { 0,2,1}, 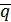_, ={ 0,1,-1}, _, = { 5,-3,2 }.

Решение:Координаты векторов 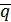_{, , ,} зададим в виде матриц размерности 31:

 

x:= , p:=s w:ascii="Cambria Math" w:fareast="Cambria Math" w:h-ansi="Cambria Math" w:cs="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>1</m:t></m:r></m:e></m:eqArr></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> , q:= , r:= .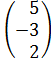

Искомое разложение вектора по векторам _{, ,} имеет вид:

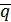= a · + b· + c ·

где a, b, c – числовые коэффициенты, являющиеся координатами вектора x в базисе { _{, ,} }. Разложение (1) приводит к системе линейных алгебраических уравнений (СЛАУ) относительно a, b, c. Найдем коэффициенты a, b, c, решая

 

систему с помощью вычислительного блока Given/Find. Матрица СЛАУ имеет вид:

A: =augment(p,q,r)=

Если матрица СЛАУ является невырожденной, то известно, что численное решение системы уравнений единственно. Поэтому для произвольных начальных значений численный метод все обеспечит сходимость к точному решению. Матрица является невырожденной, если ее определитель отличен от нуля. Вычислим определитель матрицы A, воспользовавшись стандартным оператором: |A| = - 15.

Поскольку матрица A невырожденная, возьмем начальные значения, например нулевыми. Вычислительный блок Given/Find будет иметь вид:

a:=0, b:=0, c:=0

Given

x=a · p + b · q + c · r

Для записи ответа можно воспользоваться явными символьными вычислениями. Этим термином обозначаются расчеты, в которых осуществляется простая подстановка в выражение численного значения той или иной переменной (без упрощения результата). Для организации явных вычислений предусмотрено специальное ключевое слово explicit, которое вводится с панели Symbolic (Символика).

 

Сама формула вводится в левый местозаполнитель, а переменные, числовые значения которых должны быть подставлены в нее явно и без упрощения – в правый местозаполнитель.

 

x = a × p + b × q + c × r explicit, a, b, c ® x = -6 × p +1× q + 3× r.

 

Таким образом, получили разложение вектора по векторам _{, ,}

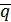следующего вида: = - 6 + + 3 .

ример 2

Дано: A(-2,4,6), B(0,2,-4), C(-6,8,-10).

Решение: Координаты точек A,B,C зададим в виде матриц размерности 3´1:

A:= , B:= , B:= ,

Чтобы найти косинус угла между векторам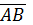и и 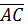, необходимо сначала найти их координаты. Координаты вектора, если известны координаты начала и конца, находятся как разность координат конца и начала вектора. Поскольку координаты точек A,B,C нам известны, можем найти координаты векторов 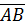и :

AB:=B - A , AC:=C - A ,

 

^

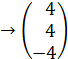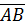Из формулы для скалярного произведения двух векторов и 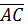следует, что:

cos( _, )=

^

Обозначим угол между векторами ()через a. Тогда получаем:

 

cos a = 1

^

Таким образом:

 

cos( _, )=-1

 

ример 3.

Дано: A₁(1,-1,2),A₂ (2,1,2),A₃(1,1,4),A₄ (6,-3,8).

Решение:

Координаты вершин зададим в виде матриц размерности 3´1:

A1:= , A2:= , A3:= , A4:= ,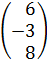

Выберем одну из вершин, например A1, и построим три вектора , , , исходящих из этой точки. Определим координаты этих векторов как разность координат точек конца и начала:

A12:=A2-A1 , A13:=A3-A1 , A14:=A4-A1 ,

Объем тетраэдра равен 1/6 объема параллелепипеда, построенного на этих векторах. А объем параллелепипеда равен модулю смешанного произведения этих векторов. Следовательно, искомый объем тетраэдра будет равен:

V:= |(A12 A13)·A14| 6

С другой стороны, объем тетраэдра равен 1/3 произведения площади основания S (грань A₁A₂A₃) на высоту h, опущенную из вершины A₄ на грань A₁A₂A₃, являющуюся треугольником. Площадь основания (треугольник D A₁A₂A₃) равна ½ площади параллелограмма, построенного на векторах , , определяемой как модуль векторного произведения этих векторов: S:= |A12´A13| ® 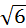. Тогда находим искомую высоту: h:=ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> ®3 .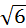

 

ример 4.

 

Дано: P ₁: x +2 y - 2 z - 7=0, P ₂: x + y - 35=0.

Решение:

 

Угол между плоскостями совпадает с углом, образованным векторами нормалей этих плоскостей. Пусть n̅₁ – вектор нормали плоскости P ₁, а n̅₂ –

̅

^

вектор нормали плоскости P ₂. Из формулы для скалярного произведения двух векторов n̅₁ и n̅₂ следует:

cos(n̅₁,n̅₂ )=

 

Координатами векторов нормалей являются коэффициенты при неизвестных в уравнениях плоскостей, записанных в общем виде. Обозначим левые части уравнений плоскостей за P ₁ и P ₂, соответственно:

P₁:=x+2y-2z-7_, P₂:=x+y-35

Коэффициенты из уравнения плоскости определим с помощью стандартного оператора · coeffs,· ® на панели Символьные:

A:= P₁ coeffs,x ,B:= P₁ coeffs,y ,

 

C:= P₁ coeffs,z ,

Искомые коэффициенты формируются в матрицы A, B, C, в которых нулевые элементы – это свободные члены, а первый элемент – соответствующий коэффициент при определяемой переменной. На случай отсутствия какой-либо переменной в уравнении плоскости необходимо переопределить первые элементы матриц A, B, C, поскольку в этом случае матрица будет содержать только один нулевой элемент, т.е. свободный член. И при обращении к первому элементу будет возникать ошибка. Поэтому необходимо на этот случай первым элементам присвоить нулевые значения с помощью оператора on error:

A₁:=0 on error A_1, B₁ :=0 on error B₁, C₁:=0 on error C₁.

Следовательно, вектор n̅₁ будет иметь координаты:

 

n̅₁:= ,

Аналогично определяем координаты вектора n̅2:

 

AA:= P₂ coeffs,x ,BB:= P₂ coeffs,y ,

CC:= P₂ coeffs,z ,

 

AA₁:= 0 on error AA₁, BB₁:= 0 on error BB₁, CC₁:= 0 on error CC₁.

 

Таким образом, вектор n̅₂ будет иметь координаты:

 

^

^

n2:= ,

Обозначим угол между векторами (n̅₁,n̅₂ ) через а. Тогда получаем:

 

s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="36"/><w:lang w:val="EN-US"/></w:rPr><m:t>a</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> :=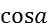

ример 5.

Дано: a ₁:2 x - 3 y - 2 z +6=0, a ₂: x - 3 y + z +3=0

Решение:

Пусть даны две плоскости a ₁ и a ₂ своими уравнениями

a 1: A 1 x + B 1 y + C 1 z + D 1 = 0	(1)
a 2: AA 1 x + BB 1 y + CC 1 z + DD 1 = 0	(2)

Известно, что систему уравнений (1),(2) (в случае непараллельных плоскостей) можно рассматривать как уравнение некоторой прямой. Чтобы составить канонические уравнения этой прямой

= =

надо определить какую-либо точку M₀(x₀; y₀; z₀), принадлежащую данной прямой, и направляющий вектор ={q₀; q₁; q₂} этой прямой. Направляющий

вектор (вектор, параллельный прямой) найдем как векторное произведение векторов нормалей данных плоскостей. Координатами векторов нормалей являются коэффициенты при неизвестных в уравнениях плоскостей, записанных в общем виде. Обозначим левые части уравнений плоскостейчерез s₁ и s₂ соответственно:

s₁:=2x-3y-2z+6, s₂:=x-3y+z+3,

Коэффициенты из уравнения плоскости определим с помощью стандартного оператора ≪ coeffs, ®·· ≫ на панели Символьные:

А:= s₁ coeffs,x® , B:= s₁ coeffs,y® ,

C:= s₁ coeffs,z® .

Искомые коэффициенты формируются в матрицы A, B, C, в которых нулевые элементы – это свободные члены, а первый элемент – соответствующий коэффициент при определяемой переменной. На случай отсутствия какой-либо переменной в уравнении плоскости необходимо переопределить первые элементы матриц A, B, C, поскольку в этом случае матрица будет содержать только один нулевой элемент, т.е. свободный член. И при обращении к первому элементу будет возникать ошибка. Поэтому необходимо на этот случай первым элементам присвоить нулевые значения с помощью оператора on error:

A₁:=0 on error A₁, B₁:=0 on error B₁, C₁:=0 on error C₁

Следовательно, вектор будет иметь координаты:

 

n̅₁:= ,

Аналогично определяем координаты вектора

AA:= s₂ coeffs,x , BB:= s₂ coeffs,y ,

CC:= s₂ coeffs,z ,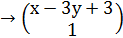

AA₁:=0 on error AA₁, BB₁:=0 on error BB₁, CC₁:=0 on error CC₁.

Таким образом, вектор будет иметь координаты:

n̅₂:= ,

Следовательно, вектор будет иметь координаты: q:=n1 n2 .

 

Найдем точку M₀, решая совместно систему уравнений с помощью блока Given\Find:

Given

s1 = 0, s2 = 0.

M:=Find(x,y,z) .

X0:=M₀ -3, y0:=M₁ 0, z0:=M₂

 

Остается подставить полученные параметры в уравнения. Введем вспомогательные параметры:

m:=q₀ -9, l:=q₁ -4, k:=q₂ -3, g:=|x0| 3, h:=|y0| 0, v:=|z0| 0.

Подстановку выполним с помощью оператора explicit:

 

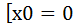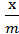a:=if , _, if , , explificit, x0, m, g

 

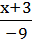
b:=if , _, if , , explificit, y0, l, h

 

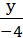
c:=if , _, if , , explificit, z0, k, v

 

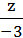
Выражения задаются условными операторами в зависимости от координат точки M₀ (больше нуля, меньше нуля или равны нулю). Таким образом, получаем канонические уравнения прямой вида:

A=b explicit,a,b ₌ , b=c explicit,b,c =

 

 

Пример 6 Дано:а) M (0,-3,-2),	x - 0.5	=	y +1.5	=	z -1.5	.
		-1

б) M (-2,0,3), a: 2 x - 2 y +10 z +1= 0

Решение:

а) Для вариантов 1–15

 

Рис. 1.

 

Для отыскания координат точки M ', симметричной точке M относительно

прямой l, надо найти координаты	точки K - середины	отрезка MM ',
перпендикулярного прямой l. Зная координаты точек M и	K,координаты
точки M ' можно найти из соотношений	.

Чтобы найти координаты точки K, используем тот факт, что точка K принадлежит прямой l, а вектор перпендикулярен направляющему вектору прямой l.

Координаты точек M, K и M1 зададим в виде матриц размерности 3´1:

M:= , M:= , M1:= ,

где M1 – искомая точка M¢. Числители в канонических уравнениях прямой обозначим за a,b,с соответственно:

a: = x - 0.5, b = y + 1.5, c = z – 1.5.

Знаменатели в канонических уравнениях – это координаты направляющего вектора 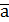. Координаты его зададим в виде матрицы размерности 3´1 и обозначим за n:

n:=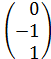

Определим координаты точки M0Î l из многочленов a,b,c (2), в которых свободные члены с противоположным знаком определяют координаты точки, принадлежащей этой прямой. Для этого воспользуемся стандартным оператором ≪ coeffs, ®·· ≫ на панели Символьные:

A:= a coeffs,x , B:= b coeffs,y , C:= c coeffs,z ,

 

 

Искомые коэффициенты формируются в матрицы A, B, C, в которых нулевые элементы – это свободные члены, а первый элемент – соответствующий коэффициент при определяемой переменной. Следовательно координаты точки M0 будут иметь вид:

M0:= ,

Составим уравнение плоскости, проходящей через точку M перпендикулярно прямой l, из условия ортогональности векторов и 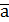. Так как векторы ортогональны, то их скалярное произведение равно нулю. Координаты вектора определим как разность координат точки K и M, а скалярное произведение векторов и 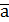обозначим через s:

MK:= , s:= MK×n

Таким образом, уравнение плоскости принимает вид:

s=0 z-y-1=0.

Найдем теперь координаты точки K, являющейся точкой пересечения данной плоскости с прямой l, решив совместно систему данных уравнений. Для этого воспользуемся вычислительным блоком Given\Find:

Given

a×n₁=b×n₀, b×n₂=c×n₁, s=0.

K:=Find(x,y,z)

Здесь n₀,n₁,n₂- координаты вектора n. Точка K является серединой отрезка MM1. А поскольку координаты середины отрезка находятся как среднее арифметическое соответствующих координат концов отрезка (см. формулы 1, 2), то координаты искомой точки M1 можно определить из системы уравнений, используя вычислительный блок Given\Find:

Given

=K

M1:=Find(x1,y1,z1))

 

 

 

б) Для вариантов 16–31.

Для отыскания координат точки M ', симметричной точке M относительно плоскости a, необходимо найти координаты точки K - середины отрезка M M ', перпендикулярного плоскости a.

Точку K найдем как точку пересечения прямой MM ' и плоскости a (см. указание к задаче 13). Заметим, что нормальный вектор плоскости a является

 

направляющим вектором прямой MM '.		Зная координаты точек M и K,
вычислим координаты точки M '	по формулам (1).
Координаты точек M, K и M1	зададим в виде матриц размерности 3´1:

M:= 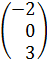, K:= , M1:= ,

где M1 – искомая точка M ¢. Составим канонические уравнения прямой MM '.

 

В качестве направляющего вектора выберем вектор нормали плоскости a. Координатами вектора нормали являются коэффициенты при неизвестных в уравнении плоскости, записанном в общем виде. Обозначим левую часть уравнения плоскости через s:

 

s:=2 x - 2 y +10 z +1.

 

Коэффициенты из уравнения плоскости определим с помощью стандартного оператора · coeffs,· ® на панели Символьные:

 

 

A:= s coeffs,x , B:= s coeffs,y ,

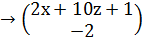C:= s coeffs,z ,

Искомые коэффициенты формируются в матрицы A, B, C, в которых нулевые элементы – это свободные члены, а первый элемент – соответствующий коэффициент при определяемой переменной. На случай отсутствия какой-либо переменной в уравнении плоскости необходимо переопределить первые элементы матриц A, B, C, поскольку в этом случае матрица будет содержать только один нулевой элемент, т.е. свободный член. И при обращении к первому элементу будет возникать ошибка. Поэтому необходимо на этот случай первым элементам присвоить нулевые значения с помощью оператора on error:

 

A₁:= 0 on error A₁, B₁:= 0 on error B₁, C₁:= 0 on error C₁.

Следовательно, вектор n̅ будет иметь координаты:

 

n:= ,

Введем обозначения:

 

X0:=M₀ -2, y0:=M₁ 0, z0:=M₂

m:=n₀ 2, l:=n₁ -2, k:=n₂ 10,

g:=|M₀| 3, h:=|M₁| 0, v:=|M₂| 3.

Подстановку выполним с помощью оператора explicit:

 

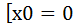a:=if , _, if , , explificit, x0, m, g

 

b:=if , _, if , , explificit, y0, l, h

 

c:=if , _, if , , explificit, z0, k, v

 

 

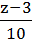
Выражения задаются условными операторами в зависимости от координат точки M ₀ (больше нуля, меньше нуля или равны нулю). Таким образом,

 

получаем канонические уравнения вида:

a=b explicit, a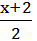,b = , b=c explicit, c,b =

 

 

Найдем теперь координаты точки K, являющейся точкой пересечения данной прямой с плоскостью a, решив совместно систему данных уравнений. Для этого воспользуемся вычислительным блоком Given\Find:

Given

s =0,l×(x - x0)=m×(y - y0),k×(y - y0)=l×(z - z0).

 

K:=Find(x,y,z)

Точка K является серединой отрезка MM1. А поскольку координаты середины отрезка находятся как среднее арифметическое соответствующих координат концов отрезка (см. формулы 1), то координаты искомой точки M1 можно определить из системы уравнений, используя вычислительный блок

 

Given\Find:

 

Given

 

=K

M1:=Find(x1,y1,z1)

 

 

 

Варианты заданий

ІІ. Написать разложение вектора по векторам _{, ,}

.1. x ={-2,4,7}, p ={0,1,2}, q ={1, 0,1}, r = {-1,2,4}.

1.2. x ={6,12,−1}, p ={1,3, 0}, q ={2,−1,1}, r ={0,−1,2}.

1.3. x ={1,−4,4}, p ={2,1,1}, q ={0,3, 2}, r ={1,−1,1}.

1.4. x ={-9,5,5}, p ={4,1,1}, q ={2, 0,−3}, r ={-1,2,1}.

1.5. x ={-5,-5,5}, p ={-2,0,1}, q ={1, 3,−1}, r ={0,4,1}.

1.6. x ={13,2,7}, p ={5,1, 0}, q ={2, −1, 3}, r ={1,0,−1}.

1.7. x ={-19,−1, 7}, p ={0,1, 1}, q ={-2,0, 1}, r ={3,1,0}.

1.8. x ={3,−3,4}, p ={1,0,2}, q ={0,1, 1}, r ={2,−1,4.}.

1.9. x ={3, 3,−1}, p ={3,1, 0}, q ={-1,2, 1}, r ={-1,0,2}.

1.10. x ={-1,7,−4}, p ={-1,2, 1}, q ={2,0, 3}, r ={1,1,−1}.

1.11. x ={6,5,−14}, p ={1,1, 4}, q ={0,−3, 2}, r ={2,1,−1}.

1.12. x ={6,−1,7}, p ={1,−2, 0}, q ={-1,1,3}, r ={1,0,4}.

1.13. x ={5,15, 0}, p ={1,0, 5}, q ={-1,3, 2}, r ={0,−1,1}.

1.14. x ={2,−1,11}, p ={1,1, 0}, q ={0, 1,−2}, r ={1,0, 3}.

1.15. x ={11,5,−3}, p ={1,0, 2}, q ={-1,0, 1}, r ={2,5,−3}

1.16. x ={8,0,5}, p ={2,0, 1}, q ={1,1, 0}, r ={4,1,2}.

1.17. x ={3,1,8}, p ={0,1, 3}, q ={1, 2,−1}, r ={2, 0,−1}.

1.18. x ={8,1,12}, p ={1, 2,−1}, q ={3,0,2}, r ={-1, 1,1}.

1.19. x ={-9,−8,−3}, p ={1,4,1}, q ={-3,2, 0}, r ={1,−1,2}.

1.20. x ={- 5,9,−13}, p ={0, 1,−2}, q ={3,−1,1}, r ={4,1,0}.

1.21. x ={-15,5,6}, p ={0,5,1}, q ={3, 2,−1}, r ={-1,1,0}.

1.22. x ={8,9,4}, p ={1,0, 1}, q ={0,−2, 1}, r ={1,3,0}.

1.23. x ={23,−14,−30}, p ={2,1,0}, q ={1,−1, 0}, r ={-3,2,5}.

1.24. x ={3,1,3}, p ={2,1, 0}, q ={1,0, 1}, r ={4,2,1}.

1.25. x ={-1,7,0}, p ={0,3, 1}, q ={1,−1, 2}, r ={2, −1,0}.

1.26. x ={11,−1,4}, p ={1,−1,2}, q ={3,2,0}, r ={-1,1,1}.

1.27. x ={-13,2,18}, p ={1,1, 4}, q ={-3,0, 2}, r ={1,2,−1}.

1.28. x ={0,−8,9}, p ={0,−2,1}, q ={3,1,−1}, r ={4,0,1}.

1.29. x ={8,−7,−13}, p ={0,1,5}, q ={3,−1, 2}, r ={-1,0,1}.

1.30. x ={2,7,5}, p ={1,0, 1}, q ={1,−2, 0}, r ={0,3,1}

ІІІ. Найти косинус угла между векторам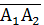и . и .

ІV. Вычислить объем тетраэдра с вершинам1и в точках A₁, A₂, A₃, A₄ и его высоту, опущенную из вершины A₄ на грань A₁A₂A₃.

2.1.

2.2.

2.3.

2.4.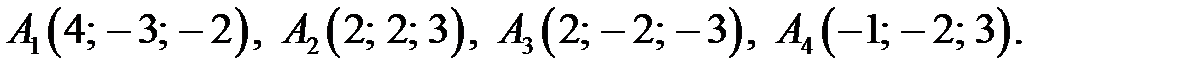

2.5.

2.6.

2.7.

2.8.

2.9.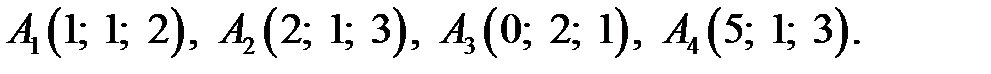

2.10.

2.11.

2.12.

2.13.