Целью работы является знакомство с основными подходами к решению проблемы удаления невидимых линий и поверхностей и изучение алгоритмов удаления невидимых лини методами «плавающего горизонта», z-буфера и Робертса.
Рекомендации по выполнению лабораторной работы:
1. Согласуйте с ведущим преподавателем номер варианта, в соответствии с которым вы будете проводить исследования. Варианты заданий представлены в таблице 5.
2. Составить программу для создания файла данных, описывающих выбранный графический примитив (набор примитивов).
3. Составить программу для построения изображения графического примитива (набора примитивов) с удалением невидимых линий, используя один из изученных алгоритмов. Исходные данные (графического примитива (набора примитивов)) считать из файла данных.
4. Сформировать отчет о ЛР, содержащий следующие пункты:
· Постановка задачи.
· Спецификации подпрограмм.
· Описание основных алгоритмов.
· Тексты программ.
· Примеры работы программы.
Таблица 5
 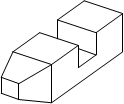 11 11
| |||
  13 13
|
ПРИЛОЖЕНИЕ 1. МАТРИЦЫ ПРОСТЫХ ДВУМЕРНЫХ ПРЕОБРАЗОВАНИЙ
| Локальное масштабирование: в a раз по координатной оси x, в d раз по координатной оси y | 
|
| Симметричное отражение относительно координатной оси x | 
|
| Симметричное отражение относительно координатной оси y | 
|
| Симметричное отражение относительно точки начала координат (поворот вокруг точки начала координат на 180°) | 
|
| Сдвиги: вдоль координатной оси x на cy, вдоль координатной оси y на bx | 
|
| Поворот на произвольный угол q относительно точки начала координат | 
|
| Отражение относительно прямой у = x | 
|
| Отражение относительно прямой у = – x | 
|
| Перемещения: вдоль координатной оси x на m, вдоль координатной оси y на n | 
|
Проецирование в однородных координатах (если  и и  , результат необходимо нормализовать путем деления всех однородных координат на h) , результат необходимо нормализовать путем деления всех однородных координат на h)
| 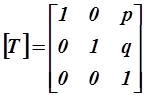
|
Общее масштабирование в  раз (если раз (если  , и , и  результат необходимо нормализовать путем деления всех однородных координат на h) результат необходимо нормализовать путем деления всех однородных координат на h)
| 
|
ПРИЛОЖЕНИЕ 2. МАТРИЦЫ ПРОСТЫХ ПРОСТРАНСТВЕННЫХ ПРЕОБРАЗОВАНИЙ
| Локальное масштабирование: в a раз по координатной оси x, в e раз по координатной оси y, в j раз по координатной оси z | 
|
| Симметричное отражение относительно координатной плоскости yz (x = 0) | 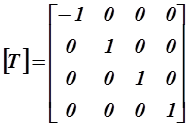
|
| Симметричное отражение относительно координатной плоскости xz (y = 0) | 
|
| Симметричное отражение относительно координатной плоскости xy (z = 0) | 
|
| Симметричное отражение относительно координатной оси x (поворот вокруг оси x на 180°) | 
|
| Симметричное отражение относительно координатной оси y (поворот вокруг оси y на 180°) | 
|
| Симметричное отражение относительно координатной оси z (поворот вокруг оси z на 180°) | 
|
| Симметричное отражение относительно точки начала координат | 
|
| Сдвиги: вдоль оси x на dy + gz, вдоль оси y на bx + iz, вдоль оси z на cx + fy | 
|
| Поворот вокруг координатной оси x на произвольный угол q | 
|
| Поворот вокруг координатной оси y на произвольный угол f | 
|
| Поворот вокруг координатной оси z на произвольный угол y | 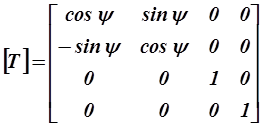
|
| Перемещения: вдоль координатной оси x на l, вдоль координатной оси y на m, вдоль координатной оси z на n | 
|
Проецирование в однородных координатах (если  и и  , результат необходимо нормализовать путем деления всех однородных координат на h) , результат необходимо нормализовать путем деления всех однородных координат на h)
| 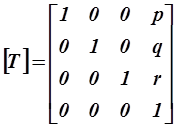
|
Общее масштабирование в  раз (если раз (если  , и , и  результат необходимо нормализовать путем деления всех однородных координат на h) результат необходимо нормализовать путем деления всех однородных координат на h)
| 
|
| Параллельное ортографическое проецирование на координатную плоскость xy (z = 0) | 
|
ПРИЛОЖЕНИЕ 3. ПРИМЕР ОТЧЕТА ПО ЛР
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«Московский государственный институт радиотехники, электроники и автоматики
(технический университет)»
МИРЭА
Факультет информационных технологий (ИТ)
Кафедра базовая автоматизированных систем организационного управления (АСОУ) №239 МИРЭА
при ФГУП НИИ «Восход»

Отчет по лабораторной работе
по дисциплине
«КОМПЬЮТЕРНАЯ ГРАФИКА»
Тема: «ИЗУЧЕНИЕ ПРИЁМОВ РАБОТЫ С ГРАФИЧЕСКИМИ РЕДАКТОРАМИ»
| Выполнил студент гр. ИТВ-2-08 | |||
| Преподаватель | Доцент | ||
| Р. Ю. Никишов | |||
| Оценка | |||
| Дата | |||
осква, 2012






