Определение. Общее уравнение поверхности второго порядка имеет вид
a 11 x 2+ a 22 y 2+ a 33 z 2+ 2 a 12 xy + 2 a 13 xz + 2 a 23 yz +
+ 2 a 1 x + 2 a 2 y + 2 a 3 z + с = 0. (18)
Выражение, записанное в первой строке, называется квадратичной частью уравнения, выражение 2 a 1 x + 2 a 2 y + 2 a 3 z называется линейной частью уравнения, а с называется свободным членом.
Квадратичная часть уравнения (18) представляет собой квадратичную форму. Обозначим её k (). Найдем новую систему координат (x ¢, y ¢, z ¢), относительно которой квадратичная форма k () имеет диагональный вид (13). Для того чтобы узнать, какой при этом вид примет линейная часть уравнения, необходимо найти формулы вида (14¢), выражающие старые координаты x, y, z через новые x ¢, y ¢, z ¢, и подставить их в линейную часть. Обратите внимание на то, что подстановку нужно делать только в линейную часть уравнения; какой вид примет квадратичная часть при такой подстановке мы можем написать сразу – это вид (13). В итоге мы получим выражение вида
l1 x ¢2 + l2 y ¢2 + l3 z ¢2 + 2 b 1 x ¢ + 2 b 2 y ¢ + 2 b 3 z ¢ + с ¢ = 0.
Теперь применим преобразование, которое называется методом выделения полных квадратов или методом Лагранжа. Предположим, что ни одна из величин l1, l2, l3, b 1, b 2, b 3 не равна нулю. Тогда последнее уравнение можно переписать следующим образом:
l1 - + l2- +
+ l3 - + с ¢ = 0.
Если и «свернуть» полные квадраты, и обозначить
d = с ¢- - -,
то получим уравнение
l12+ l22+ l32+ d = 0.
Сделаем теперь замену координат
x ²= x ¢+ b 1/l1,
y ²= y ¢+ b 2/l2,
z ²= z ¢+ b 3/l3.
Эта замена эквивалентна переносу начала координат (параллельному переносу координатных осей) в точку O ¢(- b 1/l1,- b 2/l2,- b 3/l3) Ox ¢ y ¢ z ¢. Подчеркнём, что координаты точки O ¢ указаны относительно системы Ox ¢ y ¢ z ¢. Теперь наше уравнение принимает вид
l1(x ²)2 + l2(y ²)2 + l3(z ²)2 + d = 0. (19)
Проведенные нами преобразования справедливы и в том случае, когда какая-либо из величин b 1, b 2, b 3 равна нулю; например, при b 1= 0 получим x ²= x ¢. Если l1= 0, то избавиться в уравнении от слагаемого 2 b 1 x ¢ нам не удастся. Тогда мы пока оставляем координату x ¢ без изменения. Аналогично при l2= 0 оставляем пока без изменения координату y ¢, при l3= 0 – координату z ¢.
Предположим теперь, что только одно из чисел l1, l2, l3 равно нулю. Тогда мы можем считать, что именно l3 = 0 (если это не так, мы поменяем порядок обозначения переменных). После выделения полных квадратов получим уравнение вида
l1(x ²)2 + l2(y ²)2 + 2 b 3 z ¢ + d = 0. (20)
где d = с ¢- b 12/l1 - b 22/l2. Тогда мы его преобразуем так:
l1(x ²)2 + l2(y ²)2 + 2 b 3(z ¢ + d /2 b 3) = 0
и совершаем замену координат z ²= z ¢ + d /2 b 3. Обратите внимание на то,что делать замену z ²= 2 b 3 z ¢ + d нельзя, т.к. это не будет эквивалентно переходу к новой декартовой системе координат. После замены получим уравнение вида
l1(x ²)2 + l2(y ²)2 = -2 b 3 z ². (21)
При этом мы выписываем замену координат:
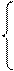x ²= x ¢+ b 1/l1,
y ²= y ¢+ b 2/l2,
z ²= z ¢ + d /2 b 3,
Эта замена означает перенос начала координат в точку O ¢(- b 1/l1,- b 2/l2,- d /2 b 3) Ox ¢ y ¢ z ¢.
Предположим, что среди чисел l1, l2, l3 только одно отлично от нуля. Тогда мы можем считать, что именно l1¹0. После выделения полных квадратов может получиться уравнение вида
l1(x ²)2 +2 b 2 y ¢ + 2 b 3 z ¢ + d = 0. (22)
Это наиболее сложный случай. Здесь необходимо сделать такую замену, чтобы вместо двух переменных y ¢ и z ¢ осталась одна переменная y ². При этом, искомая замена переменных должна осуществляться с помощью ортогональной матрицы. Этим требованиям удовлетворяет замена
y ²= (b 2/ k) y ¢ + (b 3/ k) z ¢,
z ²= - (b 2/ k) y ¢ - (b 3/ k) z ¢,
где k =. Осуществив её, получим уравнение
l1(x ²)2 +2 ky ²+ d = 0. (23)
Подобное уравнение может получиться и сразу после выделения полных квадратов. В примере 7 мы на практике разберём, какую именно следует совершить замену координат, с тем, чтобы получить сразу уравнение (23) вместо (22). Затем, мы избавляемся от свободного члена, так же как и в уравнении (20) и получаем уравнение вида
l1(x ²)2 = -2 ky ². (24)
Итак, любое уравнение кривой второго порядка может быть приведено путем перехода к новой декартовой системе координат к уравнению типа (19), (21) или (24). Если вернуться к исходным обозначениям для координат, эти уравнения примут соответственно вид
l1(x ²)2 + l2(y ²)2 + l3(z ²)2 + d = 0;
l1(x ²)2 + l2(y ²)2 = -2 b 3 z ²;
l1(x ²)2 = -2 ky ².
Далее, в зависимости от знаков величин l1, l2, l3, b 3, d, эти уравнения могут быть легко преобразованы к одному из канонических уравнений поверхностей второго порядка. Список канонических уравнений кривых и поверхностей второго порядка изложен в Приложении.
Этот же метод можно применить и для приведения к каноническому виду уравнения кривой второго порядка. Как это можно сделать показывает следующий пример.
Пример 4. Относительно декартовой системы координат Oxy на плоскости кривая определяется уравнением
3 y 2 - 4 xy + 4 x + 2 y –1 = 0. (25)
Путем перехода к новой декартовой системе координат привести уравнение кривой к каноническому виду и определить тип кривой. Изобразить кривую в системе координат Oxy.
Решение. Пусть
k () = 3 y 2 - 4 xy
есть квадратичная часть уравнения кривой. Составим матрицу A квадратичной формы k () и матрицу A - l E:
A = , A - l E =.
Характеристическое уравнение можно составить, раскрыв определитель det(A - l E) и приравняв его к нулю. Но можно воспользоваться также следующей формулой для характеристического уравнения:
l2 - (tr A)l + det A = 0.
В нашем случае получаем уравнение
l2 - 3l - 4 = 0.
Оно имеет корни l1= 4, l2 = -1. Составим матрицы A - l1 E и A - l2 E:
A - 4 E =, A + E =.
По этим матрицам составляем системы уравнений для нахождения собственных векторов и:
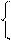
-4 x - 2 y = 0, x - 2 y = 0,
-2 x - y = 0, -2 x + 4 y = 0,
Им удовлетворяют соответственно векторы (1,-2), (2, 1). Затем находим || = , || = . Поэтому в качестве новых базисных векторов берем
,,
Матрица перехода к новому базису {, } имеет вид
С =.
Отсюда получаем формулы, связывающие старые и новые координаты:
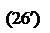
x = x ¢ + y ¢, x ¢ = x - y,
y = – x ¢ + y ¢, y ¢ = x + y,
Относительно новых координат квадратичная форма k () принимает вид
k () = l1 x ¢2 + l2 y ¢2 = 4 x ¢2 - y ¢2.
Для того, чтобы выяснить, как преобразуется линейная часть уравнения мы в линейную часть уравнения (25) подставим выражения (26). Получаем уравнение
4 x ¢2 - y ¢2 + 4 + 2 – 1 = 0.
Раскрываем скобки, приводим подобные:
4 x ¢2 - y ¢2 + 2 y ¢ – 1 = 0.
Выделим по y ¢ полный квадрат:
4 x ¢2 - (y ¢2 - 2 y ¢ + ()2) + ()2 – 1 = 0.
4 x ¢2 - (y ¢ - )2 + 5 – 1 = 0.
Теперь делаем замену переменных:
x ²= x ¢,
y ²= y ¢ - ,
которая означает перенос начала координат в точку O ¢(0, ) Ox ¢ y ¢. Получаем уравнение
4(x ²)2 - (y ²)2 = -4.
Его можно преобразовать к каноническому виду
-(x ²)2 + = 1 (27)
Данное уравнение определяет гиперболу, действительная ось которой направлена вдоль оси O ¢ y ², а полуоси равны 1 и 2.
Для того, чтобы изобразить кривую в исходной системе координат, сперва необходимо изобразить оси новой системы координат. С помощью формул (26) находим координаты точки в системе Oxy:
x = ·0 + · = 2, y = – ·0 + · =1.
Итак O ¢(2, 1) Oxy. Направление координатных осей O ¢ x ² и O ¢ y ² задаётся соответственно векторами (1,-2) и (2, 1). Мы откладываем эти векторы от точки O ¢ и затем проводим оси.
Напомним, что для изображения гиперболы сперва необходимо нарисовать фундаментальный прямоугольник (который ограничен линиями | x ²| =1, | y ²| = 2) и провести асимптоты, которые проходят через диагонали этого прямоугольника. Теперь мы вписываем обе ветви гиперболы в усеченные углы, образованные асимптотами и сторонами прямоугольника. Поскольку действительная ось гиперболы направлена вдоль O ¢ y ², мы выбираем ту пару углов, которая расположена вдоль этой оси.
| y | ||||||||||||||||||||||
| y ² | |||||||||||||||||||||||
| O ¢ | |||||||||||||||||||||||
| x | |||||||||||||||||||||||
| O | |||||||||||||||||||||||
| x ² | |||||||||||||||||||||||
Пример 5. Относительно декартовой системы координат Oxyz в пространстве поверхность определяется уравнением
3 y 2 + 4 xy - 2 xz - 4 yz + 2 x +14 y = 0.
С помощью выбора новой декартовой системы координат привести уравнение поверхности к каноническому виду.
Решение. Квадратичная часть уравнения совпадает с квадратичной формой из примера 3: k () = 3 y 2 + 4 xy - 2 xy - 4 yz. Мы уже выяснили, что с помощью выбора нового ОНБ в пространстве, мы можем привести эту квадратичную форму к виду
k () = - x ¢2 - y ¢2 + 5 z ¢2,
и при этом формулы замены координат имеют вид (17). Подставляем эту замену в линейную часть уравнения: 2 x +14 y, а квадратичную часть пишем сразу в новых координатах:
- x ¢2 - y ¢2 + 5 z ¢2 + 2 +14
Раскрываем скобки, приводим подобные:
- x ¢2 - y ¢2 + 5 z ¢2 + x ¢- 4 y ¢+ 5 z ¢ = 0.
Выделяем полные квадраты:
-(x ¢2 - x ¢ + (/2)2) + - (y ¢2 + 4 y ¢+ (2)2) +12 +
+ 5(z ¢2 + z ¢ + (/2)2) - = 0.
-(x ¢- /2)2 - (y ¢ + 2)2 +5(z ¢ + /2)2 + 5 = 0.
Делаем замену координат:
x ²= x ¢- /2,
y ²= y ¢ + 2,
z ²= z ¢ + /2.
Она означает перенос начала координат в точку O ¢(/2, –2,-/2) Ox ¢ y ¢ z ¢. После замены получаем уравнение
-(x ²)2 - (y ²)2 +5(z ²)2 = -5.
Делим его на -5 и окончательно получаем каноническое уравнение
+ - (z ²)2 = 1.
Это уравнение задаёт однополостной гиперболоид. Дополнительно можем найти координаты точки O ¢ в исходной СК. Для этого подставим найденные выше её координаты в (17). Получим O ¢(-2,1,3) Oxyz.
В следующем примере мы рассмотрим случай, когда все числа l1, l2, l3 различные. Это самый простой для решения пример.
Пример 6. Относительно декартовой системы координат Oxyz в пространстве поверхность определяется уравнением
4 x 2 + 2 y 2 + 3 z 2 + 4 xz - 4 yz + 6 x - 6 y = 0.
С помощью выбора новой декартовой системы координат привести уравнение поверхности к каноническому виду.
Решение. Составляем матрицу A квадратичной части уравнения матрицу A - l E:
A =, A - l E =.
Находим коэффициенты характеристического многочлена:
tr A = 4 + 2 + 3 = 9,
I2(A) = + + = 8 + 2 + 8 = 18,
det A = = 2· = 2·0 = 0
(мы прибавили к третьей строке вторую, а затем раскрыли определитель по второму столбцу). Составляем характеристическое уравнение в соответствии с формулой (6):
-l3 + 9l2 - 18l + 0 = 0 Û l(l2 – 9l +18) = 0.
Отсюда l1 = 0, l2 = 3, l3 = 6.
A - 0 E =,
Для данной системы наиболее удобным является следующий способ решения: из 1 и 2 второго уравнений выразить x и y через z, а потом подставить в третье уравнение для проверки.
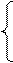x = -0,5 z,
y = z,
- z - 2 z + 3 z = 0.
Затем придаём z произвольное ненулевое значение, например, z = 2 и находим x = -1, y = 2. (–1, 2, 2).
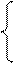A - 3 E =,
A - 6 E =.
Данные системы решаются таким же способом (проделайте это самостоятельно). Мы находим (2, 2,-1), (2,-1, 2). Теперь нормируем найденные собственные векторы, и результат оформляем следующим образом.
l1 = 0, (–1, 2, 2),,
l2 = 3, (2, 2,-1),,
l3 = 6, (2,-1, 2),.
Это является обязательным требованием к оформлению решения в контрольной работе. Составляем матрицу перехода, выписывая координаты новых базисных векторов в столбцы.
C =.
Данная матрица получилась симметрической. Поэтому она является сама к себе обратной: C · C=E. По этой же причине формулы прямой и обратной замены координат выглядят одинаково:
x ¢= (- x + 2 y + 2 z), x = (- x ¢ + 2 y ¢ + 2 z ¢),
y ¢= (2 x + 2 y - z), y = (2 x ¢ + 2 y ¢ - z ¢),
z ¢= (2 x - y + 2 z), z = (2 x ¢ - y ¢ + 2 z ¢),
Квадратичную часть уравнения в новых координатах мы выписываем сразу, а в линейную часть необходимо сделать подстановку.
0 x ¢2 + 3 y ¢2 + 6 z ¢2 + (- x ¢ + 2 y ¢ + 2 z ¢) - (2 x ¢ + 2 y ¢ - z ¢) = 0,
3 y ¢2 + 6 z ¢2 - 6 x ¢ + 6 z ¢ = 0.
Делим данное уравнение на 3 и выделяем полный квадрат по z ¢; коэффициент при x ¢ выносим за скобку.
y ¢2 + 2(z ¢2 + z ¢ + ) - - 2 x ¢ = 0,
y ¢2 + 22= 2 .
Делаем замену координат:
x ²= x ¢ + 1/4,
y ²= y ¢,
z ²= z ¢ + 1/2.
Она означает перенос начала координат в точку O ¢(-1/4, 0,-1/2) Ox ¢ y ¢ z ¢. После замены получаем уравнение
(y ²)2 + 2(z ²)2 = 2 x ² Û + (z ²)2 = x ².
Мы получили каноническое уравнение эллиптического параболоида, осью которого является O ¢ x ².
В следующем заключительном примере мы рассмотрим самый сложный случай, когда ноль является собственным числом кратности 2.
Пример 7. Относительно декартовой системы координат Oxyz поверхность определяется уравнением
x 2 + y 2 + z 2 + 2 xy + 4 xz + 4 yz + 8 x + 4 y - 5 = 0.
С помощью перехода к новой декартовой системе координат привести уравнение поверхности к каноническому виду и определить тип поверхности.
Решение. Пусть k () = x 2 + y 2 + z 2 + 2 xy + 4 xz + 4 yz – квадратичная часть уравнения поверхности. Составим матрицу квадратичной формы k () и матрицу A - l E:
A =, A - l E =.
Находим коэффициенты характеристического многочлена:
tr A = 1 + 1 + 4 = 6,
а поскольку, очевидно, rank A =1 (т.к. все строки в A пропорциональны), то I2(A) = 0 и det A = 0. Составляем характеристическое уравнение в соответствии с формулой (6):
-l3 + 6l2 = 0 Û l2(l - 6) = 0.
Значит, l1 = 0, l2 = 0, l3 = 6. Для собственного числа l3 = 6 обычным образом находим собственный вектор (1, 1, 2).
При l1 = l2 = 0 система уравнений для нахождения собственных векторов имеет ранг 1:
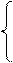
Поэтому, так же, как и в примере 2, оставляем первое уравнение
x + y + 2 z = 0, (28)
а остальные уравнения отбрасываем. Этому уравнению удовлетворяет, например, вектор (1,-1, 0). Если мы воспользуемся таким вектором, то получим после замены уравнение вида (22). После этого потребуется решать проблему дополнительной замены координат. Наша цель: совершить замену координат так, чтобы после замены в уравнении не осталось координаты x ¢ или координаты y ¢ (поскольку в квадрате у нас будет только одна координата z ¢). Если координаты вектора (x, y, z) будут удовлетворять дополнительному условию a 1 x + a 2 y + a 3 z = 0, то после замены в уравнении не останется x ¢, а если этому условию будут удовлетворять координаты, то после замены не останется y ¢. В нашем случае данное условие выглядит так: 4 x + 2 y = 0. Поэтому координаты вектора будем искать из системы
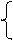Û
Отсюда (2,- 4, 1). Вектор (x, y, z) должен удовлетворять условию (28), а также должен быть ортогонален, т.е. (x, y, z)· (2,- 4, 1) = 0. Итак, координаты (x, y, z) мы ищем из системы
Û Û
Отсюда (3, 1,-2). Теперь нормируем найденные собственные векторы, и результат оформляем следующим образом.
l1 = 0, (2,- 4, 1),,
l2 = 0, (3, 1,-2),,
l3 = 6, (1, 1, 2),.
Выражение старых координат через новые мы можем выписать сразу, не составляя матрицы перехода.
x = x ¢ + y ¢ + z ¢,
y = - x ¢ + y ¢ + z ¢,
z = x ¢ - y ¢ + z ¢.
Квадратичную часть уравнения в новых координатах мы выписываем сразу, а в линейную часть необходимо сделать подстановку.
6 z ¢2 + 8 + 4 - 5 = 0,
6 z ¢2 + 
y ¢ + z ¢ - 5 = 0 Û 3 z ¢2 + y ¢ + z ¢ - 2,5 = 0,
Выделим по z ¢ полный квадрат:
3 - + 
y ¢ - 2,5 = 0,
32- + y ¢ - 2,5 = 0,
32+ = 0,
Делаем замену координат:
x ²= x ¢,
y ²= y ¢ -,
z ²= z ¢ +,
которая означает перенос начала координат в точку O ¢(0, ,-) Ox ¢ y ¢ z ¢. В результате получаем уравнение
3(z ²)2 = - y ².
Его можно преобразовать к каноническому виду (z ²)2 = -2 py ², где p =. Это уравнение определяет параболический цилиндр, ось которого направлена вдоль отрицательного направления координатной оси O ¢ y ², а образующие параллельны оси O ¢ x ².
Приложение 1
Список кривых второго порядка
| Название кривой | Каноническое уравнение кривой |
| 1. Эллипс | + = 1 |
| 2. Мнимый эллипс (Æ) | + = –1 |
| 3. Гипербола | – = 1 |
| 4. Пара пересекающихся прямых | a 2 x 2 – b 2 y 2 = 0 |
| 5. Пара мнимых прямых пересекающихся в действительной точке | a 2 x 2 + b 2 y 2 = 0 |
| 6. Парабола | y 2 = 2 pх, |
| 7. Пара параллельных прямых | x 2 = a 2 |
| 8. Пара мнимых параллельных прямых | x 2 = – a 2 |
| 9. Пара совпадающих прямых | x 2 = 0 |
Приложение 2
Список поверхностей второго порядка
| Название поверхности | Eё каноническое уравнение |
| 1. Эллипсоид | + + =1, |
| 2. Мнимый эллипсоид (Ø) | + + = –1, |
| 3. Мнимый конус (точка) | + + = 0, |
| 4. Двуполостной гиперболоид | + – = –1, |
| 5. Однополосной гиперболоид | + – = 1, |
| 6. Конус | + – = 0, |
| 7. Эллиптический параболоид | + = 2 z, |
| 8. Гиперболический параболоид | – = 2 z, |
| 9. Эллиптический цилиндр | + =1, |
| 10. Мнимый эллиптический цилиндр | + = –1, |
| 11. Пара мнимых плоскостей, пересекающихся по действительной прямой | + = 0, |
| 12. Гиперболический цилиндр | – = 1, |
| 13. Пара пересекающихся плоскостей | – = 0, |
| 14. Параболический цилиндр | x 2 = 2 py |
| 15. Пара параллельных плоскостей | x 2 = a 2 |
| 16. Пара совпадающих плоскостей | x 2 = 0 |
| 17. Пара мнимых параллельных плоскостей | x 2 = – a 2 |
