бщие теоретические сведения.

Рассмотрим зубчатые механизмы (передачи), составленные из колёс с прямыми зубьями.

Нулевая зубчатая передача составляется из нулевых колёс (x₁ = x₂ = 0) или при условии x₁ = -x₂ (равносмещённая передача). Делительные окружности колёс нулевой зубчатой передачи касаются в полюсе Р и в процессе зацепления перека­тываются друг по другу без скольжения, т.е одновременно являются и начальными окружностями колёс (рис. 8, а) r_w = r = 0,5mz.

Межосевое расстояние равно сумме радиусов делительных окружностей a_w = r₁ + r₂ = 0,5mz₁(z₁ + z₂) и называется де­лительным межосевым расстоянием. Угол зацепления нулевой передачи a_w = a = 20°.

Положительная зубчатая передача может быть составлена из двух положительных зубчатых колес x > 0 или из одно­го положительного и другого нулевого и, наконец, из одного положительного и другого отрицательного. В последнем случае коэффициент смещения положительного колеса по абсолютной величине должен быть больше, чем отрицательного. Дели­тельные окружности колёс положительной зубчатой передачи не касаются друг друга, начальные окружности больше дели­тельных, т.е r_w > r, межосевое расстояние равно сумме радиусов начальных окружностей (рис. 8, б).

(49)

При этом межосевое расстояние a_w > a, а угол зацепления положительной зубчатой передачи a_w > a.

 

Рисунок 8 – Зубчатое зацепление

Отрицательная зубчатая передача составляется из двух отрицательных зубчатых колёс, из одного отрицательного и другого нулевого или из одного отрицательного и другого положительного. В последнем случае коэффициент смещения от­рицательного зубчатого колеса должен быть по абсолютной величине больше, чем положительного. Делительные окружно­сти зубчатой передачи пересекаются (рис. 6, в). Радиусы делительных окружностей больше радиусов начальных окружно­стей (r > r_w); межосевое расстояние определяется по той же формуле, что и для положительной передачи. Для отрицатель­ной передачи a_w < a и a_w < a.

При проектировании следует учитывать особенности каждого вида передач. Наилучшими качествами обладают поло­жительные зубчатые передачи вследствие того, что у них больше радиусы кривизны боковых поверхностей зубьев. Кроме того, при тех же значениях передаточного числа и модуля они имеют меньшие габариты и вес.

Нулевые передачи имеют худшие эксплуатационные качества, чем положительные. Однако в настоящее время они наи­более часто применяются в машинах, так как очень просто рассчитываются и удовлетворяют принципу сменности колёс. Самые плохие эксплуатационные качества имеет отрицательная передача.

Согласно ГОСТ 16532-70 зубчатая передача, у которой оба зубчатых колеса нулевые, называется зубчатой передачей без смещения, а зубчатая передача, у которой хотя бы одно колесо изготовлено со смещением, называется зубчатой переда­чей со смещением.

Два любых зубчатых колеса, изготовленные одной и той же инструментальной рейкой, могут образовать правильное плотное зубчатое зацепление, т.е. зацепление без боковых зазоров между зубьями. В беззазорном зацеплении как рабочие, так и нерабочие стороны зубьев находятся в контакте одновременно. При этом толщина зуба (S_w) по дуге начальной окруж­ности одного колеса должна быть равна ширине впадины (e_w) по дуге начальной окружности второго и наоборот:

S_w1 = e_w2 (50)

S_w2 = e_w1

Основными величинами, характеризующими зацепление зубчатых колес являются: a_w - угол зацепления; x_S = x₁ + x₂ - суммарный коэффициент смещения; у- коэффициент воспринимаемого смещения; a - делительное межосевое расстояние.

В общем случае, в зависимости от значений указанных величин зубчатые зацепления классифицируются следующим образом:

1) номинальное зацепление (a_w = a, x₁ = x₂ = 0, a_w = a, y = 0);

2) равносмещённое зацепление (a_w = a, x₁ = -x₂, a_w = a, y = 0);

3) неравносмещённое зацепление (a_w ≠ a, x_S ≠ 0, a_w ≠ a, y > 0).

Формулы для указанных зацеплений даны в табл. 1.

Нарезая зубчатые колёса с различным смещением, можно получить зубчатую передачу с необходимыми свойствами. Не всегда удается спроектировать зубчатый механизм, отвечающий требованиям конструкции при стандартном модуле (m).

Для оценки спроектированной зубчатой передачи приняты следующие качественные показатели: коэффициент удель­ного давления q, характеризующий влияние геометрических параметров на контактную прочность и выкрашивание зубьев; коэффициент перекрытия e, показывающий характер нагружения зубьев; коэффициент относительного скольжения X, опре­деляющий влияние геометрических параметров на износ зубьев и заедание; коэффициент формы зуба у, характеризующий изгибную прочность зубьев.

Все эти качественные показатели являются функцией выбираемых коэффициентов смещения. Увеличивая коэффициен­ты смещения каждого колеса и их суммы, можно повысить контактную прочность передачи, так как при этом уменьшаются коэффициенты удельного давления; повысить износостойкость колёс и уменьшить их склонность к заеданию, так как уменьшаются коэффициенты скольжения; увеличить изгибную прочность зубьев, так как увеличивается коэффициент фор­мы зуба. Но, с другой стороны, с увеличением коэффициентов смещения уменьшается коэффициент перекрытия. Выбирая расчётные коэффициенты смещения, следует учитывать конкретные условия работы проектируемой зубчатой передачи: её быстроходность, изменяемость или цикличность нагрузки, условия смазки и т.д.

Однако расчётные коэффициенты смещения любой зубчатой передачи прежде всего должны обеспечить отсутствие за­клинивания, подреза и заострения зубьев, а также гарантировать минимально допустимую величину коэффициента перекры­тия.

В общем случае при изготовлении колёс (z,) и (z₂) со сдвигом режущего инструмента x, ≠ 0; x₂ ≠0; x, + x₂ ≠0 мон­тажный угол зацепления не равен профильному углу исходного контура (a_w≠ a).

Монтажный угол зацепления определяется из зависимости (51):

где y— коэффициент воспринимаемого смещения: .

Величина суммарного коэффициента коррекции зацепления связана с величиной угла зацепления

(52)

где inva = tga - a - эвольвентная функция.

Полученная величина x_S может быть распределена между колёсами в общем случае произвольно. Однако с целью по­вышения сопротивляемости рабочих поверхностей заеданию и контактному разрушение рекомендуется значения этих коэф­фициентов выбирать по зависимостям:

(53)

Если габариты зубчатой передачи не ограничиваются величиной a_m, то коэффициенты коррекции назначаются из со­ображений повышения эксплуатационных показателей зубчатых колёс. Одним из таких показателей является отсутствие подрезания и заострения зубьев.

Для устранения подрезания зубьев при изготовлении колёс режущий инструмент сдвигают на величину + xm, где z— число зубьев исправляемого колеса.

(54)

При большом положительном сдвиге режущего инструмента возможно пересечение эвольвент, образующих рабочие профили. Это явление называется заострением зуба (рис. 9). Для стандартного исходного контура предельное значение ко­эффициента смещения, превышение которого при изготовлении приводит к заострению зубьев, определяется из зависимо­сти: x.₃ = 0,5z.

Рисунок 9 – Заострение зуба

Для любого исходного контура может быть применена зависимость:

 

где

(55)

Таким образом, назначаемые коэффициенты смещения должны выбираться из диапазона значений х_п < х < х_з.

Существуют несколько систем коррекции, обеспечивающих определенные свойства зацепления, а именно: отсутствие подрезания зубьев, обеспечение заданного межцентрового расстояния, повышенной контактной прочности зубьев и повы­шенной износостойкости. При инженерных расчётах можно воспользоваться рекомендациями табл. 1 и 2.

Таблица 1 - Свободный выбор межосевого расстояния

 

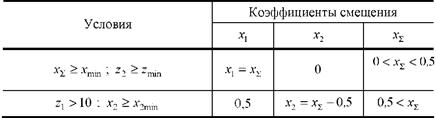
Таблица 2 – Вписывание в заданное межосевое расстаяние

 

Порядок построения зубчатого зацепления.

По вычисленным параметрам проектируемая зубчатая передача строится следующим образом:

1. Провести осевую линию и на ней выбрать центры колес О₁ и O₂, полюс зацепления Р (точка касания начальных ок­ружностей), т.е.

где a_w - межосевое расстояние; r_w1; r_w2 - соответственно радиус начальной окружности шестерни и колеса (рис. 10).

2. Провести делительные и основные окружности радиусами г12 и гЬ12.

3. Построить теоретическую линию зацепления как касательную к основным окружностям, проходящую через полюс зацепления Р-АВ.

4. Построить эвольвенты зубьев 1-го и 2-го колёс.

5. Построение эвольвенты 1 -го колеса:

- на основной окружности от точки А провести дугу uAP', равную длине отрезка AP;

- разделить прямую AP и дугу uAP' на четыре равные части. На прямой получаются точки Р, 1, 2, 3, 4, а на дуге - точки Р, 1, 2, 3. При этом 1P = u1'P'; 12 = u1'2' и т.д.;

- такие же отрезки деления откладываются по другую сторону от точки А. На прямой отмечаются точки 5, 6, 7, 8..., на дуге - точки 5, 6, 7, 8...;

- к радиусам O₁ - 1, O₁ - 2' и т.д. в сторону полюса восстановить перпендикуляры, на которых отложить отрезки 1'Г = 1P, 2'2'' = 2P и т.д.

- точки Р, 1", 2, 3, 4, 5, 6, 7, 8' соединяем лекальной кривой. Построенную эвольвенту ограничиваем по высоте зуба в точке пересечения эвольвенты с окружностью вершин зубьев (r_a1);

- выделить практическую часть линии зацепления аЬ (пересечение окружностей вершин с теоретической линией зацеп­ления).

Аналогично строится эвольвента зубьев 2-го колеса.

6. Построить ножку зуба. Профиль ножки зуба колеса состоит из эвольвентной части и переходной кривой (галтели), которая соединяет эвольвентную часть с окружностью впадин. На практике пользуются упрощённым методом построения, для чего:

- проводим окружности впадин для 1-го и 2-го колёс соответствующими радиусами r f 1 и r f 2;

- от точек пересечения эвольвенты с основными окружностями в направлении O и O проводим радиальные прямые;

- от точек пересечения эвольвенты с основными окружностями в направлении O и O проводим радиальные прямые;

- строим сопряжение этих радиальных прямых с окружностями впадин радиусом r = 0,2m.

7. Построить полный зуб, для чего:

- по дуге делительной окружности (от точки пересечения эвольвенты с делительной окружностью) отложить толщину зуба, определяемую по формуле: S12 = —m ± 2x12m tga; и толщину впадины, определяемую по формуле: e12 = pm - S12;

- провести оси симметрии зубьев и построить полные зубья (с левым и правым профилями) первого и второго зубчатых колёс, используя шаблон.

 

 

Рисунок 10 – Построение зацепления

 

формление отчета

Отчет должен содержать:

1. Наименование работы.

2. Цель работы.

3. Основные формулы.

4. Решение.

5. Вывод по решенной задаче.

адания

По исходным данным в прямозубой передаче без смещения по принятому делительному модулю m и числу зубьев шестерни z₁ и колеса z ₂определить основные размеры и построить зубчатое зацепление. (см. Табл. 4)

Таблица 4 – Исходные данные

Вариант	Модуль,мм	Количество зубьев шестерни, z1	Количество зубьев колеса, z2
	2,5
	2,75
	3,5
	4,5
	5,5

 

4. Контрольные вопросы

1. Из каких колес состоит нулевая зубчатая передача?

2. Чему равно межосевое расстояние?

3. Из каких колес состоит положительная зубчатая передача?

4. Чему равен угол зацепления нулевой передачи?

5. Из каких колес состоит отрицательная зубчатая передача?

6. Какие зубчатые передачи имеют лучшие эксплуатационные качества и почему?

7. Какие основные величины характеризуют зацепление зубчатых колес?

8. Что такое коэффициент смещения?

Приложения

Приложение 1

Значения масштабных коэффициентов при изгибе и кручении для ста-

лей приведены на рисунке. Как видно из графиков, масштабный фактор оказывает более сильное влияние на детали из высокопрочных сталей и особенно при наличии концентрации напряжений.

Рис П2. Значения коэффициентов влияния абсолютных размеров при изгибе: 1 – углеродистая сталь, гладкий полированный вал; 2 – углеродистая сталь, гладкий шлифованный вал; 3 – легированная сталь, гладкий полированный вал; 4 – легированная сталь, гладкий шлифованный вал; углеродистая сталь, деталь с концентрацией напряжений; 5 – легированная сталь, деталь с умеренной концентрацией напряжений (K σ < 2); 6 – конструкционная сталь резкой концентрацией напряжений.

Приложение2

 

Литература

Основная

1. Справочное пособие для инженеров и изобретателей. Артоболевский И.И.Механизмы в современной технике. М: Наука. Справочное пособие в 7 томах.2010г.

2. Дунаев П.Ф. Конструирование узлов и деталей машин: учеб.пособие для студ. высш. учеб. заведений /Дунаев П.Ф, Леликов О.П. – 9-е изд., перераб. доп. – М.: Издательский центр «Академия», 2009. – 496 с.

Дополнительная

3. Куклин Н.Г., Куклина Г.С. Детали машин: учеб.для машиностроит. спец.техникумов /Куклин Н.Г., Куклина Г.С. - 4-е изд., перераб. И доп. – М.: Высш. Шк., 1987. – 383 с.: ил.

4. Марков Н.Н., Ганевский Г.М. Конструкция, расчет и эксплуатация измерительных инструментов и приборов /Марков Н.Н., Ганевский Г.М. – М.: Машиностроение, 1981. – 367 с., ил.

5. Романов А.В. «Допуски изделий и средства измерений»: Справочник для учащихся ПТУ, техникумов и молодых рабочих. – СПб.: Политехника, 2003. – 291с.; ил.

6. Фролов К.В., Попов С.А. и др. Теория механизмов и механика машин: Учеб. Для вузов /Фролов К.В., Попов С.В. и др.; под ред. Фролова К.В. – 5-е изд., стереотип. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2004. – 604 с.: ил.

7. Иванов М.Л. Детали машин: Учеб. для студентов втузов/Под ред. В.А. Финогенова. — 6-е изд., перераб. — М.: Высш. шк., 2000. — 383 с: ил.

8. Левитский Н. И. Теория механизмов и машин [Текст]: учеб. пособие / Левитский Н. И. - 2-е изд., перераб. и доп. - М.: Наука, 1990. - 592 с.: ил.

9. Якушев А.И. «Взаимозаменяемость, стандартизация и технические измерения»: учебн. Для ВУЗов – 6-е изд., перераб и дополн. – М.: Машиностроение, 1986. – 352с, ил.

10. Теория механизмов и машин. Методические указания к выполнению курсового проекта / Новосиб. гос. аграр. ун-т; Сост. Ю.И. Евдокимов. – Новосибирск, 2008. – 60 с.

Интернет- источники, базы данных, информационно- справочные и поисковые системы

1. Колеса зубчатые. Виды повреждений. Классификация и описание. Межгосударственный гост стандарт.

Режим доступа:

http://www.imash.ru/normatdok/etc_gosts/3355-kolesa-zubchatye-vidy-povrezhdenijj..html

2. Лекции по Теории механизмов и машин

Режим доступа: http://www.studfiles.ru/dir/cat34/subj1330/file17438/view164166.html

3. Основы проектирования передаточных механизмов: Учебное пособие для студентов высших учебных заведений Кушнаренко В.М., Ковалевский В.П., Чирков Ю.А.

Режим доступа: http://window.edu.ru/window_catalog/pdf2txt?p_id=2512&p_page=12

 

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ ПО ДИСЦИПЛИНЕ
«ОСНОВЫ РАСЧЕТА И ПРОЕКТИРОВАНИЯ ИЗМЕРИТЕЛЬНЫХ
МЕХАНИЗМОВ»

 

Подписано в печать Формат 60×84/16. Бумага для множ. аппаратов.

Печать плоская. Усл. печ. л.. Уч.-изд. л.. Тираж экз. Заказ №.

ФГАОУ ВПО «Российский государственный профессионально-педагогический университет». Екатеринбург, ул. Машиностроителей, 11.

а

 

Ризограф ФГАОУ ВПО РГППУ. Екатеринбург, ул. Машиностроителей, 11.