1. Разработайте математическую модель движения железнодорожного состава. В первом приближении вагоны можно считать абсолютно жесткими телами, связи между ними – линейными или нелинейно упругими.
2. Выполнить содержательную, концептуальную и математическую постановки для математической модели, описывающей взлет космического аппарата с Луны.
3. Выполнить содержательную, концептуальную и математическую постановки для математической модели, описывающей посадку спутника в атмосфере Земли.
4. Выполнить содержательную, концептуальную и математическую постановки для математической модели, описывающей движение шарика в сферической ямке. Выбрать и реализовать метод решения полученной математической задачи. Исследовать траектории шарика в зависимости от начальных условий.
5. Выполнить содержательную, концептуальную и математическую постановки для математической модели, описывающей движение срубленного дерева.
6. Выполнить содержательную, концептуальную и математическую постановки для математической модели, описывающей движение заряженной частицы в магнитном поле.
7. Космический аппарат совершает движение по орбите вокруг Земли и может быть виден некоторым наблюдателем, находящимся на ее поверхности в точке с заданными координатами. Выполнить содержательную, концептуальную и математическую постановки для математической модели, описывающей движение космического аппарата по небосводу Земли с точки зрения наблюдателя.
8. Выполнить содержательную, концептуальную и математическую постановки для математической модели, описывающей движение лыжника, выполняющего прыжок с трамплина.
9. Выполнить содержательную, концептуальную и математическую постановки для математической модели, описывающей процесс нагревания и закипания чайника.
10. Постройте экономическую модель спроса и предложения в предположении их линейной зависимости от цены. Проведите анализ изменения цен в зависимости от начальной цены при следующих исходных данных a=3, b=2, c=6, g=8. Определите, в каких пределах может изменяться начальная цена.
11. Постройте экономическую модель спроса и предложения в предположении, что справедливы зависимости
sn+1 = а pnm – b,dn+1 = g exp(-c pn+1),
где a, b, c, g > 0; 0< m <1. Проведите анализ изменения цен в зависимости от начальной цены при следующих исходных данных a=3, b=2, c=1, g=8, m=0,5. Определите, как влияет значение начальной цены на сходимость решения.
12. Пусть в некоторой местности обитают две популяция животных, причем животные одной популяции относятся к хищникам, а другой – к травоядным, служащие пищей для хищников. Для описания подобных систем хищник-жертва французский математик Вольтерра в 30-е годы ХХ века предложил следующую математическую модель
,
где х – численность популяции жертв, y – численность популяции хищников. Предложите систему гипотез на основании которых Вольтера записал свою математическую модель. Какая модель (Мальтуса или Ферхюльста) была использована для описания изменения численности жертв? Проведите качественный анализ данной системы уравнений.
13. Используя модель Ферхюльста для описания поведения жертв, предложите свой вариант математической модели хищник-жертва. Проведите качественный анализ полученной системы уравнений. Выполните анализ численной схемы для данной системы.
14. При изучении развития эпидемии некоторого заболевания обычно выделяют три группы людей: x – группа людей, восприимчивая к данному заболеванию, но еще не заразившаяся им; y – группа уже больных или инфицированных людей, которые могут выступать разносчиками болезни; z – группа людей, невосприимчивых к данной болезни, или получившие иммунитет после перенесенного заболевания. Один из вариантов математической модели развития эпидемии может быть записан в следующем виде
.
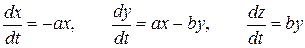Предложите систему гипотез для обоснования данной модели. Поясните смысл коэффициентов a и b. Проведите качественный анализ полученной системы уравнений. Выполните анализ численной схемы для данной системы. Предложите другие варианты моделей эпидемии с учетом
а) изменения общей численности населения, связанные с рождениями и естественными смертями;
б) смертности от данного заболевания;
в) непостоянства доли заболевших людей.
15. Одна группа медиков ищет спонсоров для исследований стоимостью в 1 млн. долл. и рассчитывает за один год получить вакцину, которая позволит уменьшить коэффициент а (см. предыдущий пример) на 25%. Другая группа медиков предлагает за один год тоже за 1 млн. долл. найти лекарство, которое увеличит на 25% коэффициент b. Если у спонсора есть только 1 млн. долл., то какую группу медиков он должен поддержать?
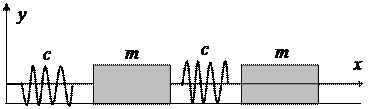
16. Сформулируйте концептуальную и математическую постановку для модели, описывающей свободные колебания системы, включающей два тела массы m, соединенных пружинами жесткостью с. Постройте траектории движения тел в фазовом пространстве.
17. Лодку массы m оттолкнули от берега пруда и, разогнав, отпустили при некоторой начальной скорости v0. Необходимо исследовать движение лодки в предположении, что сила сопротивления движению прямо пропорциональна скорости. Коэффициент сопротивления движению m. Получить аналитическое и численное решение задачи.
18. 
Постройте одномерную структурную модель упрочняющегося упругопластического тела, для которого задана диаграмма s-e приведенного вида (sS,a,b считать известными). Постройте определяющие соотношения, соответствующие вашей структурной модели.
19. На участке имеется N однотипных станков. Производительность одного станка такова, что в среднем в течение смены на нем можно обработать l деталей. Детали поступают на обработку партиями по М штук. Партии поступают неравномерно и их поток близок к пуассоновскому. Интенсивность поступления составляет l партий в смену. Требуется построить граф состояний данной СМО и записать систему уравнений Колмогорова для финальных вероятностей.
20. Мастерская по ремонту имеет складское помещение на М мест. В мастерской работают N мастеров, обеспечивающих среднее время ремонта T. Интенсивность поступления заявок l. Если все мастера заняты и склад заполнен, то заявка отклоняется. Требуется построить граф состояний данной СМО и записать систему уравнений Колмогорова для финальных вероятностей.
21. Определить требуемое число коек в стационаре больницы, если среднее время выздоровления одного больного составляет 21 день. Новые больные не принимаются, если все койки в стационаре заняты. Поток поступления больных близок к пуассоновскому с интенсивностью 3 человека в день. Вероятность отказа не должна быть выше 95%.
22. Определить среднюю длину очереди в кассу магазина, если среднее время обслуживания одного покупателя составляет 0,3 минуты. Поток покупателей близок к пуассоновскому с интенсивностью 3 покупателя в минуту. Сколько необходимо установить касс, если интенсивность потока возрастет в 5 раз? Средняя длина очереди при этом не должна превышать 10 человек.
23. Разработать имитатор одноканальной СМО с ограниченным временем ожидания в очереди. Предполагается, что поток заявок, поступающий в систему, является простейшим. Поступившая в систему заявка может сразу поступить на обслуживание, если канал свободен, либо встать в очередь. Если время пребывания заявки в очереди превысило некоторое предельное для нее значение, то она покидает систему не обслуженной. Интервал времени Dt между поступлением 2-х соседних заявок, максимальное время пребывания заявки в очереди Dh и время ее выполнения Dw описываются случайными величинами, подчиненными показательному распределению с заданными средними значениями. Имитатор должен выполнять оценку следующих параметров эффективности СМО:
· среднего времени пребывания заявки в очереди;
· вероятности выполнения заявок;
· коэффициента загрузки системы.
24. Аналогично заданию 23 разработать имитатор n-канальной СМО с ограниченным временем пребывания в очереди.
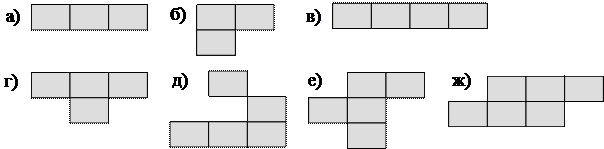
25. 
Разработать программу, реализующую клеточный автомат «Жизнь». Вывод о состоянии клеточного пространства осуществить на экран в графическом режиме. Исследуйте эволюцию КА для следующих начальных состояний, задающих расположение «живых» клеток:
 |
26. Разработайте клеточный автомат «Лишайники», поведение которого подчинено следующим правилам:
· Клетка может находиться в активном или пассивном состоянии.
· Клетка становится активной, если в 8 соседних клетках находится N1, N2 или N3 активных клеток.
· Если число активных клеток в окрестности не равно N1, N2 или N3, то клетка становится пассивной.
27. Разработайте клеточный автомат «Дюны», поведение которого подчинено следующим правилам:
· Клетка может находиться в активном и пассивном («спрятанном») состоянии.
· Если клетка была активна и из 8 соседних клеток более N активны, то клетка "прячется". Время нахождения в «спрятанном» состоянии равно W тактов.
· Если время "прятания" закончилось и в окрестности не более М активных клеток, то клетка вновь становится активной.
28. Разработайте клеточный автомат «Термит», поведение которого подчинено следующим правилам:
· Клетка может находиться в пассивном или активном состоянии. В начальный момент все ячейки пассивны, «Термит» расположен в центральной клетке и направлен кверху.
· «Термит» переходит на соседнюю клетку и если она активная, то делает ее пассивной и поворачивает налево на 90 градусов. Если клетка была пассивна, «Термит» делает ее активной и поворачивает направо на 90 градусов.
