Последовательность выполнения задания следующая.
На эпюре (рис. 11) по заданным координатам строим точку O (
) – центр шара и фронтальные проекции 
точек АВD, образующие треугольник следов граней отверстия. Далее тонкими линиями из центра О (О1,О2) проводим фронтальный и горизонтальный очерки сферы (окружности R=50 мм).
Рис. 11 Пример выполнения задания 6
Поскольку грани отверстия перпендикулярны плоскости П2, то на фронтальной проекции решение является очевидным и определяется треугольником следов А2В2D2.
Прежде, чем начать построения на горизонтальной плоскости проекций, необходимо вспомнить, что любая плоскость пересекает сферу по окружности, ориентация которой в пространстве определена положением самой секущей плоскости. Здесь следует различать три основных случая:
а) секущая плоскость перпендикулярна горизонтальной плоскости проекций П1 (является горизонтально проецирующей). В этом случае окружность на горизонтальной плоскости проекций П1 вырождается в отрезок;
б) секущая плоскость параллельна горизонтальной плоскости проекций П1. В этом случае окружность проецируется на неё натуральной формой и величиной;
в) секущая плоскость ориентирована в пространстве произвольным образом. В этом случае окружность проецируется на горизонтальную плоскость проекций П1 в виде эллипса.
Анализ условий задачи позволяет установить, что каждая из граней отверстия может быть рассмотрена как некоторая плоскость, пересекающая сферу по одному из трех указанных вариантов.
Действительно, правая грань отверстия, заданная следом B2D2, соответствует первому случаю, т.е. отрезку 
(см. рис.11) на плоскости П1.
Нижняя грань отверстия, заданная следом 
, соответствует второму случаю, т.е. окружность - параллель 
на плоскость П1 проецируется в натуральную величину. Ее центр расположен в точке О1, а радиус равен 
.
Левая грань отверстия, заданная следом А2В2, соответствует третьему случаю, т.е. окружность на плоскость П1 проецируется в виде эллипса, фронтальные проекции всех точек которого известны и принадлежат отрезку А2В2.
Эту задачу можно решить без применения способа вспомогательных поверхностей. Задать точку на поверхности вращения или построить вторую проекцию, если одна известна, можно при помощи параллели, которая проходит через эту точку. Поэтому горизонтальные проекции точек, принадлежащих линии пересечения, строим при помощи параллелей поверхности шара.
Сначала строим опорные точки линии пересечения. Прежде всего, это точки A,B и D пересечения ребер отверстия с поверхностью шара.
Через точки 
и 
проводим фронтальную проекцию параллели -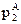 
и определяем её радиус - . На плоскости 
строим горизонтальную проекцию параллели - 
, т.е. из точки 
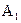проводим окружность радиусом . Горизонтальные проекции 
и 
точек A и D определяем в пересечении и линий связи, проведенных через точки и соответственно.
Точку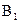 
строим по аналогичной схеме при помощи параллели 
.
Далее строим горизонтальные очерковые точки 
, принадлежащие линии АВ. Эти точки являются точками смены видимости линии на плоскости проекций . Они принадлежат экватору, а их горизонтальные проекции 
принадлежат горизонтальному очерку шара.
Строим точки 
, которые являются самой дальней и самой ближней точками относительно фронтальной плоскости проекций. Для этого из точки 
опускаем перпендикуляр на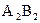 
и определяем точку 
. Через неё проводим фронтальную проекцию параллели 
и далее по схеме.
Промежуточные точки 
и 
на грани АВ выбираем произвольно и строим по аналогичной схеме. Количество промежуточных точек определяется требуемой точностью построения линии. Полученные точки соединяем плавной кривой тонкой линией.
Обводим чертеж с учетом видимости линий.
Фронтальные очерки шара и отверстия изображаем линиями видимого контура.
На горизонтальной плоскости проекций видимым участком линии 
является участок 
, расположенный выше плоскости видимости D (рис. 16) на верхней обращенной к наблюдателю половине поверхности шара. Точка 
так же, как и точка , принадлежит экватору шара. Невидимый участок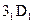 
закрыт линией видимого контура и на чертеже не изображается.
Видимым участком линии 
будет участок 
, расположенный на верхней, обращенной к наблюдателю, половине поверхности шара (сплошная толстая линия). Участок 
- невидимый (штриховая линия).
Линия 
расположена на нижней невидимой для наблюдателя половине поверхности шара, поэтому должна быть невидимой. Однако из-за наличия отверстия участок 
этой линии будет видимым (сплошная толстая линия). Участок 
- невидимый (штриховая линия).
Участк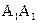и 
и 
ребер отверстия – невидимые (штриховая линия), так как расположены внутри шара.
Горизонтальный очерк шара на участке 
отсутствует из-за наличия отверстия, поэтому изображается сплошной тонкой линией. Остальная часть горизонтального очерка шара изображается сплошной толстой линией.
Проверяем правильность определения видимости очерков заданных тел и линий пересечения на плоскости . Видимые линии очерка и видимые линии пересечения переходят одна в другую и составляют замкнутый контур, следовательно, видимость линий определена правильно.
Задание 7
Задание 7. Построить линию пересечения заданных поверхностей.
Варианты задания 6 представлены в табл. 4. Вариант задания (рисунок в таблице) выбирают по последней цифре учебного шифра. Под каждым рисунком имеется таблица с переменными исходными данными. Номер столбца в этой таблице выбирают по предпоследней цифре учебного шифра.
Таблица 4
Варианты задания 7
Построение линии пересечения заданных поверхностей осуществляем по схеме, приведенной в разделе 3.1. В качестве вспомогательных секущих поверхностей используем плоскости. Такой способ реализации метода посредников называется способом вспомогательных плоскостей.
Способ секущих параллельных плоскостей обычно применяют в тех случаях, когда обе пересекающиеся поверхности одновременно можно рассечь каждой из параллельных плоскостей по простейшим сечениям – по окружностям или по прямым линиям.
Последовательности выполнения задания рассмотрим на примере построения линии пересечения цилиндра и конуса (рис. 12).
Для решения этого задания на эпюре кроме горизонтальной и фронтальной проекций необходимо построить также и профильную проекцию конуса и цилиндра (в задании 7 аналогичные построения необходимо выполнить для варианта 9).
Сначала определяем опорные точки линии пересечения.
Фронтальная плоскость D является общей плоскостью симметрии обеих поверхностей. Поэтому фронтальные проекции и 
верхней точки A и нижней точки B линии пересечения находим без дополнительных построений, как точки пересечения фронтальных очерков конуса и цилиндра.
Из точек и проводим линию связи до их пересечения с горизонтальными проекциями фронтальных очерковых линий цилиндра и конуса, совпадающих с горизонтальной осевой линией. В пересечении этих линий отмечаем горизонтальные проекции 
и 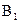верхней и нижней точек линий пересечения. Точки А и В являются также точками смены видимости линии пересечения на фронтальной плоскости проекций, на которой видимый и невидимый участки линии пересечения являются конгруэнтными фигурами.
Для построения точек 1, которые являются точками смены видимости искомой линии пересечения на плоскости 
, проводим горизонтальную вспомогательную секущую плоскость 
, проходящую через ось цилиндра. Эта плоскость пересекает конус по параллели 
- окружности радиуса 
, а поверхность цилиндра по образующим 
, фронтальные проекции которых совпадают с осью цилиндра, а горизонтальные проекции, являются горизонтальными очерковыми образующими цилиндра. В пересечении линий 
и 
отмечаем точки 
. Для построения фронтальных проекций 12 точек 1 из точек 11 проводим линию связи до пересечения со следом 
.
Рис. 12 Пример выполнения задания 7
Построение промежуточных точек 2 и 3 осуществляем по аналогичной схеме. Например, точки 2 строим с помощью вспомогательной плоскости 
, которая пересекает конус по параллели 
радиуса 
, а цилиндр по образующим 
и т. д. по схеме.
Целесообразно вспомогательные плоскости, с помощью которых строят промежуточные точки, располагать симметрично относительно оси цилиндра. В этом случае сокращается количество дополнительных построений.
Полученные точки соединяем лекальной кривой с учетом видимости. Порядок соединения точек определяем на фронтальной плоскости проекций – A®2®1®3®B. На фронтальной плоскости проекций линия 
является видимой (сплошная толстая линия). На горизонтальной плоскости проекций видимым участком линии будет участок, расположенный на верхней обращенной к наблюдателю поверхности цилиндра - 
. Участок 
- невидимый (штриховая линия).
На фронтальной плоскости проекций участок 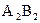левой образующей конуса расположен внутри цилиндра, поэтому изображается сплошной тонкой линией. Остальные линии фронтального очерка – сплошные толстые.
На горизонтальной плоскости проекций линией невидимого контура (штриховой) изображаются участки окружности основания конуса, закрытые цилиндром. Остальные линии горизонтального очерка – сплошные толстые.
На каждой из плоскостей проекций видимые линии очерков тел и видимые линии пересечения переходят одна в другую и составляют замкнутый контур. Следовательно, видимость определена правильно.
Рекомендуемая литература
1. Павлова А. А. Начертательная геометрия: учеб. для вузов. – М.: Изд. центр ВЛАДОС, 2008.
2. Гордон В. О., Семенцов-Огиевский М. А. Курс начертательной геометрии: уч. пос.; под ред. Ю. Б. Иванова. – М.: Наука, 2005.
3. Начертательная геометрия: учеб. для строит. спец. вузов /Под ред. Н. Н. Крылова. – М.: Высшая школа, 2000.
4. Фролов С. А. Сборник задач по начертательной геометрии: уч. пос. – СПб. – М. – Краснодар.: Изд. "Лань", 2008.
5. Зайцев В. В. Тексты лекций по начертательной геометрии для дистанционного обучения: уч. пос. / В. В. Зайцев, С. А. Синицын, В. И. Тарлыков, А. В. Шапошников; под ред. д-р техн. наук, проф. С. А. Синицына. – М.: МИИТ, 2011. – 92с.
6. Швайгер А. М. Начертательная геометрия: Компьютерный конспект лекций по начертательной геометрии. Интернет издание: http://cnit.susu.ru/alexandr.html
