Основные метрические задачи (эпюр 2)

Метрическими называются задачи, связанные с измерением расстояний и углов. В них определяются действительные величины и форма геометрических фигур, расстояния между ними и другие характеристики по их метрически искаженным проекциям. Решение метрических задач основано на том, что геометрическая фигура, принадлежащая плоскости, параллельной плоскости проекций, проецируется на нее в конгруэнтную ей фигуру (см. инварианты параллельного проецирования).

Поэтому при решении метрических задач широко используются способы преобразования комплексного чертежа, а также теоретические положения, изложенные в теме "Взаимно перпендикулярные прямые и плоскости".

Здесь рассматриваются задания 3, 4 и 5 на определение действительных величин расстояний, плоских фигур и углов.

Варианты заданий приведены в таблице 2. Номер варианта определяем по последней цифре учебного шифра - из соответствующей строки таблицы выбираем координаты точек А, В, С, D, которые являются исходными для заданий 3, 4 и 5 контрольной работы.

 

Таблица 2

Координаты точек (в мм) к заданиям 3, 4, 5

Вариант	А (х, у, z)	В (х, у, z)	С (х, у, z)	D (х, у, z)
	40,20,50 40,40,100 40,50,50 30,50,40 100,60,60 0,80,20 60,60,50 70,20,20 80,60,40 70,70,30	70,70,20 0,10,70 0,20,70 60,10,20 80,10,20 40,20,60 40,20,0 50,70,70 50,80,70 60,20,70	0,40,10 70,20,40 30,80,90 0,30,10 60,20,70 50,50,0 10,80,20 80,40,10 30,10,30 10,60,10	0,80,50 0,50,20 0,70,30 50,40,0 30,70,20 0,30,10 0,40,70 30,10,50 70,20,60 30,80,60

 

Задания 3, 4 и 5 выполняются в масштабе 1:1 и компонуются на формате А3. Пример выполнения эпюра №2 приведен на рис.5.

Если исходные данные затрудняют компоновку всех трех заданий на одном формате А3, то любое из заданий может быть выполнено на отдельном формате А4 или А3.

Рис. 5. Пример выполнения эпюра №2

ЗАДАНИЕ 3

Задание 3.Даны координаты вершин пирамиды. Определить расстояние от вершины D до противоположной грани ABC.

 

Как известно, расстояние от точки до плоскости измеряется величиной перпендикуляра, опущенного из точки на заданную плоскость. Это расстояние проецируется на какую-либо плоскость проекций в натуральную величину, если заданная плоскость перпендикулярна к плоскости проекций и, следовательно, перпендикуляр к заданной плоскости – параллелен этой плоскости проекций. Такого положения перпендикуляра относительно плоскости проекций можно добиться, преобразуя чертеж, например, способом замены плоскостей проекций.

Таким образом, решение задачи состоит из двух этапов. Сначала на основании теоремы о перпендикулярности прямой и плоскости и теоремы о проецировании прямого угла из вершины D проводим проекции перпендикуляра к плоскости грани ABC (горизонтальная проекция перпендикуляра - перпендикулярна горизонтальной проекции горизонтали плоскости, фронтальная проекция перпендикуляра – перпендикулярна фронтальной проекции фронтали плоскости). Затем способом замены плоскостей проекций определяем точку К пересечения перпендикуляра с этой гранью и его истинную величину.

Последовательность решения задания следующая.

На эпюре по заданным координатам (см. таблицу 2) строим пирамиду ABCD см. рис.6.

 

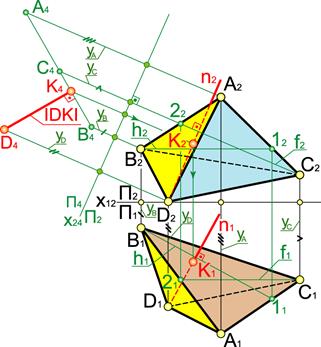Рис.6. Пример выполнения задания 3

 

Строим одну из горизонталей плоскости грани ABС. Чтобы не вводить на эпюре лишних обозначений, эту горизонталь h ( проводим через вершину В (в каждом конкретном случае это может быть любая из вершин треугольника). На основании теоремы о проецировании прямого угла через т. проводим горизонтальную проекцию перпендикуляра перпендикулярно горизонтальной проекции горизонтали - .

Строим одну из фронталей плоскости грани ABС. Чтобы не вводить на эпюре лишних обозначений, эту фронталь f проводим через вершину C. На основании теоремы о проецировании прямого угла через т. проводим фронтальную проекцию перпендикуляра перпендикулярно фронтальной проекции фронтали - . Перпендикуляр n(, ) построен.

Определим точку К пересечения перпендикуляра n с плоскостью грани АВС, а также истинную величину искомого расстояния DK способом замены плоскостей проекций. Для этого вместо плоскости ведем новую плоскость . Плоскость в пространстве располагаем перпендикулярно плоскости грани АВС (перпендикулярно фронтали f грани АВС) и, соответственно, перпендикулярно плоскости . В этом случае на эпюре новую ось проекций располагаем перпендикулярно фронтальной проекции фронтали на произвольном расстоянии от фронтальной проекции пирамиды.

Строим проекции точки D - и грани АВС - на плоскости проекций . Для этого на перпендикулярах к новой оси проекций 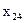, проведенных через фронтальные проекции точек A₂, B₂, C₂ и D₂, откладываем координаты .

Проекция грани АВС на плоскости выродилась в прямую линию , так как плоскость АВС стала проецирующей - перпендикулярной .

Из точки опускаем перпендикуляр на прямую и определяем точку пересечения перпендикуляра n с гранью АВС. Проекция перпендикуляра располагается параллельно плоскости , так как || 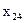, поэтому её длина равна искомому расстоянию от вершины D до плоскости грани АВС.

По линиям проекционной связи, строим проекции т. K на плоскостях проекций и (на рис.6 эти построения показаны стрелками).

Обводим чертеж с учетом видимости элементов и толщины линий.

Задание 4

Задание 4. Найти длину ребра АВ и угол между ребрами АВ и АD

 

В качестве исходных данных имеем плоскость, заданную плоской фигурой - треугольником ABD. Очевидно, что элементы треугольника проецируются без искажения величины, если его плоскость будет параллельна одной из плоскостей проекций. Таким образом, требуется преобразовать плоскость общего положения в плоскость уровня.

Подобное преобразование можно выполнить способом замены плоскостей проекций или способом вращения (при выполнении задания можно пользоваться любым из указанных способов).

В примере выполнения эпюра №2 на рис. 5 при решении задания 4 использован способ замены плоскостей проекций.

В данном случае воспользуемся способом вращения вокруг проецирующих прямых без указания осей вращения. Если вращать плоскую фигуру вокруг оси, перпендикулярной к плоскости проекций, то её проекция на эту плоскость проекций не изменяется ни по виду, ни по величине – меняется лишь положение этой проекции относительно оси проекций. Все точки другой проекции на плоскости, параллельной оси вращения, перемещаются по прямым линиям, параллельным оси проекций, и проекция в общем случае изменяется и по форме и по величине. Пользуясь этими свойствами, можно не задавать оси вращения и не определять радиусы вращения точек; достаточно лишь, не изменяя вида и величины одной из проекций фигуры, переместить эту проекцию в требуемое положение, а затем построить другую проекцию, как указано выше.

Последовательность выполнения задания следующая.

На эпюре (рис.7) по заданным координатам (см. таблицу 2) строим исходные данные – отрезки AB (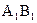; 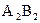) и AD (). Соединяем точки B и D линией вспомогательных построений. В результате получаем треугольник ABD.

Очевидно, что треугольник АВD проецируется без искажения величины в том случае, когда его плоскость будет параллельна одной из плоскостей проекции. При этом плоскость треугольника будет перпендикулярна другой плоскости проекций.

Преобразование плоскости общего положения в плоскость уровня осуществляется в две стадии (двумя последовательными вращениями). На первой стадии вращением вокруг оси, перпендикулярной, например, горизонтальной плоскости проекций (без указания её положения), переместим треугольник ABD в положение, перпендикулярное фронтальной плоскости проекций. В этом случае горизонталь плоскости треугольника ABD необходимо расположить перпендикулярно плоскости проекций . При таком перемещении горизонтальная проекция треугольника , оставаясь конгруэнтной самой себе, займет положение , при котором .

Рис.7 Пример выполнения задания 4

 

Проведем на чертеже указанное преобразование.

Строим одну из горизонталей h () плоскости треугольника ABD. Чтобы не вводить лишних обозначений, горизонталь проводим через вершину D.

На свободном поле чертежа справа проводим прямую перпендикулярную оси проекций . На этой прямой произвольно отмечаем т. и на расстоянии, равном - точку . Используя эти точки, методом триангуляции (треугольников) строим треугольник , равный треугольнику .

По линиям проекционной связи строим фронтальную проекцию треугольника, которая выродилась в прямую линию.

Следующим вращением вокруг оси, перпендикулярной плоскости проекций и проходящей через точку В, перемещаем плоскость треугольника ABD в положение, параллельное плоскости проекций . Для этого фронтальную проекцию треугольника располагаем параллельно оси проекций - ( || ).

По линиям проекционной связи строим горизонтальную проекцию , которая представляет треугольник ABD в истинную величину. На этой проекции ( |AB|) и угол есть истинная величина угла между ребрами AB и AD - (φ=AB^AD).

Обводим чертеж с учетом толщины линий.

 

Задание 5

Задание 5. Определить угол между гранями ABC и ABD.

 

Линейный угол двугранного угла между плоскостями граней ABC и ABD измеряется в плоскости, перпендикулярной ребру AB двугранного угла. Отсюда следует, что двугранный угол необходимо установить в пространстве так, чтобы ребро AB стало перпендикулярным плоскости проекций. В этом случае плоскости граней ABC и ABD также станут перпендикулярными этой плоскости проекций, а их проекции выродятся в два отрезка, исходящих из одной точки. Угол между этими отрезками и будет являться искомым углом между гранями ABC и ABD.

Таким образом, решение задачи сводится к преобразованию ребра AB из прямой общего положения в проецирующую прямую.

Для решения задачи используем способ замены плоскостей проекций. Преобразование прямой общего положения в проецирующую прямую осуществляется двойной заменой плоскостей проекций. Первой заменой отрезок AB преобразуем в прямую уровня и второй заменой – в проецирующую прямую.

Последовательность выполнения задания следующая.

На эпюре (рис.8) по заданным координатам (см. таблицу 2) строим два треугольника: ABC - () и ABD - (). Точки C и D соединять не нужно.

 

Рис.8. Пример выполнения задания 5

 

Преобразуем отрезок AB в прямую уровня.

Заменим старую систему взаимно перпендикулярных плоскостей проекций на новую систему также ортогональных плоскостей проекций . Плоскость в пространстве установим параллельно ребру AB. Для этого на эпюре новую ось проекций нужно расположить параллельно горизонтальной проекции ребра - || .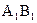

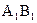Строим новые проекции точек - . При построении новых проекций точек полезно пользоваться правилом – расстояние от новой проекции точки до новой оси проекций равно расстоянию от старой изменяемой проекции точки до старой оси проекций. В нашем случае - это координаты точек (см. рис.8).

В системе плоскостей проекций отрезок AB стал параллелен плоскости П₄.

Преобразуем отрезок AB в проецирующую прямую.

Заменим плоскость плоскостью , которую в пространстве установим перпендикулярно ребру AB. В этом случае на эпюре новую ось проекций необходимо расположить перпендикулярно проекции - .

Строим новые проекции точек - . Для построения точек на плоскости проекций на линиях связи от оси проекций откладываем значения координат .

На плоскости проекция ребра AB выродилась в точку, а проекции граней ABC и ABD – в прямые линии, угол φ между которыми (рис.8) и является искомым углом.