Задания 1,2 по начертательной геометрии связаны с построением комплексного чертежа Монжа и аксонометрического чертежа (прямоугольной изометрии).
Для решения этих задач используется пирамида, заданная координатами вершин A, B, C, D (табл. 1).
Десять вариантов заданий приведены в табл.1. Номер варианта выбирают по последней цифре учебного шифра.
Таблица 1
| Вариант | A(X,Y,Z) | B(X,Y,Z) | C(X,Y,Z) | D(X,Y,Z) |
| 40,20,50 | 0,70,20 | 0,20,70 | 10,50,0 | |
| 40,40,100 | 40,100,20 | 20,80,40 | 90,60,40 | |
| 40,50,60 | 60,90,40 | 20,100,100 | 70,50,90 | |
| 30,50,40 | 80,70,40 | 50,100,40 | 40,70,80 | |
| 100,60,60 | 20,80,20 | 60,80,90 | 40,100,30 | |
| 10,80,20 | 50,20,60 | 50,70,40 | 40,100,90 | |
| 60,60,50 | 40,90,50 | 40,60,110 | 60,90,30 | |
| 70,20,20 | 50,70,70 | 50,30,10 | 20,30,70 | |
| 80,60,40 | 100,50,50 | 50,60,80 | 80,100,70 | |
| 70,70,30 | 60,50,80 | 30,50,80 | 80,40,10 |
Координаты точек (в мм) к заданиям 1, 2
Задания 1, 2 выполняются в масштабе 1:1 и компонуются на одном формате А3 размером (420Х297)мм. согласно рис. 2.
ЗАДАНИЕ 1
Задание 1. Даны координаты вершин пирамиды. Построить горизонтальную и фронтальную проекции пирамиды, определить видимость ребер.
Последовательность выполнения задания 1 представлена на рис. 3.
На комплексном чертеже задаем систему координат (рис. 3, а). Обозначаем оси координат (x,y,z) и плоскости проекций (П1,П2).
По данным таблицы 1 строим горизонтальную и фронтальную проекции четырех точек (рис. 3, б) –A (A1,A2); B(B1,B2); C(C1,C2); D(D1,D2). Индекс «два» используют для обозначения проекций на фронтальную плоскость П2, «один» - на горизонтальную плоскость П1. Если в конкретном варианте задано отрицательное значение координаты, то оно должно быть отложено от нуля в противоположном направлении (-x,-y,-z), рис. 3, а.
На рис. 3, б показано построение точки А. Построение остальных точек осуществляется по аналогичной схеме.
Одноименные проекции точек соединяем сплошными тонкими линиями (рис. 3, в).
Определяем видимость ребер пирамиды. Замкнутая ломаная линия A1C1B1 называется горизонтальным очерком пирамиды, а замкнутая ломаная A2C2D2B2 - фронтальным очерком. Очерки проекций всегда видимые (рис. 3, г). Видимость проекций линий, расположенных внутри очерка, определяем методом конкурирующих точек.
Существенную помощь при определении видимости могут оказать следующие правила:
1. Если внутри очерка пересекаются две линии, то одна из них видимая, а другая - невидимая;
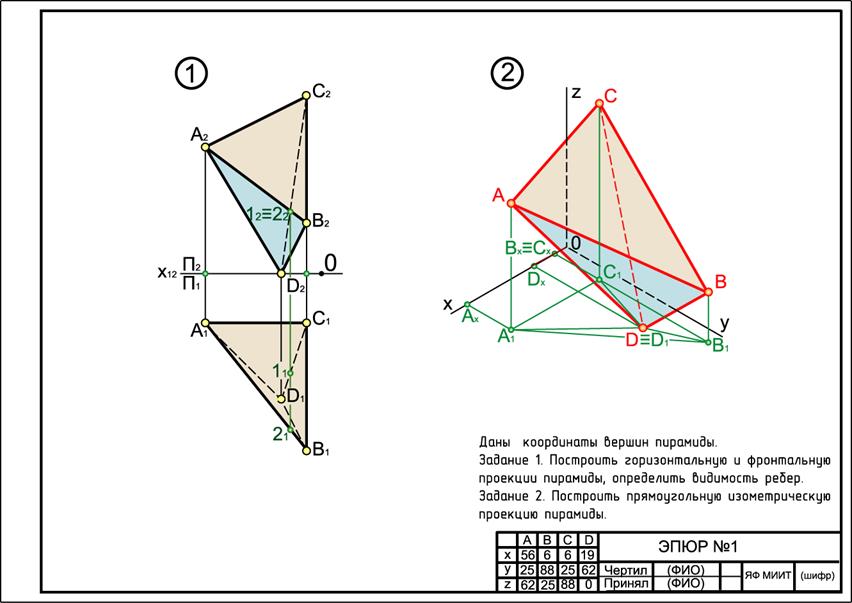
Рис. 2. Пример выполнения эпюра №1
2. Если внутри очерка пересекаются в одной точке три линии, то все три будут видимые или все три - невидимые;
3. Если последовательность букв или цифр при обходе какой-либо грани в одном направлении одинакова на обеих проекциях, то и видимость этой грани на обеих проекциях одинакова, в противном случае - разная.
Рис. 3 Последовательность выполнения задания 1.
Определим на фронтальной плоскости проекций видимость ребер AB и CD, расположенных внутри фронтального очерка пирамиды. Конкурирующие точки 1 и 2 (рис. 3, г) определяем в пересечении фронтальных проекций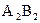 
и 
. Пусть точка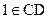 
, а точка 
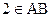. Строим горизонтальные проекции 
и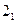 
точек 1 и 2. В нашем случае (
> 
) и впереди лежащим ребром является ребро АВ, если смотреть по стрелке А. Поэтому на фронтальной плоскости проекций ребро AB – видимое, а ребро CD - невидимое.
Определим на горизонтальной плоскости проекций видимость ребер AD, CD и BD, расположенных внутри горизонтального очерка пирамиды. Вершина D пирамиды расположена под основанием АВС пирамиды (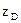
=0), если смотреть по стрелке В. Поэтому на горизонтальной плоскости проекций эта вершина невидимая и, следовательно, ребра AD, BD и CD тоже невидимые. Видимые ребра обводим сплошной основной линией, невидимые – штриховой.
Рис. 3, г является первым готовым фрагментом эпюра №1 (см. рис. 2).
ЗАДАНИЕ 2
Задание 2. Даны координаты вершин пирамиды. Построить прямоугольную изометрическую проекцию пирамиды.
Последовательность выполнения задания представлена на рис. 4.
Изображаем пространственную систему координат в прямоугольной изометрии (рис. 4, а) с осями, направленными друг относительно друга под углом 1200 (см. ГОСТ – 2.317-2011).
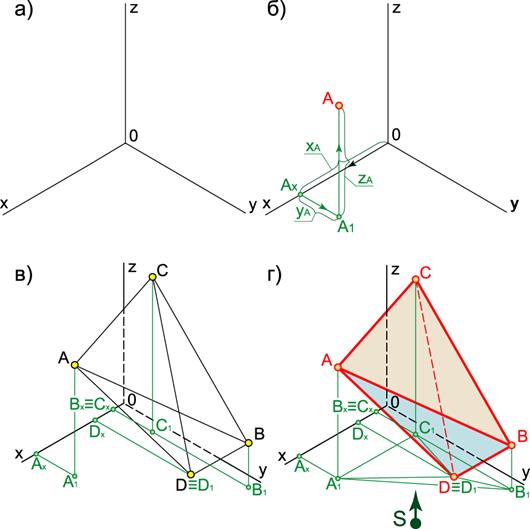
Рис. 4 Последовательность выполнения задания 2
В прямоугольной изометрии все три коэффициента искажения по аксонометрическим осям одинаковы и равны 0,82. Обычно для упрощения построений в практической изометрии эти коэффициенты полагают равными 1, т.е. отрезки, параллельные аксонометрическим осям, откладываем действительной длины.
Строим единственную проекцию каждой точки по схеме, представленной на рис. 4, б. Для этого от начала координат 0 по оси х откладываем отрезок, равный значению координаты х т.А. Получаем точку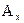 
. Из точки 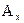проводим прямую, параллельную оси y, и на ней откладываем отрезок, равный значению координаты y т.А, получаем точку 
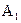. Точка 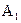является проекцией т. А на координатную плоскость x0y. В дальнейшем т. 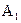будем называть вторичной проекцией т. А. Из точки 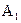проводим прямую параллельную оси z, на которой откладываем отрезок, равный значению координаты z т. А. В результате в конце аксонометрической ломаной получаем изометрическую проекцию т.А. Остальные точки строим по аналогичной схеме.
Полученные точки соединяем каждую с каждой (рис. 4, в) и определяем видимость ребер. Очерк ACBD пирамиды является видимым (рис. 4, г). Для определения видимости ребер AB и CD, расположенных внутри очерка, строим проекцию пирамиды на координатную плоскость x0y (вторичную проекцию) -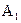 
.
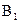
Наблюдатель располагается перед системой координат в точке S; направление взгляда показано стрелкой. По рисунку видим, что проекция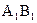 
расположена впереди, т.е. ближе к наблюдателю, а проекция сзади. Следовательно и на наглядном изображении ребро АВ расположено ближе к наблюдателю и является видимым, а ребро CD - невидимым. Для определения видимости ребер можно также воспользоваться комплексным чертежом пирамиды (рис. 3, г)
Рис. 4, г может быть перенесен на формат в качестве второго задания. Здесь же необходимо показать тонкими линиями построение вершин пирамиды.
