Задачи, приводящие к обыкновенным дифференциальным уравнениям (ОДУ).
К понятию обыкновенного дифференциального уравнения приводят физические и геометрические задачи.
Физическая задача. Найти закон движения материальной точки под действием силы тяжести.
Решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения.
Уравнение, описывающее свободные колебания материальной точки в среде без сопротивления является ОДУ и может быть записано в виде: 
2. Определение ОДУ. Порядок ОДУ. Задача Коши для уравнения n -ого порядка. Общие и частные решения.
Дифференциальным уравнением называется уравнение, связывающее независимую переменную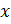 
, искомую функцию 
и ее производные 
, т.е. уравнение вида 
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Задача Коши для любого дифференциального уравнения n -го порядка
.
Общим решением ДУ 
называется ф – ия 
, зависящая от одной произвольной постоянной С.
Частным решением ДУ называется решение, получаемое из общего решения при каком – либо определенном значении С.
Геометрический смысл уравнения 1-ого порядка. ОДУ 1-ого порядка, его геометрический смысл. Изоклины.
Общий вид ДУ 1 – ого порядка: 
. => . Уравнение в каждой точке 
области D, в которой задана функция 
, определяет 
- угловой коэффициент касательной к решению, проходящему через точку 
, т.е. направление, в котором проходит решение через эту точку. (Геом. смысл)
Задачи построения интегральной кривой часто решают методом введения изоклин. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и то же направление.
4. Теорема Коши существования и единственности решения ОДУ 1-ого порядка, разрешённого относительно производной. ОДУ с разделяющимися переменными.
Пусть дано ДУ , где функция определена в некоторой области D плоскости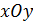 
, содержащей точку 
. Если удовлетворяет условиям:
А) – непрерывная ф-я 2 – х переменных 
в области D.
Б) имеет частную производную 
ограниченную в D, то найдется интервал 
, на котором существует единственное решение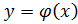 
данного уравнения, удовлетворяющее условию 
.
Уравнение, в котором коэф – ты при дифференциалах распадаются на множители, зависящие только от 
, называется ур – ем с разделяющимися переменными. Общий интеграл такого ур – ия имеет вид:
Однородные ОДУ 1-ого порядка. Приведение их к уравнениям с разделяющимися переменными.
Функция 
называется однородной ф – ией своих аргументов измерения n, если справедливо тождество 
.
Путем замены 
однородное ОДУ 1 – ого порядка приводится к ур – ию с разделяющимися переменными.
6. Уравнения вида: y’ = f [ (a1x + b1y + c1) / (a2x + b2y +c2) ].
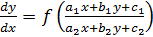если 
, то ур – ие однородное и решается с помощью замены 
. Если хоть одно с отлично от нуля, то ур – ие приводится к однородному.
Если 
, то вводим новые переменные 
, 
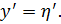
Если 
, то 
, тогда исходное ур – ие имеет вид:
, с помощью подстановки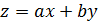 
приводим его к ур – ию с разделяющимися переменными.
