Лабораторная работа включает следующие этапы:
· постановку задачи;
· ознакомление с порядком выполнения работы в диалоговой системе STADIA;
· выполнение расчетов индивидуальных задач;
· подготовку письменного отчета;
· защиту лабораторной работы.
Постановка задачи
По выборочным значениям вычислить точечные и интервальные оценки числовых характеристик положения, вариации и формы генеральной совокупности (среднюю арифметическую, ошибку среднего, характеризующую точность вычисленного среднего значения, оценку дисперсии, оценку среднего квадратичного отклонения, ошибку среднего квадратичного отклонения (характеристика точности найденного значения), оценки асимметрии и эксцесса, доверительные интервалы для генеральной средней и дисперсии и др.). Проанализировать полученные результаты. Сделать выводы о распределении генеральной совокупности.
Примечания
1. Данная лабораторная работа выполняется с помощью процедуры "Описательная статистика" в диалоговой системе STADIA.
2. Построение доверительных интервалов в программе предполагает, что выборка сделана из нормального распределения или же объем выборки достаточно велик, что говорит об асимптотическом приближении распределения к нормальному.
3. В последующих работах при нахождении значимости Р полученных оценок в системе STADIA используются приближенные формулы, дающие хорошие результаты (точность до трех значащих цифр) для больших выборок, включающих более 30 элементов. Кроме того, эти формулы удовлетворительно аппроксимируют соответствующие статистические распределения только в области критических значений уровня значимости 0.001<Р<0.1. В области других значений Р они могут давать весьма приблизительные оценки, которые могут даже быть больше 1. Однако это не является серьезным недостатком - при получении больших или малых значений Р совершенно ясно, можно или нельзя принимать нулевую гипотезу.
4. В системе STADIA автоматически заложен уровень значимости 0,05, однако, при необходимости это значение можно поменять. Под пунктом "Окна" в строке основного меню выбираем опцию "Установки". При этом появляется окно для установки параметров электронной таблицы и результатов (рисунок 1).
Рисунок 1– Окно параметров установки
В поле напротив "Уровень значимости =" введите нужное значение.
5. Дробные числа в системе STADIA вводятся через точку.
Порядок выполнения работы в диалоговой
Системе STADIA
Запустить программную систему STADIA дважды щелкнув указателем мыши по ярлыку 
на рабочем столе вашего компьютера. На экране монитора появится электронная таблица системы STADIA (рисунок 2).
Рисунок 2 – Электронная таблица системы STADIA
Для ввода данных в электронную таблицу необходимо сделать активной первую клетку (левую верхнюю), щелкнув по ней указателем мыши или используя клавиши движения курсора. Набрать значение. Переход к следующей позиции осуществляется нажатием клавиши Enter. Каждую выборочную совокупность ввести в отдельный столбец.
Запись содержимого активной страницы осуществляется с помощью команды "Сохранить" из пункта основного меню "Файлы", а также по нажатию на клавишу F4 или же на кнопку 
на экранной линейке. Бланк сохранения данных представлен на рисунке 3. В левом окне представлены файлы текущего каталога, в правом окне - дерево каталогов выбранного диска. Переключатель дисков находится внизу бланка. Наберите имя файла (без пробелов и знаков препинания, не более 8 знаков) в поле ниже кнопки 
. Для сохранения нажмите на эту кнопку или на клавишу Enter.
Рисунок 3 – Типовой бланк сохранения файла
Для проведения статистического анализа вызываем меню статистических методов - пункт "Статистика" в верхней командной строке или клавиша F9 (рисунок 4).
Рисунок 4– Бланк меню статистических методов
В этом меню выбираем кнопку "Описательная статистика". После этого на экране появится новая страничка системы STADIA - Результаты и типовой бланк выбора переменных из электронной таблицы для анализа (рисунок 5).
Рисунок 5 – Типовой бланк выбора переменных для анализа
Бланк содержит:
· слева окно со списком всех переменных электронной таблицы;
· справа окно для выбранных переменных.
Между окнами находятся кнопки переноса переменных из одного окна в другое. Для формирования списка переменных для анализа необходимо выделить нужную переменную или группу переменных в левом окне и нажать стрелку вправо. Для переноса всех переменных можно использовать кнопку "Все". После завершения формирования списка анализируемых переменных следует нажать кнопку "Утвердить" (дублируется клавишей Enter). Кнопка "Отменить" (дублируется Esc) отменяет бланк выбора переменных.
Вывод результатов происходит после выбора переменных. Она включает следующие выборочные характеристики: название переменой, размер выборки, диапазон значений, выборочное среднее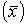 
, ошибка вычисления выборочного среднего 
, выборочная несмещенная оценка дисперсии и стандартное отклонение (S2 и S).
Далее по подтверждению (рисунок 6) может быть выдана дополнительная статистика:
- оценка медианы;
- квантили;
- размах 95% доверительного интервала для среднего (dМ);
- границы 95% интервала для дисперсии (S1, S2);
- ошибка стандартного отклонения
;
- оценки асимметрии и эксцесса с уровнем значимости Р нулевой гипотезы об отсутствии различий выборочного распределения по каждому из коэффициентов
Рисунок 6 – Страничка результатов
Затем по подтверждению (рисунок 7), вычисленные средние значения и стандартные отклонения могут быть сохранены в электронной таблице для дальнейшего анализа.
Рисунок 7
В итоге по нашим данным получили следующую описательную статистику:
Рисунок 8 – Результаты описательной статистики
Вернуться из текстового редактора в электронную таблицу можно при активизации соответствующей страницы с помощью закладки [Dat], расположенной внизу.
Анализ результатов
Для наиболее полного анализа результатов рекомендуется вспомнить материал общей теории статистики.
Приведем пример анализа переменой х1.
Основной целью проводимого анализа является получение общих и числовых характеристик случайной величины х1 по выборочным данным.
На основании полученных результатов можно заключить, что значения переменной сгруппированы вокруг выборочной средней 68,2 (оценка генеральной средней), при этом оценка медианы равна 69. Поскольку оценка средней незначительно отличается от оценки медианы можно предположить, что распределение случайной величины х1 близко к симметричному. Для проверки этого предположения необходимо проанализировать коэффициент асимметрии.
Оценкой коэффициента асимметрии генеральной совокупности является коэффициент асимметрии выборочной совокупности. Эта оценка является несмещенной и состоятельной. Аs*= -0,126. Коэффициент близок к нулю, следовательно, можно предположить, что распределение является симметричным (в дальнейшем мы будем пользоваться значимостью данного коэффициента).
Для характеристики вариации признака используем размах вариации, оценки дисперсии, среднего квадратического отклонения и квартильные отклонения. В нашем случае указан диапазон значений выборочной совокупности: минимальное значение - 56, максимальное значение - 79, таким образом, размах вариации равен 79-56=23. Но оценка размаха вариации приемлема только для однородных совокупностей, поэтому целесообразнее использовать другие показатели, которые характеризуют отклонение значений признака отдельных единиц совокупности от средней величины. Для переменной х1 оценка дисперсии равна 34.1, соответственно оценка среднего квадратического отклонения 5,84. Данная оценка дисперсии генеральной совокупности является несмещенной и состоятельной. Таким образом, мы можем заключить, опираясь на правило "трех сигм", что основная масса единиц совокупности х1, расположена вокруг среднего значения в интервале 68,2±3·5,84.
Если в качестве показателя центра распределения используется медиана, то для характеристики вариации признака в совокупности можно применить процентные точки и в частности так называемые квартильные отклонения. Этот показатель можно также применить вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений. Мы получили Q1=64, Q3=71.
Для оценки эксцесса генеральной совокупности возьмем выборочный эксцесс. Она также является несмещенной и состоятельной. Е[x1]=2,54 Близость оценки эксцесса к 3, а асимметрии к 0 говорит о близости распределения к нормальному. Поэтому имеет смысл обсудить интервальные оценки генеральных параметров.
Получены доверительные интервалы с вероятностью 0,95 "накрывающие" неизвестные значения среднего и дисперсии. Отметим, что поскольку выборка у нас достаточно велика (45 значений), то статистики, применяемые для нахождения доверительных интервалов, имеют нормальный закон распределения. На основании представленных результатов можно заключить, что распределение случайной величины х1 является близким к нормальному или нормальным (на основании оценок эксцесса и асимметрии) и среднее значение генеральной совокупности заключено в интервале 68,2±4,32. Доверительный интервал для дисперсии (26,2; 236).
Отчет должен содержать следующее:
· постановку задачи с вариантом выборок;
· результаты компьютерной обработки данных;
· анализ полученных результатов по каждой переменной;
· выводы, содержащие характеристику генеральной совокупности.
Контрольные вопросы
1. Что называется генеральной совокупностью?
2. Что называется выборочной совокупностью?
3. Постановка задачи статистического оценивания.
4. Дать определение точечной оценки.
5. Какую оценку называют несмещенной? эффективной? состоятельной?
6. Как определяется выборочное среднее?
7. Как определить несмещенную и состоятельную оценку математического ожидания генеральной совокупности?
8. Дать определение выборочной дисперсии. Каким свойством оценок она обладает?
9. Как определить несмещенную оценку дисперсии генеральной совокупности?
10. Дать определение эффективной оценки генеральной дисперсии.
11. Как определяются мода и медиана совокупности?
12. Понятие интервальной оценки неизвестного параметра генеральной совокупности.
13. Как найти интервальную оценку для генеральной средней нормально распределенной совокупности при известном среднем квадратическом отклонении?
14. Как найти интервальную оценку для генеральной средней нормально распределенной совокупности при неизвестном среднем квадратическом отклонении?
15. Каким образом определяется интервальная оценка среднего квадратического и дисперсии нормально распределенной генеральной совокупности?
16. Что характеризует асимметрия. Как определяется оценка асимметрии генеральной совокупности?
17. Каким образом оценивается эксцесс генеральной совокупности? Характеристикой чего является этот параметр?
Литература:
1 Сытько В.В. Теоретическая метрология. 1. Физические величины и их
измерение. Мн., - 1998.
2 Сергеев А.Г., Крохин В.В. Метрология: Учебное пособие для вузов. - М.:
Логос, 2001.
3 Маркин Н.С. Введение в метрологию. - М.: Издательство стандартов, 1991.
4 Тойберг П. Оценка точности результатов измерений. - М.: Энергоатомиздат,
1988.
5 Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений.
- М.: Энергоатомиздат, 1990.
