Все моменты представляют собой некоторые средние значения, причем если усредняются величины, отсчитываемые от начала координат, то моменты называют начальными, а если от центра распределения, то центральными. Начальные и центральные моменты r-го порядка определяются соответственно по формулам
; 
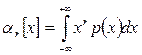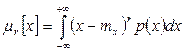
Нулевой начальный момент равен единице. Он используется для задания условия нормирования плотности распределения:
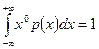
Также с помощью начального момента нулевого порядка вводится понятие медианы распределения. Первый начальный момент – математическое ожидание mх случайной величины:
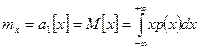
Для результатов измерений оно представляет собой оценку истинного значения измеряемой величины. Начальные и центральные моменты случайной погрешности совпадают между собой и с центральными моментами результатов измерений: аг[Δ] = μr[Δ] = μr[х], поскольку mх случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю. Важное значение имеет второй центральный момент
,
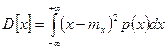называемый дисперсией и являющийся характеристикой рассеивания случайной величины относительно математического ожидания. Значительно чаще в качестве меры рассеивания используется среднее квадратическое отклонение
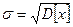
имеющее такую же размерность, как и математическое ожидание. Для примера на рис. 5.1 показан вид нормального распределения при различных значениях СКО. Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют важные черты распределения: положение центра и степень разбросанности результатов относительно него. Для более подробного описания распределения используются моменты более высоких порядков.
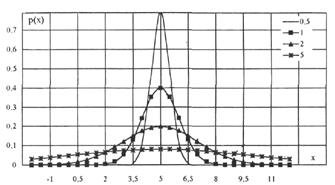
Рисунок 1 – Вид нормального распределения при Xц = 5 и СКО = 0,5; 1; 2 и 5
Третий центральный момент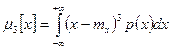 
служит характеристикой асимметрии, или скошенности распределения. С его использованием вводится коэффициент асимметрии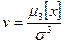 
. Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на рис. 5.2,а.
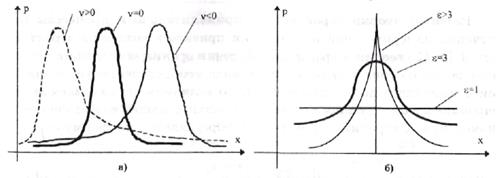
Рисунок 2 – Вид дифференциальной функции распределения при различных значениях
коэффициента асимметрии (а) и эксцесса (б)
Четвертый центральный момент
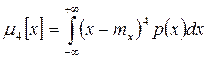
служит для характеристики плоско– или островершинности распределения. Эти свойства описываются с помощью эксцесса
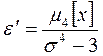
Значения коэффициента ε' лежат в диапазоне от –2 до ∞. Для нормального распределения он равен 0. Чаще эксцесс задается формулой
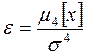
Его значения лежат в диапазоне от 1 до ∞. Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на рис. 5.2, б.
Для удобства часто используют контрэксцесс
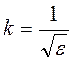
Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577.