Краткие теоретические сведения. Оценивание параметров генеральной совокупности

Лабораторная работа № 4

Оценивание параметров генеральной совокупности

в диалоговой системе «STADIA»

Цель работы: освоить методику оценивания точечных и интервальных параметров генеральной совокупности с помощью современных программных продуктов.

Приборы и принадлежности: Персональный компьютер.

 

Краткие теоретические сведения

Точечные оценки параметров распределения. На прак­тике все результаты измерений и случайные погрешности являют­ся величинами дискретными, т.е. величинами x_i возможные зна­чения которых отделимы друг от друга и поддаются счету. При использовании дискретных случайных величин возникает задача нахождения точечных оценок параметров их функций распределе­ния на основании выборок – ряда значений х_i принимаемых слу­чайной величиной х в n независимых опытах. Используемая вы­борка должна быть репрезентативной (представительной), т.е. должна достаточно хорошо представлять пропорции генеральной совокупности.

Оценка параметра называется точечной, если она выражается одним числом. Задача нахождения точечных оценок – частный случай статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выбор­ки. Любая точечная оценка, вычисленная на основании опытных данных, является их функцией и поэтому сама должна представлять собой случайную величину с распределением, зависящим от распределения исходной случайной величины, в том числе от самого оцениваемого параметра и от числа опытов n.

Точечные оценки могут быть состоятельными, несмещенными и эффективными.

Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к ис­тинному значению числовой характеристики.

Несмещенной на­зывается оценка, математическое ожидание которой равно оце­ниваемой числовой характеристике (параметру).

Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра, т.е. наиболее эффективной счи­тают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию.

Требование несмещенности на прак­тике не всегда целесообразно, так как оценка с небольшим сме­щением и малой дисперсией может оказаться предпочтительнее несмещенной оценки с большой дисперсией. На практике не все­гда удается удовлетворить одновременно все три этих требова­ния, однако выбору оценки должен предшествовать ее критиче­ский анализ со всех перечисленных точек зрения.

Наиболее распространенным методом получения оценок явля­ется, метод наибольшего (максимального) правдоподобия, теоретически обоснованный математиком Р. Фишером, который приводит к асимптотически несмещенным и эффективным оценкам с при­ближенно нормальным распределением. Среди других методов мож­но назвать методы моментов и наименьших квадратов.

Точечной оценкой математического ожидания результата измерений является среднее арифметическое значение измеряемой величины

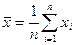(1)

При любом законе распределения оно является состоятельной и несмещенной оценкой, а также наиболее эффективной по крите­рию наименьших квадратов.

Точечная оценка дисперсии, определяемая по формуле

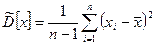(2)

является несмещенной и состоятельной.

Среднеквадратическое отклонение случайной величины х определяется как корень квадрат­ный из дисперсии. Соответственно его оценка может быть найдена путем извлечения корня из оценки дисперсии. Однако эта опера­ция является нелинейной процедурой, приводящей к смещенности получаемой таким образом оценки. Для исправления оценки СКО вводят поправочный множитель k(n), зависящий от числа наблю­дений n. Он изменяется от k(3)=1,13 до k(∞) = 1,03. Оценка сред­него квадратического отклонения

Полученные оценки математического ожидания и СКО являются случайными величи­нами. Это проявляется в том, что при повторениях серий из n наблюдений каждый раз будут получаться различные оценк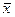и и 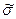. Рассеяние этих оценок целесообразно оценивать с помощью СКО и S_σ. Оценка СКО среднего арифметического значения

(3)

Оценка СКО среднего квадратического отклонения

Отсюда следует, что относительная погрешность определения СКО может быть оценена как

Она зависит только от эксцесса и числа наблюдений в выборке и не зависит от СКО, т.е. той точности, с которой производятся измерения. Ввиду того, что большое число измерений проводит­ся относительно редко, погрешность определения, а может быть весьма существенной. В любом случае она больше погрешности из-за смещенности оценки, обусловленной извлечением квадрат­ного корня и устраняемой поправочным множителем k(n). В связи с этим на практике пренебрегают учетом смещенности оценки СКО отдельных наблюдений и определяют его по формуле

(4)

т.е. считают k(n)=1.

Иногда оказывается удобнее использовать следующие формулы для расчета оценок СКО отдельных наблюдений и результата измерения:

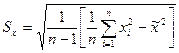; (5)

Точечные оценки других параметров распределений использу­ются значительно реже. Оценки коэффициента асимметрии и экс­цесса находятся по формулам

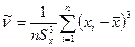; (6)

(7)

Определение рассеяния оценок коэффициента асимметрии и экс­цесса описывается различными формулами в зависимости от вида распределения.

Оценка с помощью интервалов. Рассмотренные точечные оценки параметров распределения да­ют оценку в виде числа, наиболее близкого к значению неизвест­ного параметра. Такие оценки используют только при большом числе измерений. Чем меньше объем выборки, тем легче допус­тить ошибку при выборе параметра. Для практики важно не толь­ко получить точечную оценку, но и определить интервал, называе­мый доверительным, между границами которого с заданной дове­рительной вероятностью

где q – уровень значимости; х_н, x_в – нижняя и верхняя границы интервала, находится истинное значение оцениваемого параметра.

В общем случае доверительные интервалы можно строить на основе неравенства Чебышева. При любом законе распределения случайной величины, обладающей моментами первых двух поряд­ков, верхняя граница вероятности попадания отклонения случай­ной величины х от центра распределения х_ц интервал tS_x описы­вается неравенством Чебышевa

где S_х – оценка СКО распределения; t– положительное число.

Для нахождения доверительного интервала не требуется знать закон распределения результатов наблюдений, но нужно знать оцен­ку СКО. Полученные с помощью неравенства Чебышева интервалы оказываются слишком широкими для практики. Так, доверитель­ной вероятности 0,9 для многих законов распределений соответст­вует доверительный интервал 1,6S_x. Неравенство Чебышева дает в данном случае 3,16S_x. В связи с этим оно не получило широкого распространения.

В метрологической практике используют главным образом квантильные оценки доверительного интервала. Под 100P-процентным квантилем х_р понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна Р%. Иначе говоря, квантиль – это значение случайной величины (погрешности) с заданной доверительной вероятностью Р. Напри­мер, медиана распределения является 50%-иым квантилем х_0,5.

На практике 25- и 75%-ный квантили принято называть сгиба­ми, или квантилями распределения. Между ними заключено 50% всех возможных значений случайной величины, а остальные 50% лежат вне их. Интервал значений случайной величины х между х_0,05и х_0,95 охватывает 90% всех ее возможных значений и называ­ется интерквантильным промежутком с 90%-ной вероятностью. Его протяженность равна d_0,9= х_0,95 – х_0,05.

На основании такого подхода вводится понятие квантильных значений погрешности, т.е. значений погрешности с заданной до­верительной вероятностью Р – границ интервала неопределенно­сти ±Δ_Д = ±(х_p – х_1–p)/2 = ±d_p/2. На его протяженности встречается Р% значений случайной величины (погрешности), а q = (1–Р)% общего их числа остаются за пределами этого интервала.

Для получения интервальной оценки нормально распределен­ной случайной величины необходимо:

• определить точечную оценку МО и СКО S_x случайной вели­чины по формулам (6.8) и (6.11) соответственно;

• выбрать доверительную вероятность Р из рекомендуемого ря­да значений 0,90; 0,95; 0,99;

• найти верхнюю х_B и нижнюю х_H границы в соответствии с уравнениями

и

 

полученными с учетом (6.1). Значения х_н и х_в определяются из таблиц значений интегральной функции распределения F(t) или функции Лапласа Ф(t).

Полученный доверительный интервал удовлетворяет условию

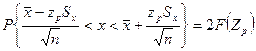
где n – число измеренных значений; z_Р – аргумент функции Ла­пласа Ф(t), отвечающей вероятности Р/2. В данном случае z_р назы­вается квантильным множителем. Половина длины доверительно­го интервала 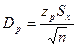называется доверительной границей погрешности результата измерений.

• центр распределения;

• начальные и центральные моменты и производные от них ко­эффициенты – математическое ожидание (МО), Среднее квадратическое отклонение(СКО), эксцесс, контрэксцесс и коэффициент асимметрии.

Понятие центра распределения. Координата центра распределения показывает положение слу­чайной величины на числовой оси и может быть найдена несколь­кими способами. Наиболее фундаментальным является центр сим­метрии, т.е. нахождение такой точки Х_м на оси х, слева и справа от которой вероятности появления различных значений случай­ной величины одинаковы и равны 0,5:

 

 

Точку Х_м называют медианой или 50%-ным квантилем. Для ее нахождения у распределения случайной величины должен сущест­вовать только нулевой начальный момент.

Можно определить центр распределения как центр тяжести рас­пределения, т.е. такой точки , относительно которой опрокиды­вающий момент геометрической фигуры, огибающей которой яв­ляется кривая р(х), равен нулю:

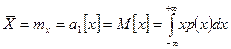
Эта точка называется математическим ожиданием. При симметричной кривой р(х) в качестве центра может ис­пользоваться абсцисса моды, т.е. максимума распределения Х_м. Однако существуют распределения, у которых нет моды, например равномерное. Распределения с одним максимумом называются одномодальными, с двумя – двухмодалъными и т.д. Те из них, у которых в средней части расположен не максимум, а минимум, называются антимодальными.

Для двухмодалъных распределений применяется оценка цен­тра в виде центра сгибов:

,

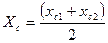где х_с1, х_с2 – сгибы, т.е. абсциссы точек, в которых распределение достигает своих максимумов.

Для ограниченных распределений (равномерного, трапецеи­дального и др.) применяется оценка в виде центра размаха:

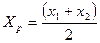
где х₁, х₂ – первый и последний члены вариационного ряда, соот­ветствующего распределению.

Разные оценки центра имеют различную эффективность. При статистической обработке экспериментальных данных важно ис­пользовать наиболее эффективную из них, т.е. оценку, имеющую минимальную дисперсию. Это связано с тем, что погрешность в оп­ределении Х_ц влечет за собой неправильную оценку СКО, границ доверительного интервала, эксцесса, контрэксцесса, вида распреде­ления и др., т.е. всех последующих оценок, кроме энтропийных.