Таблица 1 Таблица 2
| №№измерений | Результаты измерений S i, м | №№измерений | Результаты измерений b i, м | Веса измерений Рi | |
| 13.14 | 
| 1.0 | |||
| .15 | 
| 1.0 | |||
| .16 | 
| 2.0 | |||
| .18 | 
| 2.0 | |||
| .18 | 
| 1.0 | |||
| .15 |
| 1.0 |
Вариант 2
Решение задач по теории ошибок измерений.
Задача 1. По данным ряда случайных ошибок измерений вычислить показатели точности измерений и проверить выполнение свойств случайных ошибок (n =20):
1.09;-2.04;0.93;-0.07;-1.81;0.20;-0.71;1.58;-0.33;-2.18;0.98;0.45;-0.47;-0.13;1.01;0.66;-1.61;-0.88;0.15;-0.86
Задача 2.1. Напишите выражение для средней квадратической погрешности функции 
,
если известна ковариационная матрица её аргументов 
.
Задача 2.2. С какой средней квадратической погрешностью будет определено увеличение трубы 
, если fоб = 250мм иfок =10мм – фокусные расстояния объектива и окуляра, соответственно, определённые независимо со средней квадратической погрешностью 
мм?
Задача 2.3. Дирекционный угол первой линии теодолитного хода получен как среднее арифметическое по результатам определений через два примычных угла (рис.1) 
.Определить среднюю квадратическую погрешность окончательного значения дирекционного угла первой линии 
, если примычные углы измерены независимо со средними квадратическими погрешностями 
, а исходные дирекционные углы 
имеют ковариационную матрицу
. 
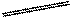
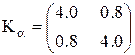Рис.1
Задача 2.4. С какой точностью следует измерить базисы b 1 = 100.00 м и b2 = 110.00 м (угол между ними 
), чтобы определить расстояние S со средней квадратической погрешностью 2 см (рис.2)?
Задача 2.5. С какой точностью будет получено превышение 
, если расстояние S = 50.00 м и угол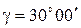 
измерены со средними квадратическими погрешностями ms = 2.0 см, 
?
Задача 3.1. Угол измерен трижды со средней квадратической погрешностью измерений 
. Определить среднюю квадратическую погрешность и вес наиболее надёжного значения угла, приняв 
Задача 3.2. Выразить обратный вес функции 
независимо измеренных аргументов, характеризующиеся весами Р1, Р2, Р3.
Задача 3.3. Высота сигнала h определена по формул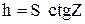е 
, где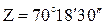 
- зенитное расстояние; S = 124.18 м – расстояние до сигнала. Средние квадратические погрешности измерений 
. Определить вес величины h, приняв ошибку единицы веса 
.
Задача 3.4. Нивелирный ход состоит из четырех секций, превышения в которых измерены со средними квадратическими погрешностями m1 = 6.0 мм, m2 = 4.0 мм, m3 = 6.0 мм, m4 = 2.0 мм. Установить веса измеренных превышений.
Задача 3.5. Вес суммы шести углов равен 2. Измерения равноточные. Определить вес одного угла.
Задача 4. Выполнить математическую обработку рядов равноточных и неравноточных измерений линии S иугла b по данным Таблиц 1 и 2.
Таблица 1 Таблица 2
| №№измерений i | Результаты измерений S i, м | №№измерений i | Результаты измерений b i, м | Веса измерений Рi | |
| 26.11 | 
| 2.0 | |||
| .12 | 
| 2.0 | |||
| .10 | 
| 1.0 | |||
| .15 | 
| 1.0 | |||
| .09 | 
| 2.0 | |||
| .10 | 
| 1.0 |
Вариант 3
Решение задач по теории ошибок измерений.
Задача 1. По данным ряда случайных ошибок измерений вычислить показатели точности измерений и проверить выполнение свойств случайных ошибок (n =20):
0.98;0.45;-0.47;-0.13;1.01;0.66;-1.61;-0.88;0.15;-0.86;-0.28;0.23;1.16;-0.13;-0.88;1.05;0.03;0.12;-1.45;0.85
Задача 2.1. Напишите выражение для средней квадратической погрешности функции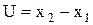 
. Ковариационная матрица аргументов равна 
.
Задача 2.2. Объем тела вычисляется по формуле 
.Высота тела h = 2.00 м определена со средней квадратической погрешностью 
. 
- площади верхнего и нижнего оснований, определённые со средними квадратическими погрешностями 
Найти среднюю квадратическую погрешность объема тела V.
Задача 2.3. С какой средней квадратической погрешностью будет определено место нуля теодолита, если отсчеты КП и КЛ характеризуются средней квадратической погрешностью 
?
Задача 2.4. С какой точностью будет определено расстояние 
,если базисы b1 = 100.00 м и b2 = 110.00 м характеризуются средней квадратической погрешностью mb= 2.0 см, а угол между ними 
- средней квадратической погрешностью 
?
Задача 2.5. Вычислить среднюю квадратическую погрешность дирекционного угла пятой стороны теодолитного хода, если средняя квадратическая погрешность начального дирекционного угла 
, а углы хода характеризуются средней квадратической погрешностью 
?
Задача 3.1. Линия измерена равноточно пять раз. Найти вес среднего арифметического этих измерений, если вес однократногого измерения принят равным 1.
Задача 3.2. Написать выражение для обратного веса функции независимо измеренных аргументов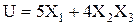 
, если установлены веса аргументов: 
.
Задача 3.3. Угол измерен три раза. Какой вес имеет окончательный результат, если вес одного направления принять равным единице?
Задача 3.4. В треугольнике один угол измерен тремя приемами, второй – шестью. Найти вес вычисленного третьего угла, если все приемы равноточные, а вес угла, полученного из одного приема, принят равным единице.
Задача 3.5. Средняя квадратическая погрешность измерения угла 
. Найти вес суммы 20 углов, измеренных в тех же условиях, если средняя квадратическая погрешность единицы веса 
.
Задача 4. Выполнить математическую обработку рядов равноточных и неравноточных измерений линии S иугла b по данным Таблиц 1 и 2.
Таблица 1 Таблица 2
| №№измерений i | Результаты измерений S i, м | №№измерений i | Результаты измерений b i, м | Веса измерений Рi | |
| 39.21 | 
| 3.0 | |||
| .20 | 
| 2.0 | |||
| .19 | 
| 1.0 | |||
| .18 |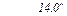 
| 1.0 | |||
| .09 | 
| 1.0 | |||
| .15 | 
| 3.0 |
Вариант 4
Решение задач по теории ошибок измерений.
Задача 1. По данным ряда случайных ошибок измерений вычислить показатели точности измерений и проверить выполнение свойств случайных ошибок (n =20):
-0.28;0.23;1.16;-0.13;-0.88;1.05;0.03;0.12;-1.45;0.85;-0.76;-1.27;-1.44;-0.43;-0.99;-0.68;-0.40;0.10;-2.46;0.58
Задача 2.1. Напишите выражение для средней квадратической погрешности функции 
, если ковариационная матрица её аргументов 
.
Задача 2.2. Определить среднее квадратическое значение угловой невязки многоугольника, если средняя квадратическая погрешность углов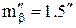 
, а число углов 
.
Задача 2.3. Какова средняя квадратическая погрешность длины линии, вычисленной по приращениям координат 
ковариационная матрица которых равна
(см2).
Задача 2.4. Угол 
в треугольнике вычислен по углам 
и 
, каждый из которых получен дважды со средней квадратической погрешностью однократного измерения 
. Определить среднюю квадратическую погрешность угла .
Задача 2.5. С какой точностью будет вычислена площадь треугольника 
, если его стороны и угол равны: а = 200.00 м, b = 300.00м, 
?. Средние квадратические погрешности независимо измеренных аргументов равны: 
.
Задача 3.1. Измерение, характеризующееся средней квадратической погрешностью 
, имеет вес 
. Определить вес измерения со средней квадратической погрешностью 
.
Задача 3.2. Записать выражение для обратного веса функции 
независимо измеренных аргументов, веса которых равны: 
.
Задача 3.3. Угол получен как среднее из результатов измерений 16 приемами, характеризующимися средней квадратической погрешностью одного приема 
. Угол измерен 9 приемами. Средняя квадратическая погрешность измерений одним приемом 
. Определить вес суммы наиболее надёжных значений углов 
и 
, приняв за ошибку единицы веса 
.
Задача 3.4. Определить вес объема прямоугольного параллелепипеда, если его ребра 
измерены с весами Pa = 8, Pb = 10, Pc = 12.
Задача 3.5. Вычислить вес угла , равного полусумме углов и , веса которых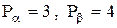 
.
Задача 4. Выполнить математическую обработку рядов равноточных и неравноточных измерений линии S иугла b по данным Таблиц 1 и 2.
Таблица 1 Таблица 2
| №№измерений i | Результаты измерений S i, м | №№измерений i | Результаты измерений b i, м | Веса измерений Рi | |
| 44.12 | 
| 1.0 | |||
| .13 |
| 1.0 | |||
| .10 |
| 2.0 | |||
| .11 |
| 2.0 | |||
| .14 |
| 1.0 | |||
| .10 |
| 1.0 |
Вариант 5
Решение задач по теории ошибок измерений.
Задача 1. По данным ряда случайных ошибок измерений вычислить показатели точности измерений и проверить выполнение свойств случайных ошибок (n =20):
-0.76;-1.27;-1.44;-0.43;-0.99;-0.68;-0.40;0.10;-2.46;0.58;-0.80;-0.52;0.28;0.48;1.28;0.19;-1.83;-0.44;0.36;-0.62
Задача 2.1. Напишите выражение для средней квадратической погрешности функции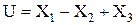 
, если ковариационная матрица её аргументов равна: 
.
Задача 2.2. Определить среднюю квадратическую погрешность уклона воды в реке, вычисляемого по формуле 
, если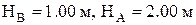 
- отметки уреза воды около кольев, определены со средними квадратическими погрешностями 
, а расстояние между ними 
характеризуется 
Задача 2.3. С какой точностью определена длина линии АВ из решения обратной геодезической задачи, если приращения координат концов линии равны 
. Они характеризуются ковариационной матрицей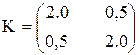 
(см2).
Задача 2.4. Вычислить среднее квадратическое значение невязки приращений абсцисс замкнутого полигона из четырех пунктов. Ковариационная матрица приращений 
(см2).
Задача 2.5. Площадь фигуры состоит из трех частей. С какой точностью должна быть измерена каждая из этих частей, чтобы площадь всей фигуры имела среднюю квадратическую ошибку m = 5 см2?
Задача 3.1. Вес измеренного угла принят равным 9.0. Найти среднюю квадратическую погрешность этого угла, если ошибка единицы веса 
Задача 3.2. Выразить обратный вес функции 
независимо измеренных аргументов, веса которых равны: P1 = 2; P2 = 4; P3 = 3.
Задача 3.3. Углы треугольника измерялись тремя различными теодолитами. Первый угол был измерен 9 раз. Второй – 16 раз, третий – 25 раз. Средние квадратические погрешности измерений для каждого из теодолитов равны, соответственно, 
Найти веса средних значений каждого угла, если ошибка единицы веса 
Задача 3.4.Найти вес полусуммы углов и, если вес каждого из этих углов равен 5.0.
Задача 3.5. Вес измерений угла принят за 1.0. Сколько раз нужно измерить угол, чтобы получить вес окончательного значения равным 4.0?
Задача 4. Выполнить математическую обработку рядов равноточных и неравноточных измерений линии S иугла b по данным Таблиц 1 и 2.
Таблица 1 Таблица 2
| №№измерений i | Результаты измерений S i, м | №№измерений i | Результаты измерений b i, м | Веса измерений Рi | |
| 59.21 | 
| 1.0 | |||
| .31 | 
| 2.0 | |||
| .25 |
| 1.0 | |||
| .26 |
| 2.0 | |||
| .20 | 
| 2.0 | |||
| .25 |
| 1.0 |
Вариант 6
Решение задач по теории ошибок измерений.
Задача 1. По данным ряда случайных ошибок измерений вычислить показатели точности измерений и проверить выполнение свойств случайных ошибок (n =20):
0.80;-0.52;0.28;0.48;1.28;0.19;-1.83;-0.44;0.36;-0.62;-0.12;-0.85;-1.18;0.13;-0.94;-0.36;-0.84;-1.32;-1.39;-0.29.
Задача 2.1. Напишите выражение для средней квадратической погрешности функции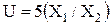 
, если ковариационная матрица её аргументов равна 
.
Задача 2.2. С какой точностью будет получено значение дирекционного угла шестой линии висячего полигонометрического хода, если средняя квадратическая погрешность дирекционного угла примычной стороны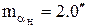 
, а углы характеризуются средней квадратической ошибкой 
?
Задача 2.3. Расстояние S определено по формуле 
, где 
. Средние квадратические погрешности координат и дирекционного угла равны: 
. Определить среднюю квадратическую и относительную погрешности расстояния S.
Задача 2.4. С какой точностью нужно измерить на местности длину линии D = 125 м и угол наклона 
, чтобы получить горизонтальное проложение S со средней квадратической погрешностью 
см?
Задача 2.5. Определить среднее квадратическое значение невязки периметра замкнутого полигона, если известна ковариационная матрица невязок 
по осям координат 
(см2).
Задача 3.1. Средняя квадратическая погрешность измерения угла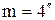 
, его вес Р = 3. Определить среднюю квадратическую погрешность единицы веса.
Задача 3.2. Записать выражение для обратного веса функции 
, если Xi - независимо измеренные аргументы с весами 
.
Задача 3.3. Линия измерена равноточно три раза со средней квадратической погрешностью измерений, равной 
см. Какова средняя квадратическая погрешность и вес окончательного результата, если ошибка единицы веса 
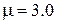см?
Задача 3.4. Определить вес суммы превышений по ходу геометрического нивелирования, состоящему из 4-х станций, если вес отсчета по рейке на станции принять равным 1.0.
Задача 3.5. Один угол треугольника измерен 4 раза со средней квадратической погрешностью измерений 
, второй угол измерен 9 раз со средней квадратической погрешностью 
. Определить среднюю квадратическую погрешность и вес третьего угла, вычисленного по первым двум, принимая за ошибку единицы веса среднюю квадратическую погрешность среднего значения второго угла.
Задача 4. Выполнить математическую обработку рядов равноточных и неравноточных измерений линии S иугла b по данным Таблиц 1 и 2.
Таблица 1 Таблица 2
| №№измерений i | Результаты измерений S i, м | №№измерений i | Результаты измерений b i, м | Веса измерений Рi | |
| 68.31 | 
| 2.0 | |||
| .41 | 
| 1.0 | |||
| .35 |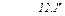 
| 2.0 | |||
| .36 |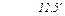 
| 2.0 | |||
| .30 | 
| 1.0 | |||
| .35 | 
| 1.0 |
Вариант 7
Решение задач по теории ошибок измерений.
Задача 1. По данным ряда случайных ошибок измерений вычислить показатели точности измерений и проверить выполнение свойств случайных ошибок (n =20):
-0.12;-0.85;-1.18;0.13;-0.94;-0.36;-0.84;-1.32;-1.39;-0.29;-0.76;-0.27;-1.07;0.60;-0.46;-0.39;-0.87;-1.67;-0.61;0.62
Задача 2.1. Вычислите среднюю квадратическую погрешность функции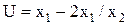 
, если ковариационная матрица её аргументов равна 
. 
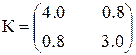Задача 2.2. Вычислить среднее квадратическое значение невязки приращений абсцисс хода, состоящего из четырех сторон, если ковариационная матрица приращений равна:
(см2).
Задача 2.3. Площадь треугольника вычисляется по формуле 
, где а = 60.00 м, b =30.00 м, 
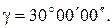Найти среднюю квадратическую погрешность площади, если известны средние квадратические погрешности аргументов: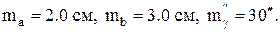 
Задача 2.4. С какой точностью надо измерить углы треугольника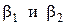 
, чтобы получить значение третьего угла 
со средней квадратической погрешностью 
?
Задача 2.5. Определить среднюю квадратическую погрешность суммы превышений точек нивелирного хода, контролируемую по формуле 
если 
Задание 3.1. Четыре линии полигонометрического хода измерены со средними квадратическими погрешностями 2.0 см, 2.2см, 1.5 см, 1.4 см, углы измерены равноточно и характеризуются средней квадратической погрешностью . Установить веса результатов измерений, приняв 
.
Задача 3.2. Выразить обратный вес функции 
, если 
- независимо измеренные аргументы, веса которых равны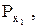 
.
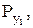
Задача 3.3. Определить вес отметки конечной точки нивелирного хода длиной 16 км, если средняя квадратическая погрешность отметки начальной точки – 18 мм, а превышения по ходу получены со средней квадратической погрешностью 6 мм/км, средняя квадратическая погрешность единицы веса 
мм.
Задача 3.4. В четырехугольнике измерены 3 угла с весами Р1 = 2.0, Р2 =3.0, Р3 =5.0. Определить вес четвертого угла, вычисленного по первым трем.
Задача 3.5. Вес измерений угла принят равным Р =2.0. Сколько измерений нужно сделать, чтобы получить вес окончательного результата с весом Рср = 6.0?
Задача 4. Выполнить математическую обработку рядов равноточных и неравноточных измерений линии S иугла b по данным Таблиц 1 и 2.
Таблица 1 Таблица 2
| №№измерений i | Результаты измерений S i, м | №№измерений i | Результаты измерений Si | Веса измерений Рi | |
| 78.84 | 
| 1.0 | |||
| .80 | 17,2 | 1.0 | |||
| .81 | 18.1 | 2.0 | |||
| .85 | 18.2 | 2.0 | |||
| .80 | 19.0 | 1.0 | |||
| .82 | 19.0 | 1.0 |
Вариант 8
Решение задач по теории ошибок измерений.
Задача 1. По данным ряда случайных ошибок измерений вычислить показатели точности измерений и проверить выполнение свойств случайных ошибок (n =20):
-0.76;-0.27;-1.07;0.60;-0.46;-0.39;-0.87;-1.67;-0.61;0.62;0.34;-1.99;0.25;0.21;-1.11;-0.99;0.93;-0.74;0.64;0.28
Задача 2.1. Написать выражение для средней квадратической погрешности функции 
, если аргументы не коррелированы.
Задача 2.2. Линия S1 измерена дважды со средней квадратической погрешностью измерений m1=2.0см, а линия S2 измерена три раза со средней квадратической погрешностью измерений m2 = 4.0 см. Определите средние квадратические погрешности: а) суммы средних значений этих линий; б) их разности.
Задача 2.3. Превышение h вычислено по формуле 
. С какой точностью должны быть измерены расстояние S= 100.00 м и угол наклона 
, если h требуется получить со средней квадратической погрешностью 
мм?
Задача 2.4. Вычислить среднюю квадратическую погрешность суммы приращений ординат хода из двух линий. Длины линий, их средние квадратические погрешности, дирекционные углы и их ковариационная матрица равны:
| S(м) | 250.00 | 300.00 |
| ms(cm) | 1.0 | 1.3 |
| a | 
| 
|
(″)2;
Задача 2.5. Объем параллелепипеда вычислен по формуле 
, где S=50.00м2 – площадь, а h = = 100.00 м – высота. Средние квадратические погрешности площади и высоты равны, mS = 0,2 м2 и mh = 20 см. Определить среднюю квадратическую погрешность объема V.
Задача 3.1. В треугольнике измеренные углы характеризуются средней квадратической погрешностью 
, а измеренные линии – средними квадратическими погрешностями m1 = 2.0 см, m2 = 3.0 см,
m3 = 4.0см. Установить веса результатов измерений, положив .
Задача 3.2. Написать выражение для обратного веса функции 
. Весанезависимо измеренных аргументов равны Р1, Р2, Р3,Р4.
Задача 3.3. Найти среднюю квадратическую погрешность и вес цены деления уровня, определяемой по рейке и вычисляемой по формуле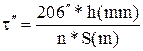 
. Аргументы формулы и их средние квадратические погрешности имеют следующие значения: h=10 мм, mh = 0.50 мм, S= 40.00 м, ms=0.010 м, n=10 делений, mn=0.10 делений. Средняя квадратическая погрешность единицы веса 
.
Задача 3.4. Определить вес горизонтального проложения линии, если её измеренная длина на местности равна S=50.00м. Средняя квадратическая погрешность ms = 0.05 м, вес измеренной длины принят за единицу. Угол наклона 
, средняя квадратическая погрешность угла наклона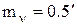 
.
Задача 3.5. Угол наклона измерен 9 раз со средней квадратической погрешностью измерений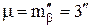 
. Определить среднюю квадратическую погрешность и вес окончательного результата.
Задача 4. Выполнить математическую обработку рядов равноточных и неравноточных измерений линии S иугла b по данным Таблиц 1 и 2.
Таблица 1 Таблица 2
| №№измерений i | Результаты измерений Si | №№измерений i | Результаты измерений Si | Веса измерений Рi | |
| 88.84 | 
| 1.0 | |||
| .80 | 17.2 | 1.0 | |||
| .81 | 18.1 | 2.0 | |||
| .85 | 18.2 | 2.0 | |||
| 19.0 | 1.0 | ||||
| .80 | 19.0 | 1.0 |
Вариант 9
Решение задач по теории ошибок измерений.
Задача 1. По данным ряда случайных ошибок измерений вычислить показатели точности измерений и проверить выполнение свойств случайных ошибок (n =20):
0.47;0.43;-1.05;0.38;-0.99;-0.09;0.21;-0.80;0.52;-0.34;0.26;-0.60;-1.24;0.05;-1.21;-0.62;-0.12;-0.21;1.10;-0.19
Задача 2.1. Написать выражение для средней квадратической погрешности функции 
, если ковариационная матрица её аргументов равна:
.
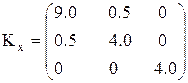Задача 2.2. Для определения высоты дома измерены: базис 
со средней квадратической погрешностью 
и угол 
. со средней квадратической погрешностью 
(см. рис.). Определить среднюю квадратическую погрешность высоты дома а.
Задача 2.3. С какой точностью будет определен диаметр окружности, если средняя квадратическая погрешность радиуса 
Задача 2.4. С какой точностью (СКО) будет определена абсцисса точки К, делящей линию между точками А и В в отношении 
, если 
(cm2).
Напоминаем формулу для вычисления абсциссы искомой точки: 
,
Задача 2.5. С какой точностью должны быть взяты отсчеты КП и КЛ, чтобы место нуля (МО) было вычислено со средней квадратическойпогрешностью 
?
Задача 3.1. Одна и та же линия определена пять раз со средними квадратическими погрешностями результатов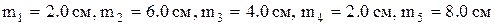 
. Установить веса результатов измерений, положив 
.
Задача 3.2. Написать выражение для обратного веса функции независимо измеренных аргументов 
. Веса аргументов равны Р1, Р2, Р3.
Задача 3.3. Угол измерен 4 раза. Веса результатов измерений равны: 
Средняя квадратическая погрешность единицы веса 
Найти среднюю квадратическую погрешность и вес наиболее надёжного результата.
Задача 3.4. Площадь фигуры состоит из пяти частей, измеренных равноточно. Определить вес площади фигуры, положив веса измеренных частей равными единице.
Задача 3.5. Угол А измерен 4 раза, угол В измерен 9 раз, средняя квадратическая погрешность измерений 
.Определить весаокончательных значений углов А и В, принимая погрешность единицы веса 
Задача 4. Выполнить математическую обработку рядов равноточных и неравноточных измерений линии S иугла b по данным Таблиц 1 и 2.
Таблица 1 Таблица 2
| №№измерений i | Результаты измерений S i, м | №№измерений i | Результаты измерений b i, м | Веса измерений Рi | |
| 59.35 | 
| 1.0 | |||
| .38 | 
| 2.0 | |||
| .41 |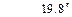 
| 1.0 | |||
| .36 | 
| 2.0 | |||
| .30 |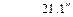 
| 1.0 | |||
| .33 | 
| 1.0 |
Вариант 10
Решение задач по теории ошибок измерений.
Задача 1. По данным ряда случайных ошибок измерений вычислить показатели точности измерений и проверить выполнение свойств случайных ошибок (n =20):
0.23;-0.72;0.68;-0.43;-0.19;-0.81;0.64;0.34;0.62;0.27;0.14;-0.30;-0.28;-0.54;-0.62;-1.20;0.39;-0.11;0.75;0.50
Задача 2.1. Написать выражение для средней квадратической погрешности функции 
, если ковариационная матрица её аргументов равна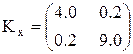 
.
Задача 2.2.. Вычислить среднюю квадратическую погрешность коэффициента нитяного дальномера K=S/ l, где l = 20 см – отсчёт по рейке между дальномерными нитями сетки, характеризующийся средней квадратической погрешностью m l = 1мм, S = 60,00м - расстояние от оси вращения инструмента до рейки, ms = 6см.
Задача 2.3. С какой точностью следует измерить стороны прямоугольника 
, чтобы средняя квадратическая погрешность площади Р равнялась 
Задача 2.4. На местности измерена наклонная линия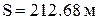 
со средней квадратическойпогрешностью 
и угол наклона к горизонту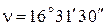 
со средней квадратическойпогрешностью 
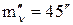. Определить среднюю квадратическую погрешность её горизонтального проложения D.
Задача 2.5. Угол измерен 4 раза со средней квадратическойпогрешностью измерений 
. Определить среднюю квадратическую погрешность наиболее надёжного значения угла.
Задача 3.1. В треугольнике измерены 3 угла со средними квадратическими погрешностями измерений, равными 
Вес первого угла равен 1.0.Чему равны веса второго и третьего углов треугольника?
