Поставить краевую задачу, соответствующую данной физической задаче – это значит выбрать функцию, характеризующую физический процесс и затем:
а) записать дифференциальное уравнение для этой функции;
б) установить для нее граничные условия;
в) сформулировать начальные условия.
Уравнения и граничные условия краевых задач, например, теории теплопроводности, являются следствием:
1) закона сохранения энергии;
2) закона внутренней теплопроводности в твердых телах (закона Фурье), который в одномерном случае выражается следующим образом:
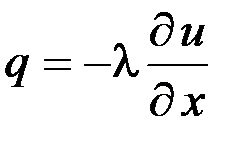 ,
,
где q – количество тепла, протекающего в единицу времени в направлении оси x через единицу площади;
u – температура в рассматриваемом месте тела;
λ – коэффициент теплопроводности, который зависит от физических свойств тела и от температуры u; но при решении данных задач зависимостью λ от температуры пренебрегаем.
3) закона конвективного теплообмена между поверхностью твердого тела и окружающей его газообразной или жидкой средой (закон Ньютона), который выражается формулой
 ,
,
где q – количество тепла, протекающего в единицу времени через единицу площади поверхности тела в окружающую среду;
 – коэффициент теплоотдачи;
– коэффициент теплоотдачи;
u – температура поверхности тела;
θ – температура окружающей среды.
Рассмотрим подробнее, как записываются граничные условия. Они различаются в зависимости от температурного режима на границах рассматриваемой области. Обычно рассматривают три основных типа граничных условий (ограничимся одномерным случаем):
I. Задается температура на поверхности тела. Например, на конце стержня (при x = 0) задана температура
 . (18.7)
. (18.7)
II. Задается поток тепла через поверхности тела (в случае теплоизолированного с боковой поверхности стержня – величина теплового потока, протекающего через торцевое сечение стержня). Например, на концах 
 , (18.8)
, (18.8)
где  – известная функция, выражающаяся через заданный тепловой поток и коэффициент теплопроводности по формуле
– известная функция, выражающаяся через заданный тепловой поток и коэффициент теплопроводности по формуле
 .
.
Если какой либо конец стержня теплоизолирован, то граничное условие примет вид
 . (18.9)
. (18.9)
III. На поверхности тела происходит теплообмен со средой, имеющей температуру  , по закону Ньютона (согласно которому поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды). Математическая формулировка третьего граничного условия (на конце стержня
, по закону Ньютона (согласно которому поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды). Математическая формулировка третьего граничного условия (на конце стержня  ) имеет вид:
) имеет вид:
 , (18.10)
, (18.10)
где  – коэффициент теплоотдачи.
– коэффициент теплоотдачи.
Условия (18.7) – (18.9) также можно рассматривать как частный случай общих условий (18.4).
Поток тепла считается положительным, если тепло уходит из стержня в окружающую среду (u > θ), и отрицательным – в противоположном случае.
Согласно закону сохранения энергии количество уходящего тепла должно быть равно потоку тепла, проходящего через рассматриваемое торцевое сечение в силу теплопроводности стержня.
Пусть начало стержня совпадает с началом координат (x = 0), а конец его имеет абсциссу  . Тепловой поток, проходящий через поперечное сечение стержня в направлении оси 0 x, равен
. Тепловой поток, проходящий через поперечное сечение стержня в направлении оси 0 x, равен  . На правом конце стержня направление потока, поступающего во внешнюю среду, совпадает с направлением оси 0 x, а поток равен
. На правом конце стержня направление потока, поступающего во внешнюю среду, совпадает с направлением оси 0 x, а поток равен  . На левом конце эти направления противоположны и поэтому тепловой поток равен
. На левом конце эти направления противоположны и поэтому тепловой поток равен 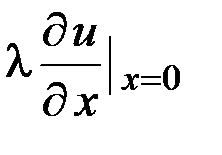 . Будем считать, что внешние среды на концах стержня разные, поэтому могут быть различными
. Будем считать, что внешние среды на концах стержня разные, поэтому могут быть различными  и θ. Пусть на правом конце
и θ. Пусть на правом конце  ,
,  , а на левом
, а на левом  ,
,  . В этом случае граничные условия на торцевых сечениях можно записать в следующем виде
. В этом случае граничные условия на торцевых сечениях можно записать в следующем виде
 ,
,
(18.11)
 ,
,
где  ,
, 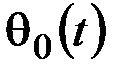 – заданные температуры внешней среды, которые являются известными функциями от времени t.
– заданные температуры внешней среды, которые являются известными функциями от времени t.
Граничные условия на концах стержня (при x = 0 и  ) могут быть различных типов.
) могут быть различных типов.
Кроме описанных выше линейных краевых задач, существуют также задачи с нелинейными граничными условиями, например
 .
.
Это граничное условие соответствует излучению по закону Стефана – Больцмана в среду с температурой  с торца
с торца  .
.
Рассмотрим более подробно, например, задачу (с граничными условиями первого рода) для ограниченной области (стержня длиной 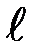 ). Задача состоит в отыскании решения
). Задача состоит в отыскании решения  дифференциального уравнения теплопроводности
дифференциального уравнения теплопроводности
 при 0 < x <
при 0 < x < 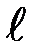 , 0 < t
, 0 < t 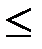 T,
T,
удовлетворяющего начальному и граничному условиям
 , 0 ≤ x ≤
, 0 ≤ x ≤ 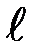 ,
,
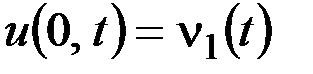 ,
,  , 0 ≤ t
, 0 ≤ t 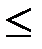 T,
T,
где  ,
,  ,
,  – заданные функции.
– заданные функции.
Аналогично ставятся другие задачи с различными комбинациями граничных условий.






