Многие задачи механики, физики, технологии приводят к исследованию дифференциальных уравнений с частными производными второго порядка, называемых уравнениями математической физики.
Дифференциальные уравнения математической физики,которые мы будем изучать, – это линейные уравнения второго порядка. Как указано ранее уравнение называют линейным, если оно первой степени относительно искомой функции и всех ее производных и не содержит их произведений, то есть если это уравнение может быть записано в виде уравнения (18.1)
Общепринята следующая классификация уравнения (18.1). Принадлежность уравнения к тому или иному типу определяется коэффициентами при старших производных.
Обозначим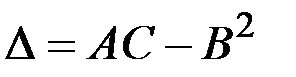 
– дискриминант уравнения. В зависимости от знака функции Δ уравнение (18.1) относится в данной области к одному из следующих типов:
Δ < 0 – гиперболический тип;
Δ = 0 – параболический тип;
Δ > 0 – эллиптический тип;
Δ не сохраняет постоянного знака – смешанный тип.
Замечание. В уравнении (18.1) независимыми переменными являются координаты x и y. Во многих задачах одной из двух независимых переменных является время и уравнение (18.1) можно записать через x и t (см. табл. 1).
Пример.
В уравнении
B = C = 0; Δ = 0 – это уравнение параболического типа.
Пример.
В уравнении Лапласа
–
A = 1, B = 0, C = 1, Δ = AC – B 2 > 0 – это уравнение эллиптического типа.
Пример.
–
уравнение смешанного типа в любой области P, содержащей точки оси 0 X. При y < 0 оно гиперболического типа, при y > 0 – эллиптического типа, при y = 0 – линии параболичности.
Пример.
Докажите самостоятельно, что уравнение
– гиперболического типа.
Краевые условия
Дифференциальные уравнения с частными производными имеют в общем случае бесчисленное множество решений. Поэтому, если физический процесс описывается с помощью уравнения с частными производными, то для однозначной характеристики этого процесса необходимы какие то дополнительные условия. Эти дополнительные данные состоят из краевых, то есть граничных и начальных условий.
Граничные условия заключаются в том, что указываются значения неизвестной функции u на концах промежутка изменения координаты (в задаче о линейной теплопроводности это концы стержня, в задачах о колебаниях струны – это концы струны и т.д.).
Условия, относящиеся к начальному моменту времени, называются начальными.
В каком же случае задаются какие краевые условия? Для того, чтобы лучше понять это, следует рассмотреть понятие стационарного и нестационарного процессов.
Нестационарными называются задачи, решение которых зависит не только от пространственных координат (x, y, z), но и от времени t. Эти задачи связаны с процессами, протекающими во времени. Например, это процессы распространения тепла, процессы диффузии, колебательные (волновые) процессы, процессы распространения электрических волн и ряд других.
Основными дифференциальными уравнениями математической физики, описывающими нестационарные процессы, являются уравнение теплопроводности
(18.2)
и волновое уравнение
(18.3)
Уравнение (18.2) является уравнением параболического типа, а уравнение (18.3) – гиперболического. Постановка задач для уравнений этих типов характеризуется наличием как граничных, так и начальных условий.
Начальные условия состоят в задании в момент времени t = 0 значений искомой функции u и ее производной (в гиперболическом случае) или только значений самой функции (в параболическом случае).
Таким образом, для уравнения теплопроводности ставится одно начальное условие (то есть условие при t = 0)
u =(0, x, y, z) = φ(x, y, z), (18.4)
а для волнового уравнения – два:
u =(0, x, y, z) = φ(x, y, z), (18.5)
(0, x, y, z) = ψ(x, y, z). (18.6)
В случае, если процесс протекает в неограниченной области (область называется неограниченной, если хотя бы одна из координат ее точек может быть сколь угодно большой, например бесконечный стержень, бесконечная струна и т.д.), то задаются лишь начальные условия (задача Коши).
В случае, если задача ставится для конечного интервала, то должны быть заданы и начальные и граничные условия. Тогда говорят о смешанной задаче.
Для описания стационарных процессов обычно используют уравнения эллиптического типа. Время t в эти уравнения не входит. Такими оказываются уравнения стационарного температурного поля, электростатического поля и т.д. Для задач такого типа ставятся только граничные условия, то есть указывается поведение неизвестной функции на контуре области (см.таблицу 1).
В рассматриваемых нами задачах математической физики именно физические соображения подсказывают, какие дополнительные условия следует поставить в той или иной задаче, чтобы получить единственное ее решение, отвечающее характеру изучаемого процесса.
Таблица 1
Важнейшие линейные дифференциальные уравнения математической физики
| Тип | Физический смысл | Одномерное уравнение | Многомерное уравнение | Дополнительные (краевые) условия |
| Гиперболический | Волны (струны, мембраны, течение жидкости) затухающие волны | 
| 
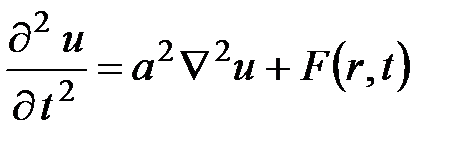
| Граничные условия; начальные условия для u и 
|
| Параболи- ческий | Уравнения теплопроводности, диффузии | 
| 
| Граничные условия; начальное условие для u |
| Эллиптический | Статический случай | 
| 
| Только граничные условия |
– оператор Лапласа.
Например в декартовых координатах
