Пример15.1. Изобразить точками комплексной плоскости комплексные числа 2+3 i, -4+2,5 i, -2,7-3,3 i, 3-2 i.
Решение. Между точками числовой плоскости и множеством комплексных чисел существует взаимно однозначное соответствие
Любому комплексному числу x + iy соответствует только одна точка числовой плоскости, определяемая координатами (x, y), и обратно, любой точке плоскости соответствует только одно комплексное число, действительная часть которого равна абсциссе, а коэффициент при мнимой части – ординате точки.
| -1 -2 -3 |
| -5 -4 -3 -2 -1 |
| D |
| С |
| В |
| А |
| х |
| у |
точка В – комплексное число В = -4+2,5 i;
точка С – комплексное число С =-2,7-3,3 i;
точка D – комплексное число D =3-2 i.
Пример 15.2. Даны два числа в алгебраической форме:
z 1=5 + 7 i; z 2=3-4 i. Найти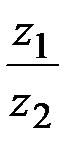 
.
Решение.
.
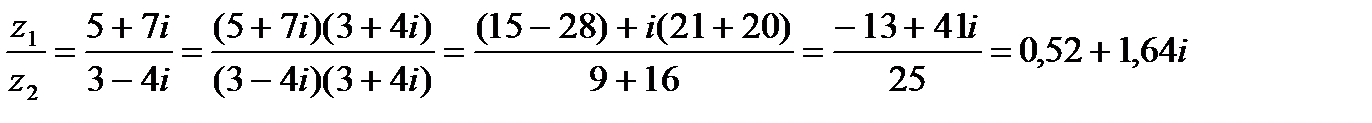Пример15.3. Дано: z 1=10-7 i; z 2=5 i; z 3=3+4 i; z 4=(-1+5 i); z 5=1-3 i. Найти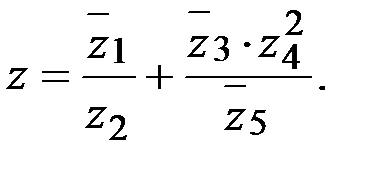 
Решение.
.
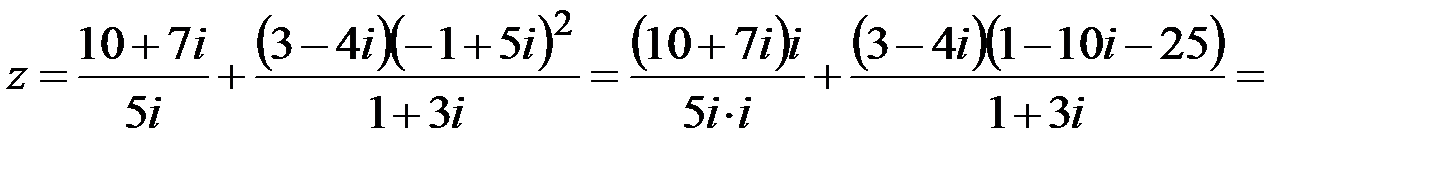
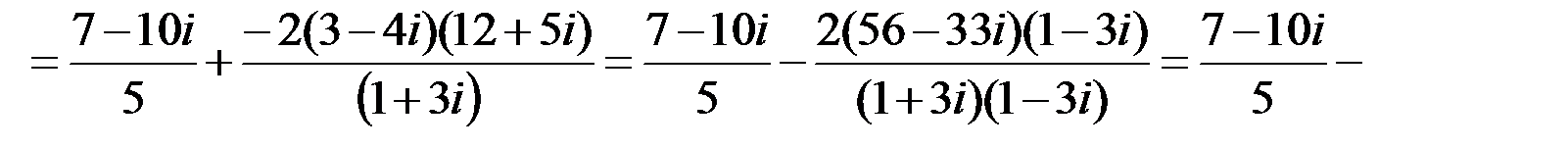
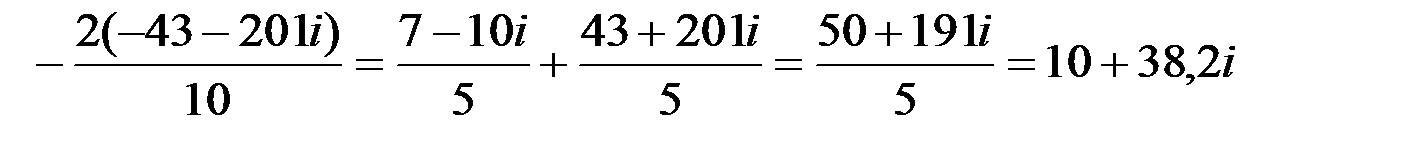Пример 15.4. Даны два числа в тригонометрической форме: z 1=2(cos 
+ i sin ); z 2=5(cos 
+ i sin ). Найти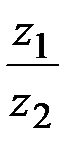 
.
Решение. r 1=2; j1= ; r 2=5; j2= .
Подставим эти значения r 1, r 2, j1 и j2 в формулу (15.11), получим
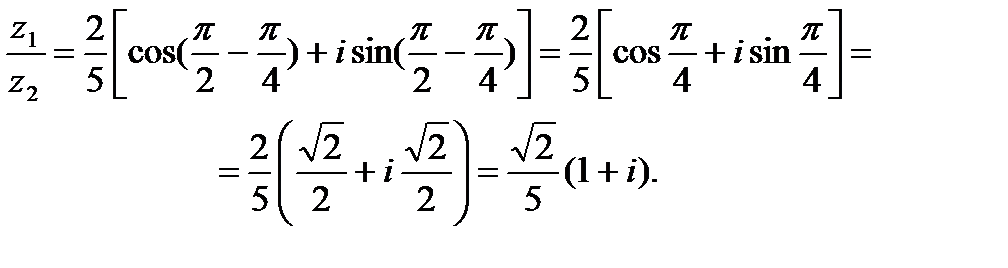
Пример15.5. Заданы комплексные числа: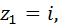 
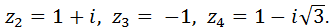Требуется:
1) представить z 1, z 2, z 3 в тригонометрической и показательной форме;
2) вычислить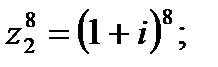 
3) вычислить все значения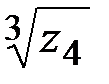 
.
Решение. 1. Чтобы записать комплексное число в тригонометрической или показательной формах, необходимо найти его модуль и аргумент по формулам (15.2) и (15.5):
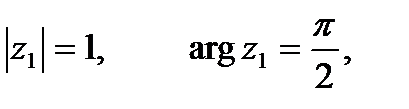
отсюда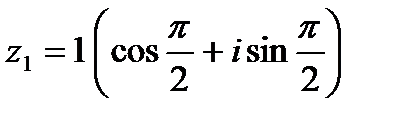 
, 
,
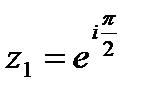т. е.
,
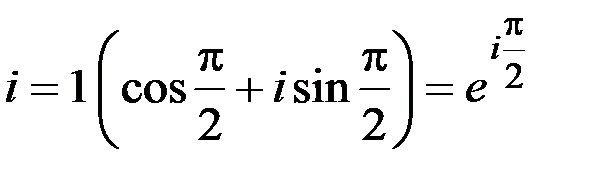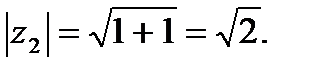
Точка принадлежит первой четверти, поэтому
.
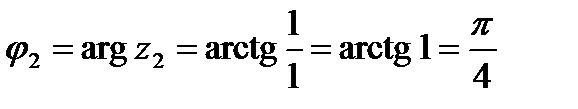Тогда по формуле (15.3)
,
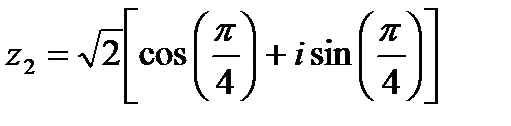а по формуле (15.7)
.
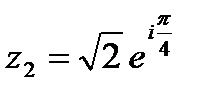Итак,
,
,
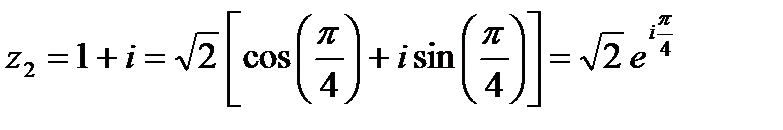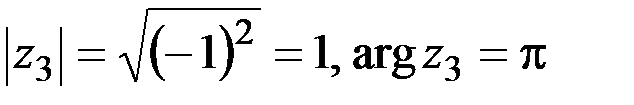поэтому
,
,
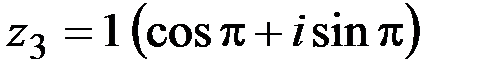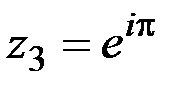т. е.
.
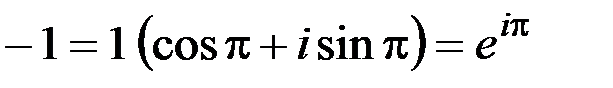2. Воспользуемся тригонометрической формой комплексного числа z 1 и формулой Муавра
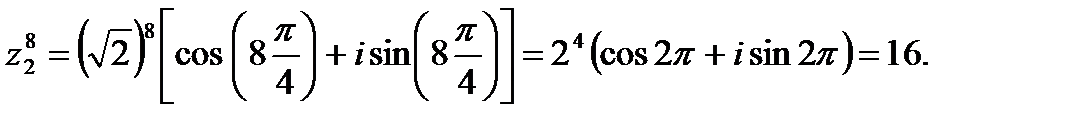
3. Перейдем к тригонометрической форме комплексного числа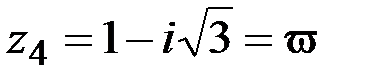 
: 
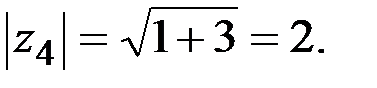Комплексное число z4 лежит в 4-й четверти.
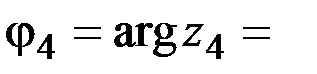arctg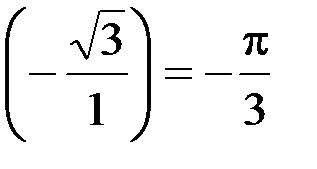 
, так как arctg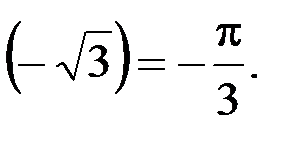 
.
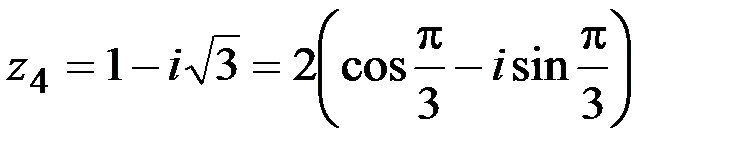Воспользуемся формулой (15.13), где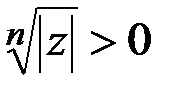 
– арифметический корень:
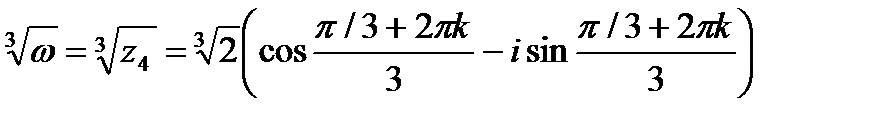, (k =0, 1, 2, …).
при k =0
;
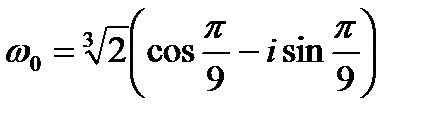при k =1
;
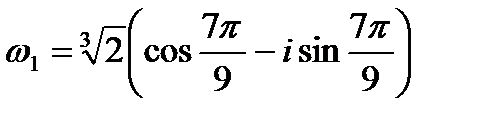при k =2
.
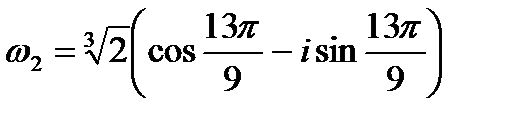Пример15.6. Изобразить в комплексной плоскости линии, заданные следующим образом:
1) 
;
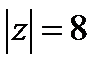2) 
.
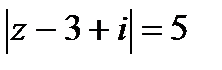Решение. 1. Линия - окружность с центром в начале координат с радиусом, равным 8, так как по определению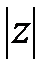 
- это расстояние от начала координат до точки z.
2. 
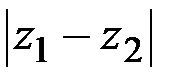– это расстояние между точкам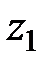и 
и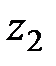 
. Поэтому равенство 
означает, что точки искомой линии удалены на расстояние, равное 5 от точки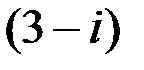 
.
Т.е. искомая линия представляет собой окружность радиусом 5 с центром в точке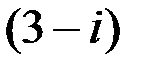 
.
| ç z -3 + i │=5 |
| x |
| -2 |
| -1 |
| -3 |
| y |
| -1 |
| О |
| 7 |
| 3 - i |
Пример 15.7. Указать геометрические места точек комплексной плоскости, для которых выполняются следующие условия:
1) 
;
2) 
;
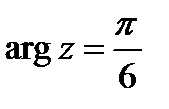3) 
;
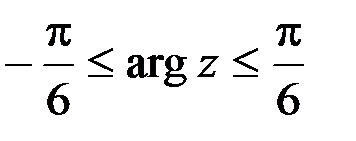4) 
.
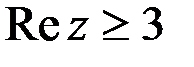Решение. 1.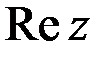 
означает действительную часть комплексного числа 
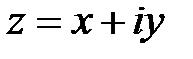, т. е. 
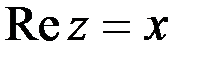. Поэтому вместо уравнения 
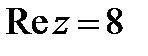можно написать 
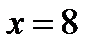. Это уравнение прямой, параллельной оси ординат.
2. Уравнению 
удовлетворяет множество точек, находящихся на луче, выходящем из начала координат, который образует с осью абсцисс угол 30°.
3. Искомое множество представляет из себя угол, ограниченный лучам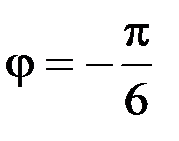и 
и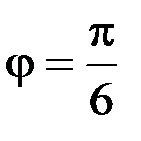 
,
|
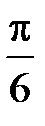
| x |
| y |
|
|
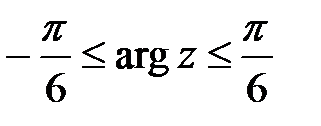
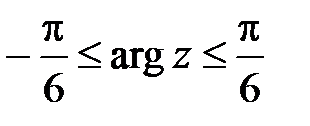
| О |
4. Действительная часть комплексного числа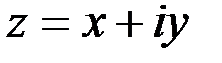 
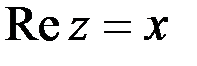. Следовательно, данное множество – правая полуплоскость
| y |
| x |
| O |
| Re z ≥ 3 |
Пример 15.8. Дано w = z 2, где z = x + i y. Найти Re w и Im w.
Решение.
w =(x + i y)2 = x 2 + 2 x i y + i 2 y 2 =
x 3 + 2 x i y – y 2 =
= (x 2 - y 2) + 2 x y i.
Отсюда
Re z 2 = u (x, y) = x 2 - y 2 Im z2 = υ (x, y) = 2 x y.
Пример 15.9. Изобразить на комплексной плоскости области, заданные следующими неравенствами, и установить, являются ли они односвязными.
1) 
;
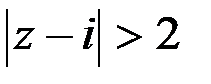2) 
.
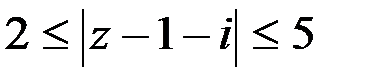| x |
| y |
| О |
| R |
| z 0 |
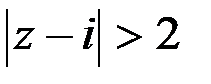удовлетворяют точки вне круга радиусом 2 с центром в точке 
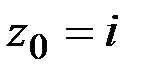, за исключением его границы, уравнение которой 
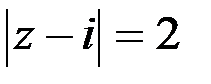. Это односвязная область.
x
О
y
i
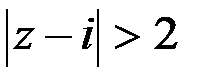
2)Условию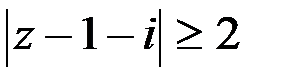 
удовлетворяют точки вне круга с центром в точке 
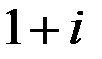радиусом 2 и условию 
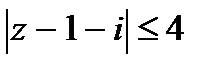- круг радиуса 4 с центром в той же точке 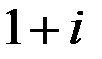. Следовательно, данное множество представляет из себя кольцо, ограниченное окружностями радиусов 2 и 4 с центром в точке 
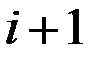. Это двусвязная область.
| y |
| x |
| 1 |
| - 2 |
| - 3 |
| - 1 |
| 1 + i |
| i |
| 2£½ z -1- i ½£4 |
Пример 15.10. Найти производную функции e 5 iz +7 и показать, что она дифференцируема при любом значении z.
Решение. функции ez и 5 iz+ 7 дифференцируемы при всех значениях z. Поэтому и сложная функция, составленная из них, также дифференцируема:
(e 5 iz+ 7)' = e 5 iz+ 7 (5 iz+ 7)' = 5 i e 5 iz+ 7.
Пример 15.11. Найти все особые точки следующей функции, определить их характер:
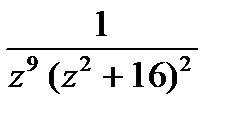
Решение. Так как функция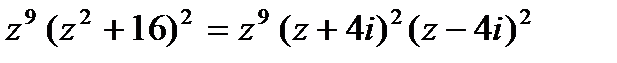 
имеет три нуля: 
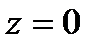– девятого порядка; 
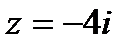и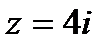 
– второго порядка, то функция 
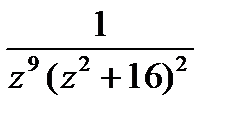имеет три полюса: в точке 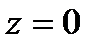– девятого порядка; 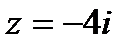и 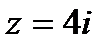– второго порядка.
